A.G.a.Fe
(Algebraic Geometry at Ferrara)
Fagnano e gli archi di lemniscata
Gli studi di Giulio de Toschi conte di Fagnano (1682–1766), riguardanti la lunghezza dell’arco
di lemniscata, ossia della curva piana di equazione:
ove a > 0 (in coordinate
polari 
) risalgono al 1716. L’interesse per questa curva risale però a Jakob Bernoulli [Curvatura
Laminae Elasticae, Acta Eruditorum 13, 207–276 (1694)] e prima
ancora a Giovanni
Domenico Cassini
(1625–1712). Bernoulli in Costructio curvae acessus et recessus aequabilis,
ope rectificationis curvae cujusdam algebraicae: addenda nuperae solutioni mensis junii, descriveva la
curva “fatta come un otto, o un nodo,
o l’anello di un nastro” [Acta Eruditorum 1694]. La curva lemniscata, è
un caso speciale di “ovale di Cassini”: luogo dei punti del piano per i quali il prodotto delle loro
distanze da due punti fissi (detti fuochi) è
costante. Nel caso in cui il punto medio dei fuochi appartiene al luogo si
ottiene la lemniscata di Bernoulli. Legendre,
nell’introduzione al Traité des fonctions elliptiques [1825–27,
vol.1, pag. 2], riferendosi
a Fagnano, scrive :
...mais les différens résultats
[sulle quadrature] n’étaient point liés entre eux et
ne pouvaient former alcune théorie. Un Géomètre italien d’une grande sagacité,
ouvrit la route à des spéculations plus profondes
...Ma
i diversi risultati [sulle quadrature] non erano legati tra loro e non potevano
formare alcuna teoria. Un Geometra italiano di una grande sagacità, aprì la via
a speculazioni più profonde.
Precisamente le lemniscate sono definite
geometricamente come il luogo dei punti P
del piano tali che il prodotto delle distanze 
da due punti fissati 
è una costante c2 .
Riferito il piano ad un sistema di assi cartesiani ortogonali posto 
dette rispettivamente 
,
le distante di P = (x, y) dall’origine O = (0, 0), di P da B1 e di P
da B2 si ha: 
, 
e 
.
Posto 
dopo qualche semplice calcolo
algebrico si ottiene che:
,
da cui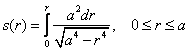 
che esprime la lunghezza di un
arco di lemniscata nel primo quadrante.
Al Metodo per misurare la lemniscata, Fagnano dedicò tre note che apparvero nel Giornale de letterati d’Italia, tomi
XXIX, XXX, XXXIV [vedi anche Produzioni Matematiche
vol. II, pp. 343–360]. Nella nota Teorema da cui si deduce una
nuova misura degli archi ellittici, iperbolici e cicloidali [Giornale de letterati d’Italia, tomo XXVI,
Produzioni Matematiche, pp. 287–292]
, Fagnano provò che la differenza di archi di una
stessa ellisse, o di una stessa iperbole o di una stessa cicloide, sono
espressioni algebriche delle variabili coinvolte. Da questi risultati si deduce
che, sebbene gli archi (di ellisse, di iperbole o di cicloide) siano funzioni
trascendenti delle variabili, particolari combinazioni di essi sono funzioni
algebriche delle stesse. Questa osservazione contiene il germe del famoso
teorema di Abel sulle funzioni trascendenti (1826).
La nota di maggior interesse è Metodo per misurare la lemniscata, Schediasma II
(1718). Qui, Fagnano proseguì lo studio degli archi
di lemniscata, con a = 1. In particolare dimostrò che:
quando 
, ottenendo la formula di
duplicazione dell’arco di lemniscata.
Nei problemi I e II della memoria sopra ricordata, Fagnano
ottenne anche la divisione in tre e in cinque parti uguali del primo quadrante
di lemniscata (arco corrispondente al primo quadrante
coordinato) e concluse con il seguente corollario:
...il
quadrante della lemniscata potrà dividersi
algebricamente in tante parti uguali, quanti numeri si contengono in queste tre
formule, e cioè
, nelle quali l’esponente m significa qualunque
numero intero positivo. E questa è una nuova, e singolare proprietà della mia
curva.
Legendre nel suo Traité des
fonctions elliptiques, commentò così l’opera del
Fagnano:
... Il prouva que
sur toute les ellipse ou sur toute hyperbole domné,
on peut assigner, d’une infinité de manières, deux arcs dont la différence soit
égale à une quantité algébrique. Il démontra en même temps que la courbe nommée
lemniscate jouit de cette singulière propriété, que ses arcs peuvent être
multipliés ou divisés algebriquement, comme arcs de
cercle...
... Egli prova che su tutte le ellissi o su tutte le iperboli, si possono assegnare, in una infinità di modi, due archi la cui differenza sia uguale ad una quantità algebrica. Egli dimostra nello stesso tempo, che la curva nominata ”lemniscata” soddisfa questa proprietà singolare, che i suoi archi possono essere moltiplicati o divisi algebricamente, come archi di cerchio.