A.G.a.Fe
(Algebraic Geometry at Ferrara)
Euler e il Teorema di Addizione
|
|
I risultati di Fagnano rimasero pressoché sconosciuti finché Euler non ne venne a conoscenza il 23 Dicembre del 1751,
quando l’accademia delle Scienze di Berlino dovendo decidere la nomina di Fagnano a membro corrispondente conferì Euler l’incarico di leggerne le opere. Egli, che era
molto interessato alle quadrature legate ai problemi di meccanica e di teoria
delle lamine elastiche (dunque in particolare alla quadratura della lemniscata), non tardò a comprendere l’importanza dei
risultati di Fagnano e, soprattutto, quali sviluppi
avrebbero potuto avere [lettera a Goldbach del 19–30 Maggio 1752, Briefwechsel,
ed. Juskevic e Winter,
1965]. Molti anni più tardi, Karl
Gustav Jakob Jacobi (1804–1851), come appare da una sua lettera a Nicolaus Von
Fuss (1755–1826) considerò il 23 Dicembre del
1751 la data di nascita della teoria delle funzioni ellittiche [P. Stäckel, W. Ahrens,
Der briefwechsel zwischen C. G. J. Jacobi und P.H. von Fuss
über die Herausgabe der Werke Leonard
Euler, Leipzig 1908].
La prima memoria importante su tale argomento è il De Integratione aequationis differentialis Scientiarum Imperialis Petropolitanae 6 (1761), 35–57; Opera
Omnia, I, 20, pp. 58–79]. |
Qui,
Euler prese come punto di partenza i risultati di Fagnano e considerando l’equazione:
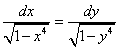(1)
scrisse:
Cum primum occasione inuentionum Ill.
Comitis Fagnani hanc aequationem effem contemplatus, eiusmodi quidem relationem algebraicam inter variabiles x et y elicui, quae huic aequationi
fatisfaceret; fed ea relatio non pro aequatione integrali completa haberi
poterat, propterea quod non complecteretur quantitatem conflatem arbitrariam, cuiusmodi femper in calculum per integrationem introduci folet. Hinc enim, vti
fatis notum eft, integralia incompleta et particularia diftingui folent, quorum illa totam vim
aequationum differentialium
exhauriunt, haec vero
tantum ita fatisfaciunt, vt aliae infuper
expreffiones aeque fatisfacere queant. Criterium autem aequationis integralis completae in hoc confiftit, quod ea quantitatem conflantem inuoluere debeat, quae in aequatione defferentiali non apparet.
Quando, sollecitato dalla scoperta
dell’Illustrissimo Conte Fagnano, ho considerato
questa equazione, ho cercato una relazione algebrica tra le variabili x e y che
soddisfacesse l’equazione: ma questa relazione non poteva avere la forma di un
integrale completo, poiché non conteneva una quantità costante arbitraria, come
è solito essere introdotta nel calcolo dall’integrazione. Dunque, come è ben
noto, si è soliti distinguere tra integrali completi e particolari, del quale
il primo esaurisce l’intera forza dell’equazione differenziale, mentre il
secondo, certamente, la soddisfa ma ci sono altre espressioni, oltre a questa,
che la soddisfano ugualmente. Perciò, il criterio per determinare un integrale
completo consiste in questo: si deve introdurre una quantità costante che non
appare nell’equazione differenziale.
Più avanti:
Saepe
numero autem aequationis differentialis integrale particulare
algebraicum exhibiri poteft, cum tamen
integrale completum fit trafcendes; hoc fcilicet euenit, fi pars tranfcendens per conftantem illam arbitrariam fuerit multiplicata, quae propterea, conftante illa nihilo aequali pofita, ex calculo euanefcit, et integrale algebraicum particulare relinquit.
Spesso è possibile dare un integrale algebrico
particolare per un’equazione differenziale, anche se l’integrale completo è
trascendente; questo comporta evidentemente che, se la parte trascendente è
moltiplicata per una costante arbitraria, in modo tale che se la costante è
posta uguale a 0, la parte trascendente si annullerà e
rimarrà un integrale algebrico particolare.
Euler, decise allora di cercare gli integrali
generali sotto forma algebrica partendo dalla (1), ma con l’intenzione di
ottenere l’integrale generale dell’equazione:
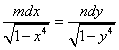(2)
che esprime il problema di
trovare due archi di lemniscata tali che le loro lunghezze abbiano rapporto 
. Euler, indotto da successivi tentativi è sicuro
che la (2) ha un integrale generale esprimibile algebricamente quando
è razionale.
Dalle ricerche di Fagnano si ricava che
l’equazione (1) è soddisfatta dall’integrale particolare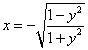 
o equivalentemente
.
L’integrale di ciascun membro della (1) è un arco di lemniscata di semiasse 1 e ascissa x e l’integrazione
dell’equazione differenziale (1) equivale a trovare due archi
di lunghezza uguale. Euler aveva osservato che x = y è un altro integrale particolare della (1).
L’integrale generale doveva perciò
essere tale da ridursi a ciascuno di questi integrali particolari per valori
speciali delle costanti arbitrarie. Guidato da questi fatti, Euler enunciò il seguente teorema:
Teorema: Io dico dunque che
l’integrale completo di questa equazione differenziale
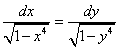
è
.
Da qui Euler ottenne il teorema di
addizione per gli archi di lemniscata (nel primo
quadrante):
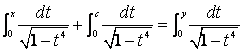
dove 
. Notiamo che se c = x, questa formula
coincide con la formula di duplicazione di Fagnano.
Conviene ora ricordare la formula di addizione per la funzione sin z:
sin(u + v) = sin u cos v + cos u sin v.
Questa formula si traduce per gli integrali circolari 
nella seguente formula
di addizione:
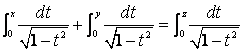
dove, posto x = sin u, y = sin v si ha 
(supponendo x, y > 0 e molto vicini a 0). La determinazione dell’integrale generale
dell’equazione differenziale 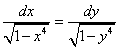, e
l’applicazione al teorema di addizione per gli archi di lemniscata,
fu la prima scoperta di Euler
nell’ambito degli integrali ellittici.
Nella memoria Observationes De Comparatione Arcuum Irrectificabilium, [Novi Commentari Academiae Scientiarum Imperialis Petropolitanae, Tomo 6
(1756/7), 1761, pp. 58–84, Opera Omnia, Serie I, Vol. 20, pp. 81–107], Euler intraprese lo studio delle quadrature e delle
relazioni tra esse, utilizzando i risultati precedenti. Euler
presenta infatti teoremi sugli archi di ellisse, iperbole e lemniscata
le cui cordinate sono la somma o la differenza di una
qualche funzione algebrica, o di archi che sono multipli di altri. Qui ritrova,
ed estende, i risultati di Fagnano, ed in particolare
dimostra il teorema di divisione in 2n(1+2n) parti dell’arco di lemniscata.
Euler dedicò altre memorie allo studio delle
equazioni differenziali. Nella Memoria Speciem
alterum methodi novae quantitatis trascendentes inter se comparandi
de comparatione arcuum Ellipsis [Novi
Commentari Academiae Scientiarum
Petropolitanae, 7 (1758/9, 1761, pp. 3–48; Opera
Omnia, Serie I, Vol.
20, pp. 153–200)], egli ottenne
che anche l’equazione differenziale:
(con 
) è integrabile algebricamente, con integrale generale della
forma 
dove c è una costante arbitraria. Dunque il teorema di
addizione per gli integrali del tipo
è espresso da:
dove 
. Infine Euler si occupò
dell’equazione: 
con P(x) = A + 2Bx + Cx2 + 2Dx3 + Ex4 nella memoria Integratio
aequationis 
[Novi
Commentari Academiae Scientiarum
Imperialis
Petropolitanae, 12, (1766/7), 1768, pp. 3–16; Opera Omnia,Serie I, Vol.
20, pp. 302–317]. Tuttavia, nonostante l’importanza delle sue scoperte, Euler si rammaricò che i suoi metodi non fossero
estendibili a radici superiori a quella quadrata o a radicandi di grado
superiore al quarto. Vedeva anche un grave difetto nelle sue ricerche per il
fatto che, l’integrazione delle equazioni differenziali da lui effettuata, non
seguisse un metodo preciso, ma fosse “potius tentando vel divinando”, e auspicava la ricerca di un metodo
diretto e generale, cosicché i suoi risultati potessero avere una relazione
naturale con le altre parti del calcolo infinitesimale.
Nel 1767 Joseph
Louis Lagrange
(1736–1813) rispose all’esortazione euleriana
ottenendo quanto trovato da Euler con un metodo
generale, la cui applicazione si eleva dalle trascendenti più semplici a quelle
euleriane. Queste ricerche di Lagrange, sono contenute
nella memoria Sur l’intégration de quelques équations
différentielles dont les Indéterminées sont séparées, mais dont chaque membre n’est point intégrable [Misc.
Taurinensia, Tomo IV, 1766–69; Oeuvres, 2, pp.
5–33]. Nel 1778,
con la
memoria Dilucidationes
super methodo elengatissima
qua illustris De La Grange usus est in integranda aequationes differentiali
[Acta Academiae Scientiarum Petropolitanae,
1778, I (1780), pp. 20–57; Opera Omnia,
Serie I, Vol.
21, pp. 1–38], Euler,
alla luce del metodo di Lagrange, ritornò sui suoi risultati
sulle quadrature, in particolare sul teorema di addizione per gli integrali del
tipo 
,
ove P(x) è un polinomio di
quarto grado a radici distinte.
Precisamente egli ottenne che: 
ove z è una funzione algebrica di x e y.
Ma anche questo risultato fu ottenuto in modo
“fortuito” senza seguire un metodo preciso. Euler tentò poi di estendere la formula precedente agli
integrali in cui P(x) ha grado 
, ossia agli integrali che successivamente saranno detti iperellittici.