 General Curves Index General Curves Index
 Curves [A...E] Curves [A...E]
 Curves [F...P] Curves [F...P]
 Curves [P...W] Curves [P...W]
 Astroid Astroid
 Bicorn Bicorn
 Cardioid Cardioid
 Cartesian Oval Cartesian Oval
 Cassinian Ovals Cassinian Ovals
 Catenary Catenary
 Cayley's Sextic Cayley's Sextic
 Circle Circle
 Cissoid of Diocles Cissoid of Diocles
 Cochleoid Cochleoid
 Conchoid Conchoid
 Conchoid of de Sluze Conchoid of de Sluze
 Cycloid Cycloid
 Devil's Curve Devil's Curve
 Double Folium Double Folium
 Dürer's Shell Curves Dürer's Shell Curves
 Eight Curve Eight Curve
 Ellipse Ellipse
 Epicycloid Epicycloid
 Epitrochoid Epitrochoid
 Equiangular Spiral Equiangular Spiral
|
|
| |
Curves Index [A...E]
|
| |
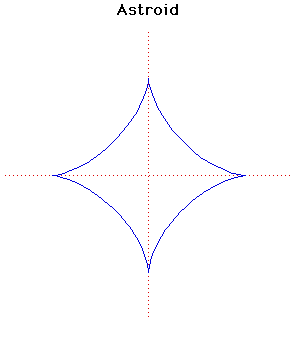
Cartesian equation:
x2/3 + y2/3 = a2/3
or parametrically:
x = a cos3(t), y = a sin3(t)
|
The astroid was first discussed by
Johann Bernoulli in 1691-92.
It also appears in Leibniz's correspondence of 1715.
It is sometimes called the tetracuspid for the obvious reason that it has four cusps.
The astroid only acquired its present name in 1836 in a book published in Vienna.
It has been known by various names in the literature, even after 1836, including cubocycloid and paracycle.
The length of the astroid is 6a and its area is 3
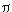 a2/8. a2/8.
The gradient of the tangent T from the point with parameter p is -tan(p).
The equation of this tangent T is
x sin(p) + y cos(p) = a sin(2p)/2
Let T cut the x-axis and the y-axis at X and Y respectively.
Then the length XY is a constant and is equal to a.
It can be formed by rolling a circle of radius a/4 on the inside of a circle of radius a.
It can also be formed as the envelope produced when a line segment is moved with each end on one of a pair
of perpendicular axes. It is therefore a glissette.
|
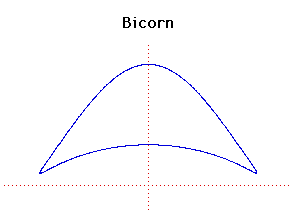 Cartesian equation:
y2(a2 - x2) =
(x2 + 2ay - a)2
Cartesian equation:
y2(a2 - x2) =
(x2 + 2ay - a)2
|
The bicorn (also called the cocked-hat) is the name of a collection of
quartic curves studied by Sylvester
in 1864. The same curves were the studied by
Cayley in 1867.
The particular bicorn given by Sylvester
and Cayley
is a different quartic from the one given here but this one, with a simpler
formula, has essentially the same shape.
|

Cartesian equation:
(x2 + y2 - 2ax)2 = 4a2(x2 + y2)
Polar equation:
r = 2a(1 + cos( )) ))
The cardioid, a name first used by de Castillon in a paper in the
Philosophical Transactions of the Royal Societyin 1741, is a curve that is the locus of a point
on the circumference of circle rolling round the circumference of a circle of equal radius.
Of course the name means 'heart-shaped'.
Its length had been found by La Hire in 1708, and he therefore has some claim
to be the discoverer of the curve. In the notation given above the length is 16a.
It is a special case of the Limacon of Pascal
(Etienne Pascal) and so, in a sense, its study goes back long before
Castillon or
La Hire.
There are exactly three parallel tangents to the cardioid with any given gradient.
Also the tangents at the ends of any chord through the cusp point are at right angles.
The length of any chord through the cusp point is 4a and the area of the cardioid is 6
 a2. a2.
We can easily give parametric equations for the cardioid, namely
x = a(2cos(t) - cos(2t)), y = a(2sin(t) - sin(2t)).
The pedal curve of the cardioid, where the cusp point is the pedal point, is
Cayley's Sextic.
If the cusp of the cardioid is taken as the centre of inversion, the cardioid inverts to a
parabola.
The caustic of a cardioid, where the radiant point is taken to be the cusp, is a
nephroid.
There are some other heart-shaped curves, sent to us by Kurt Eisemann (San Diego State University, USA):
(i) The curve with Cartesian equation: y = 0.75 x2/3

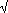 (1 - x2).
Show the picture (1 - x2).
Show the picture
(ii) The curve with Polar equation: r = sin2( /8 - /8 -
 /4).
Show the picture /4).
Show the picture
|
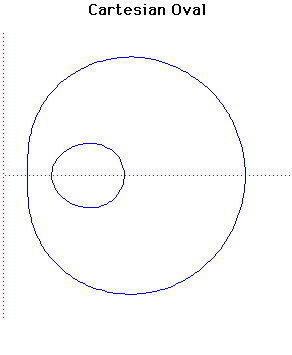
Cartesian equation:
((1 - m2)(x2 + y2) +
2m2cx + a2 -
m2c2)2 =
4a2(x2 + y2)
This curve C consists of two ovals so it should really be called
Cartesian Ovals. It is the locus of a point P whose distances
s and t from two fixed points S and T satisfy
s + mt = a. When c is the distance between S
and T then the curve can be expressed in the form given above.
The curves were first studied by
Descartes
in 1637 and are sometimes called the 'Ovals of
Descartes'.
The curve was also studied by
Newton
in his classification of cubic curves.
The Cartesian Oval has bipolar equation r + mr' =a.
If m =  1 then
the Cartesian Oval C is a central conic while if m =
a/c then the curve is a Limacon of Pascal
(Étienne
Pascal). In this case the inside oval touches the outside one. 1 then
the Cartesian Oval C is a central conic while if m =
a/c then the curve is a Limacon of Pascal
(Étienne
Pascal). In this case the inside oval touches the outside one.
Cartesian Ovals are anallagmatic curves.
|
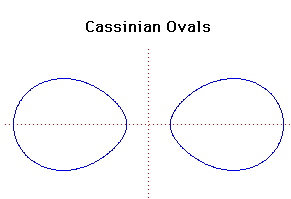
Cartesian equation:
(x2 +
y2)2 - 2a2(x2 -
y2) + a4 - c4 = 0
|
The Cassinian ovals are the locus of a point P that moves so that the
product of its distances from two fixed points S and T [in this
case the points ( a,
0)] is a constant c2. The shape of the curve depends on
c/a. If c > a then the curve consists of two
loops. If c < a then the curve consists of a single loop. The
case where c = a produces a Lemniscate
of Bernoulli (a figure of eight type curve introduced by Jacob
Bernoulli ). a,
0)] is a constant c2. The shape of the curve depends on
c/a. If c > a then the curve consists of two
loops. If c < a then the curve consists of a single loop. The
case where c = a produces a Lemniscate
of Bernoulli (a figure of eight type curve introduced by Jacob
Bernoulli ).
The curve was first investigated by Cassini
in 1680 when he was studying the relative motions of the Earth and the Sun. Cassini
believed that the Sun travelled round the Earth on one of these ovals, with the
Earth at one focus of the oval. Cassini
actually introduced his curves 14 years before Jacob
Bernoulli described his lemniscate.
Cassinian Ovals are anallagmatic curves. They are defined by the bipolar
equation rr' = k2.
Even more incredible curves are produced by the locus of a point the product
of whose distances from 3 or more fixed points is a constant.
|

Cartesian equation:
y = a cosh(x/a)
|
The catenary is the shape of a perfectly flexible chain suspended by its ends
and acted on by gravity. Its equation was obtained by Leibniz,
Huygens
and Johann
Bernoulli in 1691. They were responding to a challenge put out by Jacob
Bernoulli to find the equation of the 'chain-curve'.
Huygens
was the first to use the term catenary in a letter to Leibniz
in 1690 and David
Gregory wrote a treatise on the catenary in 1690. Jungius
(1669) disproved Galileo's
claim that the curve of a chain hanging under gravity would be a parabola.
The catenary is the locus of the focus of a parabola
rolling along a straight line.
The catenary is the evolute of the tractrix.
It is the locus of the mid-point of the vertical line segment between the curves
ex and e-x.
Euler
showed in 1744 that a catenary revolved about its asymptote generates the only
minimal surface of revolution.
|

Cartesian equation:
4(x2 + y2 - ax)3 =
27a2(x2 + y2)2
Polar equation:
r = 4a cos3( /3) /3)
If your browser can handle JAVA code, click HERE to
experiment interactively with this curve and its associated curves.
This was first discovered by Maclaurin
but studied in detail by Cayley.
The name Cayley's
sextic is due to R C Archibald who attempted to classify curves in a paper
published in Strasbourg in 1900.
The evolute of Cayley's Sextic is a nephroid
curve.
|
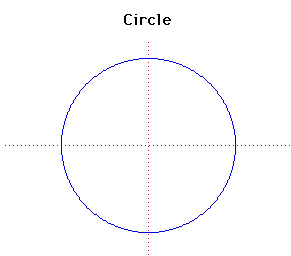
Cartesian equation:
x2 + y2 = a2
or parametrically: x = a cos(t), y = a sin(t)
Polar equation: r = a
The study of the circle goes back beyond recorded history. The invention of
the wheel is a fundamental discovery of properties of a circle.
The greeks considered the Egyptians as the inventors of geometry. The scribe
Ahmes,
the author of the Rhind papyrus, gives a rule for determining the area of a
circle which corresponds to  =
256/81 or approximately 3.16. =
256/81 or approximately 3.16.
The first theorems relating to circles are attributed to Thales
around 650 BC. Book III of Euclid's
Elementsdeals with properties of circles and problems of inscribing and
escribing polygons.
One of the problems of Greek mathematics was the problem of finding a square
with the same area as a given circle. Several of the 'famous curves' in this
stack were first studied in an attempt to solve this problem. Anaxagoras
in 450 BC is the first recored mathematician to study this problem.
The problem of finding the area of a circle led to integration. For the
circle with formula given above the area is  a2 and the length of the curve is
2 a2 and the length of the curve is
2 a. a.
The pedal of a circle is a cardioid
if the pedal point is taken on the circumference and is a limacon
if the pedal point is not on the circumference.
The caustic of a circle with radiant point on the circumference is a cardioid,
while if the rays are parallel then the caustic is a nephroid.
Apollonius,
in about 240 BC, showed effectively that the bipolar equation r =
kr' represents a system of coaxial circles as k varies. In terms
of bipolar equations mr2 + nr'2 =
c2 represents a circle whose centre divides the line segment
between the two fixed points of the system in the ratio n to m.
|
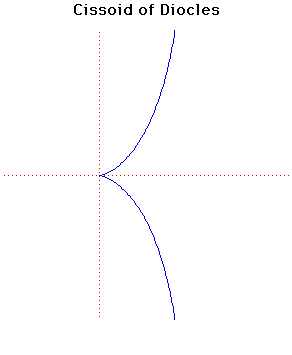
Cartesian equation: y2 =
x3/(2a - x)
Polar equation: r = 2a tan( )sin( )sin( ) )
This curve (meaning 'ivy-shaped') was invented by Diocles
in about 180 BC in connection with his attempt to duplicate the cube by
geometrical methods.
The name first appears in the work of Geminus
about 100 years later. Fermat
and Roberval
constructed the tangent in 1634. Huygens
and Wallis
found, in 1658, that the area between the curve and its asymptote was 3 a2. From a given point there
are either one or three tangents to the cissoid. a2. From a given point there
are either one or three tangents to the cissoid.
The Cissoid of Diocles
is the roulette of the vertex of a parabola
rolling on an equal parabola.
Newton
gave a method of drawing the Cissoid of Diocles
using two line segments of equal length at right angles. If they are moved so
that one line always passes through a fixed point and the end of the other line
segment slides along a straight line then the mid-point of the sliding line
segment traces out a Cissoid of Diocles.
Diocles
was a contemporary of Nicomedes.
He studied the cissoid in his attempt to solve the problem of finding the length
of the side of a cube having volume twice that of a given cube. He also studied
the problem of Archimedes
to cut a sphere by a plane in such a way that the volumes of the segments shall
have a given ratio.
It is in commentaries on Archimedes'
On the sphere and the cylinder that the cissoid appears and is attributed
to Diocles.
The pedal curve of the cissoid, when the pedal point is on the axis beyond
the asymptote, at distance from the cusp four times that of the asymptote, is a
cardioid.
If the cusp of the cissoid is taken as the centre of inversion, the cissoid
inverts to a parabola.
The caustic of the cissoid where the radiant point is taken as (8a, 0)
is a cardioid.
If points P and Q are on the cissoid so that PQ subtends
a right angle at O then the locus of intersection of the tangents at
P and Q lies on the circle with diameter (a/2, 0),
(2a, 0).
|
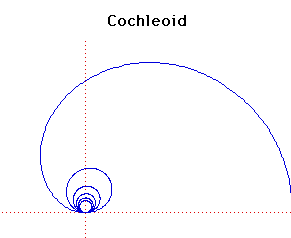
Polar equation: r = a sin( )/ )/
|
The name means the snail-form curve. It was discussed by J Peck in
1700. The form given here is due to a Belgium J. Neuberg.
The name originated in 1884 with writers Benthan and Falkenburg.
The points of contact of parallel tangents to the cochleoid lie on a strophoid.
|
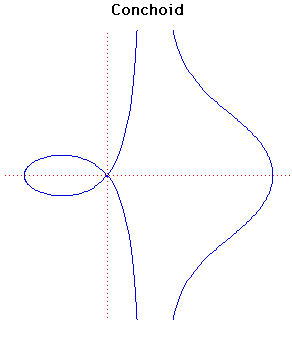
Cartesian equation:
(x - b)2(x2 + y2) - a2x2 = 0
Polar equation: r = a +
b sec( ) )
The name means shell form and was studied by the Greek mathematician
Nicomedes
in about 200 BC in relation to the problem of duplication of the cube.
Nicomedes
recognised the three distinct forms seen in this family.
Nicomedes
was a minor geometer who worked around 180 BC. His main invention was the
conchoid ascribed to him by Pappus.
It was a favourite with 17 Century mathematicians and could be used, as Nicomedes
had intended, to solve the problems of duplicating the cube and trisecting an
angle.
Newton
said it should be a 'standard' curve.
The conchoid has x = b as an asymptote and the area between
either branch and the asymptote is infinite. The area of the loop is
b (a2 - b2) -
2ab log((a + (a2 - b2) -
2ab log((a +  a2 -
b2)/b) +
a2cos-1(b/a). a2 -
b2)/b) +
a2cos-1(b/a).
The conchoid was used in the construction of ancient buildings. The vertical section
of columns was made in the shape of the loop of the conchoid.
|
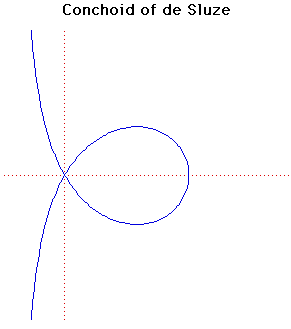
Cartesian equation:
a(x - a)(x2 + y2) =
k2x2
Polar equation:
a(r cos( ) - a) =
k2cos2( ) - a) =
k2cos2( ) )
This curve was first constructed by René de Sluze in 1662.
René Francois Walter- Baron de Sluze
was an important man in the church as well as a mathematician. He contributed to
the geometry of spirals and the finding of geometric means. He also invented a
general method for determining points of inflection of a curve.
|
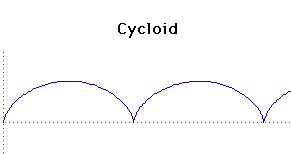
Parametric Cartesian equation:
x =
at - h sin(t), y = a - h cos(t)
The cycloid is the locus of a point at distance h from the
centre of a circle of radius a that rolls along a straight line. If
h < a it is a curtate cycloid while if h >
a it is a prolate cycloid. The curve drawn above has a =
h.
The cycloid was first studied by Cusa
when he was attempting to find the area of a circle by integration.
Mersenne
gave the first proper definition of the cycloid and stated the obvious
properties such as the length of the base equals the circumference of the
rolling circle. Mersenne
attempted to find the area under the curve by integration but failed. He posed
the question to other mathematicians.
The curve was named by Galileo
in 1599. In 1639 he wrote to Torricelli
about the cycloid, saying that he had been studying its properties for 40 years.
Galileo
attempted to find the area by comparing its area to that of the generating
circle. After he failed to find a mathematical method he resorted to weighing
pieces of metal cut into the shape of the cycloid. He found that the ratio of
the weights was approximately 3 to 1 but decided that it was not exactly 3, in
fact he guessed (wrongly) that the ratio was not rational.
Mersenne
proposed the problem of the area to Roberval
in 1628 and, although he failed at first, it was solved by Roberval
in 1634. If a = h then the area under an arch is 3 a2. Roberval,
proud of his result, wrote to Descartes
telling him of it. Descartes
replied that the result was a2. Roberval,
proud of his result, wrote to Descartes
telling him of it. Descartes
replied that the result was
a pretty one which I had not noticed before but which would
cause no difficulty to any moderately skilled geometer. Descartes
challenged Roberval
to find a method of drawing a tangent to the cycloid having discovered himself
how to construct one. Roberval
failed but Fermat,
who was included in the challenge, succeeded.
It is worth noting that Torricelli
independently discovered the area of the cycloid and Viviani
independently found a method for constructing a tangent.
In 1658 Pascal,
after a long spell devoted to religion when he ignored mathematics, started to
think about mathematical problems again as he lay awake at night unable to sleep
for pain. He solved the problem of the area of any segment of the cycloid and
the centre of gravity of any segment. He also solved the problems of the volume
and surface area of the solid of revolution formed by rotating the cycloid about
the x-axis.
Pascal
published a challenge (not under his own name but under the name of Dettonville)
offering two prizes for solutions to these problems. Wallis
and Lalouère entered but Lalouère's solution was wrong and Wallis
was also not successful. Sluze,
Ricci,
Huygens,
Wren
and Fermat
all communicated their discoveries to Pascal
without entering the competition. Wren's
contribution was the most remarkable as he found the arc length, the length of
the arch being 8a.
Pascal
published his own solutions to his challenge problems together with an extension
of Wren's
result which he was able to find.
The cycloid has the property that a particle P sliding on a cycloid
will exhibit simple harmonic motion and the period will be independent of the
starting point. This is the tautochrone property and was discovered by Huygens
in 1673 (Horologium oscillatorium). He constructed the first pendulum
clock with a device to ensure that the pendulum was isochronous by forcing the
pendulum to swing in a cycloid arc. However this presents too many mechanical
problems to make it practical.
Desargues
proposed cycloidal teeth for gear wheels in the 1630's.
In 1696 Johann
Bernoulli, in Acta eruditorum, asked which curve satisfies the
brachistochrone property. He already knew the brachistochrone property of the
cycloid and published his solution in 1697. It was also shown by Leibniz,
Newton,
Jacob
Bernoulli and de
l'Hôpital. It was one of the earliest variational problems and its
investigation was the starting point for the development of the calculus of
variations.
The cycloid is the catacaustic of a circle when the light rays come from a
point on the circumference. This was shown by Jacob
Bernoulli and Johann
Bernoulli in 1692.
The caustic of the cycloid, where the rays are parallel to the y-axis
is a cycloid with twice as many arches.
Both the evolute and involute of a cycloid is an identical cycloid. In fact
the evolute was studied by Huygens
and because of his work on the cycloid Huygens
developed a general theory of evolutes of curves.
|
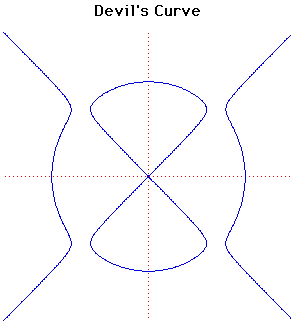
Cartesian equation: y4 -
x4 + a y2 + b
x2 = 0
Polar equation (Special case): r =
 [(25 - 24tan2
( [(25 - 24tan2
( ))/(1 - tan2
( ))/(1 - tan2
( ))] ))]
The Devil's Curve was studied by G. Cramer
in 1750 and Lacroix
in 1810. It appears in Nouvelles Annalesin 1858.
Gabriel Cramer
(1704-1752) was a Swiss mathematician. He became professor of mathematics at
Geneva and wrote on work related to physics; also on geometry and the history of
mathematics. He is best known for his work on determinants (1750) but also made
contributions to the study of algebraic curves (1750).
|
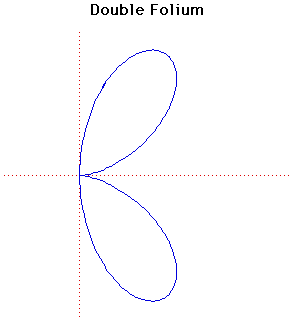
Cartesian equation: (x2 +
y2)2 = 4axy2
Polar equation: r = 4a cos
 sin2 sin2
The general form of the folium is given by the formula
(x2+y2)(y2+x(x+b))
= 4axy2 or, in polar coordinates
r = -b cos + 4a cos + 4a cos sin2 sin2 . . The word folium means
leaf-shaped.
There are three special forms of the folium, the simple folium, the double
folium and the trifolium. These correspond to the cases
b = 4a, b = 0, b = a
respectively in the formula for the general form.
The graph plotted above is the double folium. There are separate entries for
the simple
folium and the trifolium.
The double folium is the pedal curve of the tricuspoid
where the pedal point is mid-point of one of the three curved sides.
|

Cartesian equation: (x2 +
xy + ax - b2)2 =
(b2 - x2)(x - y +
a)2
These curves appear in Dürer's
work Instruction in measurement with compasses and straight edge(1525).
Dürer
calls the curve 'ein muschellini' which means a conchoid, but since it is not a
true conchoid we have called it Dürer's
shell curve (muschellini = conchoid = shell).
This curve arose from Dürer's
work on perspective. He constructed the curve in the following way. He drew
lines QRP and P'QR of length 16 units through Q
(q, 0) and R (0, r) where q + r = 13. The
locus of P and P' as Q and R move on the axes is the
curve. Dürer
only found one of the two branches of the curve.
The envelope of the line P'QRP is a parabola and the curve is
therefore a glissette of a point on a line segment sliding between a parabola
and one of its tangents.
There are a number of interesting special cases:
In the above formula we have:
b = 0 : Curve becomes two coincident straight lines
x2 = 0.
a = 0 : Curve becomes the line pair x = b/ 2, x = -b/ 2, x = -b/ 2 together with the circle x2 +
y2 = b2. 2 together with the circle x2 +
y2 = b2.
a = b/2 : The curve has a cusp at (-2a, a).
|
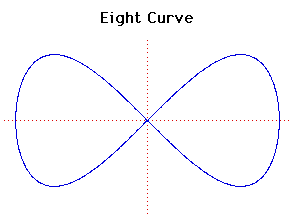
Cartesian equation: x4 =
a2(x2-y2)
Polar equation: r2 =
a2cos(2 )sec4( )sec4( ) )
This curve is also known as the Lemniscate of Gerono.
|
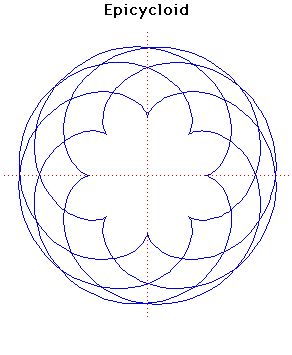
Parametric Cartesian equation: x =
(a + b) cos(t) - b cos((a/b +
1)t), y = (a + b) sin(t) - b
sin((a/b + 1)t)
There are four curves which are closely related. These are the epicycloid,
the epitrochoid,
the hypocycloid
and the hypotrochoid
and they are traced by a point P on a circle of radius b which
rolls round a fixed circle of radius a.
For the epicycloid, an example of which is shown above, the circle of radius
b rolls on the outside of the circle of radius a. The point
P is on the circumference of the circle of radius b. For the
example drawn here a = 8 and b = 5.
These curves were studied by Dürer
(1525), Desargues
(1640), Huygens
(1679), Leibniz,
Newton
(1686), de
L'Hôpital (1690), Jacob
Bernoulli (1690), la
Hire (1694), Johann
Bernoulli (1695), Daniel
Bernoulli (1725), Euler
(1745, 1781).
Special cases are a = b when a cardioid
is obtained and a = 2b when a nephroid
is obtained.
If a = (m - 1)b where m is an integer, then the
length of the epicycloid is 8mb and its area is  b2(m2 +
m). b2(m2 +
m).
The pedal curve, when the pedal point is the centre, is a rhodonea
curve.
The evolute of an epicycloid is a similar epicycloid - look at the evolute of
the epicycloid above to see it is a similar epicycloid but smaller in size.
|
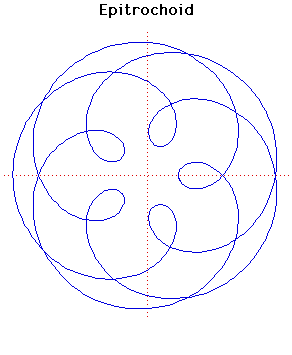
Parametric Cartesian equation: x =
(a + b) cos(t) - c cos((a/b +
1)t), y = (a + b) sin(t) - c
sin((a/b + 1)t)
There are four curves which are closely related. These are the epicycloid,
the epitrochoid, the hypocycloid
and the hypotrochoid
and they are traced by a point P on a circle of radius b which
rolls round a fixed circle of radius a.
For the epitrochoid, an example of which is shown above, the circle of radius
b rolls on the outside of the circle of radius a. The point
P is at distance c from the centre of the circle of radius
b. For the example a = 5, b = 3 and c = 5 (so
P goes inside the circle of radius a).
An example of an epitrochoid appears in Dürer's
work Instruction in measurement with compasses and straight edge(1525).
He called them spider lines because the lines he used to construct the curves
looked like a spider.
These curves were studied by la
Hire, Desargues,
Leibniz,
Newton
and many others.
|

Polar equation: r = a
exp( cot b) cot b)
The equiangular spiral was invented by Descartes
in 1638. Torricelli
worked on it independently and found the length of the curve.
If P is any point on the spiral then the length of the spiral from
P to the origin is finite. In fact, from the point P which is at
distance d from the origin measured along a radius vector, the distance
from P to the pole is d sec b. Jacob
Bernoulli in 1692 called it spira mirabilis and it is carved on his
tomb in Basel.
It occurs naturally in many places like sea-shells where the growth of an
organism is proportional to the size of the organism. In his book Growth and
Form, D'Arcy
Thompson devoted a whole chapter to this curve and describes its occurence
in Nature as the result of coiling a cone upon itself, contrasting it
with the Spiral of
Archimedes which is formed by coiling a cylinder as a sailor coils a rope
upon the deck.
You can see this shell
of the many-chambered Nautilus or the shell with the curve
super-imposed.
The spiral make a constant angle b with any radius vector. Of course
in the special case where b =  /2 one obtains a circle. For the
curve displayed above b = 7 /2 one obtains a circle. For the
curve displayed above b = 7 /16. Therefore the length of the
curve from a point at distance d from the origin along a radius vector is
about 5.126 d. /16. Therefore the length of the
curve from a point at distance d from the origin along a radius vector is
about 5.126 d.
Any radius from the origin meets the spiral at distances which are in
geometric progression.
The pedal of an equiangular spiral, when the pedal point is the pole, is an
identical equiangular spiral.
The evolute and the involute of an equiangular spiral is an identical
equiangular spiral. This was shown by Johann
Bernoulli.
The caustic of the equiangular spiral, where the pole is taken as the
radiant, is an equal equiangular spiral.
|
|
|


