| |
Velocities, Accelerations and Forces
In order to understand the discoveries of Newton, we must have an
understanding of three basic quantities: (1) velocity, (2) acceleration,
and (3) force. In this section we define the first two, and in the next we
shall introduce forces. These three quantities have a common feature: they
are what mathematicians call vectors.
Examples of Scalar Quantities
Vectors are quantities that require not only a magnitude, but a direction to
specify them completely. Let us illustrate by first citing some examples of
quantities that are not vectors. The number of gallons of gasoline in the fuel
tank of your car is an example of a quantitity that can be specified by a
single number---it makes no sense to talk about a "direction" associated with
the amount of gasoline in a tank. Such quantities, which can be specified by
giving a single number (in appropriate units), are called scalars.
Other examples of scalar quantities include the temperature, your weight,
or the population of a country; these are scalars because they are completely
defined by a single number (with appropriate units).
Examples of Vector Quantities
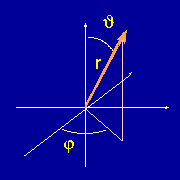 However, consider a velocity. If we say that a car is going 70 km/hour, we
have not completely specified its motion, because we have not specified the
direction that it is going. Thus, velocity is an example of a vector
quantity. A vector generally requires more than one number to specify it; in
this example we could give the magnitude of the velocity (70km/hour), a
compass heading to specify the direction (say 30 degrees from North), and
an number giving the vertical angle with respect to the Earth's surface
(zero degrees except in chase scenes from action movies!).
The adjacent figure shows a typical coordinate system for specifying a vector in terms of
a length r and two angles, theta and phi.
However, consider a velocity. If we say that a car is going 70 km/hour, we
have not completely specified its motion, because we have not specified the
direction that it is going. Thus, velocity is an example of a vector
quantity. A vector generally requires more than one number to specify it; in
this example we could give the magnitude of the velocity (70km/hour), a
compass heading to specify the direction (say 30 degrees from North), and
an number giving the vertical angle with respect to the Earth's surface
(zero degrees except in chase scenes from action movies!).
The adjacent figure shows a typical coordinate system for specifying a vector in terms of
a length r and two angles, theta and phi.
Graphical Representation of Vectors
 Vectors are often distinguished from scalar quantities either by placing a small arrow over the quantity, or by
writing the quantitity in a bold font. It is also common to indicate a vector
by drawing an arrow whose length is proportional to the magnitude of the
vector, and whose direction specifies the orientation of the vector.
Vectors are often distinguished from scalar quantities either by placing a small arrow over the quantity, or by
writing the quantitity in a bold font. It is also common to indicate a vector
by drawing an arrow whose length is proportional to the magnitude of the
vector, and whose direction specifies the orientation of the vector.
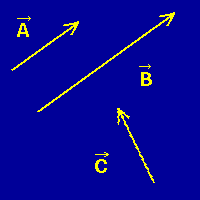
In the adjacent image we show graphical representations for
three vectors. Vectors A and C have the same
magnitude but different directions. Vector B has the same orientation as
vector A, but has a magnitude that is twice as large. Each of these represents
a different vector, because for two vectors to be equivalent they must have
both the same magnitudes and the same orientations.
Velocity and Acceleration
Let us now give a precise definition of velocity and acceleration. They are
vectors, so we must give a magnitude and a direction for them. The
velocity v and the acceleration
a are defined in the following
illustration,

This illustration also demonstrates graphically that velocity (and therefore
acceleration) is a vector: the direction of the rock's velocity is certainly of critical interest to the
person standing under the rock in the two illustrations!
Uniform Circular Motion is Accelerated Motion
 Notice that velocity, which is a vector, is changed if either its magnitude or
its direction is changed. Thus, acceleration occurs when either the magnitude or direction of the velocity (or both) are altered.
Notice that velocity, which is a vector, is changed if either its magnitude or
its direction is changed. Thus, acceleration occurs when either the magnitude or direction of the velocity (or both) are altered.
In particular, notice from the adjacent image that circular motion (even at uniform
angular velocity) implies a continual acceleration, because the direction of the velocity
(indicated by the direction of the arrow) is continuously changing, even if its magnitude (indicated by the length of the
arrow) is constant. This point, that motion on a curved path is accelerated motion, will
prove crucial to our subsequent understanding of motion in gravitational fields.
How Many Accelerators Does Your Car Have?
Be aware that in popular speech acceleration is assumed to be an
increase in the magnitude of the velocity. As we have just seen,
acceleration also occurs when the direction of the velocity is changed, even if
the magnitude is constant; furthermore, in physics a decrease in the
velocity is just as much an acceleration as a decrease.
Thus, your car actually has at least 3 accelerators:
(1) the foot pedal called the "accelerator", that changes the magnitude of the velocity,
(2) the brake, which also changes the magnitude of the velocity, and
(3) the steering wheel, which changes the direction of the velocity!
Newton's Three Laws of Motion
Let us begin our explanation of how Newton changed our understanding of the Universe by enumerating his Three Laws of Motion.
Newton's First Law of Motion:
|
I. Every object in a state of uniform motion tends to remain in that state of motion unless an external force
is applied to it. |
This we recognize as essentially Galileo's
concept of inertia, and this is often termed simply the "Law of Inertia".
Newton's Second Law of Motion:
II. The relationship between an object's mass m, its acceleration a,
and the applied force F is F = m a.
Acceleration and force are vectors; in this law the direction of the force
vector is the same as the direction of the acceleration vector.
|
This is the most powerful of Newton's three Laws, because it allows quantitative
calculations of dynamics: how do velocities change when forces are applied.
Notice the fundamental difference between Newton's 2nd Law and the dynamics of
Aristotle: according to Newton, a force causes only a change in
velocity (an acceleration); it does not maintain the velocity as Aristotle held.
This is sometimes summarized by saying that under Newton, F = ma,
but under Aristotle F = mv, where v is the velocity.
Thus, according to Aristotle there is only a velocity if there is a force, but
according to Newton an object with a certain velocity maintains that
velocity unless a force acts on it to cause an acceleration (that is,
a change in the velocity). As we have noted earlier in conjunction with the discussion of
Galileo,
Aristotle's view seems to be more in accord with common sense, but that is because of a failure to
appreciate the role played by frictional forces. Once account is taken of all forces
acting in a given situation it is the dynamics of Galileo and Newton, not of Aristotle, that are
found to be in accord with the observations.
Newton's Third Law of Motion:
|
III. For every action there is an equal and opposite reaction. |
This law is exemplified by what happens if we step off a boat onto the bank of
a lake: as we move in the direction of the shore, the boat tends to move in
the opposite direction (leaving us facedown in the water, if we aren't careful!).
The Universal Law of Gravitation
There is a popular story that Newton was sitting under an apple tree, an apple
fell on his head, and he suddenly thought of the Universal Law of Gravitation.
As in all such legends, this is almost certainly not true in its details, but the story
contains elements of what actually happened.
What Really Happened with the Apple?
Probably the more correct version of the story is that Newton, upon observing
an apple fall from a tree, began to think along the following lines:
The apple is accelerated, since its velocity changes from zero as it is hanging on the tree and moves toward the ground.
Thus, by Newton's 2nd Law there must be a force that acts on the apple to causethis acceleration.
Let's call this force "gravity", and the associated acceleration the "accleration due to gravity".
Then imagine the apple tree is twice as high.
Again, we expect the apple to be accelerated toward the ground, so this suggests that
this force that we call gravity reaches to the top of the tallest apple tree.
Sir Isaac's Most Excellent Idea
Now came Newton's truly brilliant insight: if the force of gravity reaches to the top of the highest tree, might
it not reach even further; in particular, might it not reach all the way
to the orbit of the Moon! Then, the orbit of the Moon about the Earth could be a consequence of the gravitational
force, because the acceleration due to gravity could change the velocity of the
Moon in just such a way that it followed an orbit around the earth.
This can be illustrated with the thought experiment shown in the
following figure. Suppose we fire a cannon horizontally from a high mountain;
the projectile will eventually fall to earth, as indicated by the shortest
trajectory in the figure, because of the gravitational
force directed toward the center of the Earth and the associated acceleration.
(Remember that an acceleration is a change in velocity and that velocity is a vector, so it has both a magnitude
and a direction. Thus, an acceleration occurs if either or both the magnitude and the direction of the velocity change.)
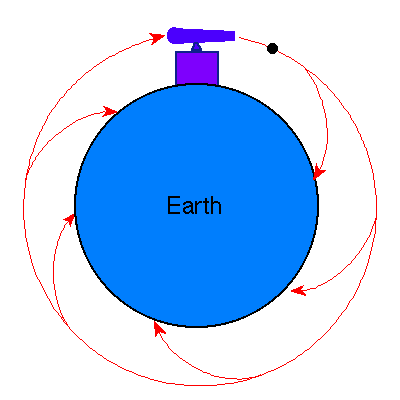
But as we increase the muzzle velocity for our imaginary cannon, the projectile
will travel further and further before returning to earth.
Finally, Newton reasoned that if the cannon projected the cannon ball with
exactly the right velocity, the projectile would travel completely around the
Earth, always falling in the gravitational field but never reaching the Earth,
which is curving away at the same rate that the projectile falls.
That is, the cannon ball would have been put into orbit around the Earth.
Newton concluded that the orbit of the Moon was of exactly the same nature: the Moon continuously "fell" in its path
around the Earth because of the acceleration due to gravity, thus producing its orbit.
By such reasoning, Newton came to the conclusion that any two objects in the
Universe exert gravitational attraction on each other, with the
force having a universal form:

The constant of proportionality G is known as the universal gravitational
constant. It is termed a "universal constant" because it is thought
to be the same at all places and all times, and thus universally
characterizes the intrinsic strength of the gravitational force.
The Center of Mass for a Binary System
If you think about it a moment, it may seem a little strange that in Kepler's
Laws the Sun is fixed at a point in space and the planet revolves around it.
Why is the Sun privileged? Kepler had rather mystical ideas about
the Sun, endowing it with almost god-like qualities that justified its special place.
However Newton, largely as a corollary of his 3rd Law,
demonstrated that the situation actually was more symmetrical than Kepler
imagined and that the Sun does not occupy a privileged postion;
in the process he modified Kepler's 3rd Law.
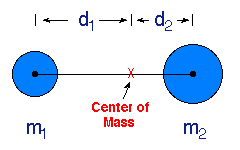 Consider the diagram shown to the right.
We may define a point called the center of
mass between two objects through the equations
Consider the diagram shown to the right.
We may define a point called the center of
mass between two objects through the equations
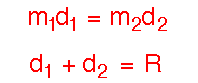
where R is the total separation between the centers of the two objects.
The center of mass is familiar to anyone who has ever played on a see-saw.
The fulcrum point at which the see-saw will exactly balance two people sitting on
either end is the center of mass for the two persons sitting on the see-saw.
Newton's Modification of Kepler's Third Law
Because for every action there is an equal
and opposite reaction, Newton realized that in the planet-Sun system the planet
does not orbit around a stationary Sun. Instead, Newton proposed that both the
planet and the Sun orbited around the common center of mass for the planet-Sun
system. He then modified Kepler's 3rd Law to read,

where P is the planetary orbital period and the other
quantities have the meanings described above, with the Sun as one
mass and the planet as the other mass. (As in the earlier discussion of Kepler's
3rd Law, this form of the equation assumes that masses are measured in solar masses, times in
Earth years, and distances in astronomical units.) Notice the symmetry of this equation:
since the masses are added on the left side and the distances are added on the
right side, it doesn't matter whether the Sun is labeled with 1 and the planet
with 2, or vice-versa. One obtains the same result in either case.
Now notice what happens in Newton's new equation if one of the masses (either 1
or 2; remember the symmetry)
is very large compared with the other. In particular, suppose the Sun is
labeled as mass 1, and its mass
is much larger than the mass for any of the planets.
Then the sum of the two masses is always approximately equal to the mass of the
Sun, and if we take ratios of Kepler's 3rd Law for two different planets the
masses cancel from the ratio and we are left with the
original form of Kepler's 3rd Law:
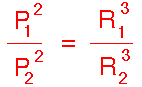
Thus Kepler's 3rd Law is approximately valid because the Sun is much more
massive than any of the planets and therefore
Newton's correction is small. The data Kepler had access to were not good
enough to show this small effect. However,
detailed observations made after Kepler show that Newton's modified form of
Kepler's 3rd Law is in better accord with the data than Kepler's original form.
Two Limiting Cases
We can gain further insight by considering the position of the center of mass
in two limits. First consider the example just addressed, where one mass
is much larger than the other. Then, we see that the center of mass for the
system essentially concides with the center of the massive object:

This is the situation in the Solar System: the Sun is so massive compared with
any of the planets that the center of mass for a Sun-planet pair is always
very near the center of the Sun.
Thus, for all practical purposes the Sun IS almost
(but not quite) motionless at the center of mass for the system, as Kepler
originally thought.
However, now consider the other limiting case where the two masses are equal to
each other.
Then it is easy to see that the center of mass lies equidistant
from the two masses and if they are gravitationally bound to each other,
each mass orbits the common center of mass for the
system lying midway between them:

This situation occurs commonly with
binary stars
(two stars bound gravitationally to each other so that they revolve around their common center
of mass). In many binary star systems the masses of the two stars are similar
and Newton's correction to Kepler's 3rd Law is very large.
Here is a
Java applet that implements Newton's modified form of Kepler's 3rd
law for two objects (planets or stars) revolving around their common center of mass.
By making one mass much larger than the other in this interactive animation you can
illustrate the ideas discussed above and recover Kepler's original form of his 3rd Law
where a less massive object appears to revolve around a massive object fixed at one focus of an ellipse.
These limiting cases for the location of the center of mass
are perhaps familiar from our afore-mentioned playground experience.
If persons of equal weight are on a see-saw, the fulcrum must be
placed in the middle to balance, but if one person weighs much more than the
other person, the fulcrum must be placed close to the heavier person to achieve balance.
Weight and the Gravitational Force
We have seen that in the Universal Law of Gravitation the crucial quantity is
mass. In popular language mass and weight are often used to mean the same
thing; in reality they are related but quite different things. What we
commonly call weight is really just the
gravitational force exerted on an object of a certain mass. We can illustrate by choosing
the Earth as one of the two masses in the previous illustration of the Law of Gravitation:

Thus, the weight of an object of mass m at the surface of the Earth is obtained
by multiplying the mass m by the acceleration due to gravity, g, at the surface
of the Earth. The acceleration due to gravity is approximately the product of
the universal gravitational constant G and the mass of the Earth
M, divided by the radius of the Earth, r, squared.
(We assume the Earth to be spherical and neglect the radius of the object relative to the radius of the
Earth in this discussion.) The measured gravitational acceleration at the
Earth's surface is found to be about 980 cm/second/second.
Mass and Weight
Mass is a measure of how much material is in an object, but
weight is a measure of the gravitational force exerted on that material in a gravitational field;
thus, mass and weight are proportional to each other, with the acceleration due
to gravity as the proportionality constant.
It follows that mass is constant for an object (actually this is not quite true, but we
will save that surprise for our later discussion of the
Relativity Theory),
but weight depends on the location of the object.
For example, if we transported the preceding object of mass m to the surface of
the Moon, the gravitational acceleration would change because the radius and
mass of the Moon both differ from those of the Earth. Thus, our object
has mass mboth on the surface of the Earth and on the surface of the Moon, but it
will weigh much less on the surface of the Moon
because the gravitational acceleration there is a factor of 6
less than at the surface of the Earth.
Newtonian Gravitation and the Laws of Kepler
We now come to the great synthesis of dynamics and astronomy accomplished by
Newton: the Laws of Kepler for planetary motion may be derived from Newton's
Law of Gravitation. Furthermore, Newton's Laws provide corrections to Kepler's
Laws that turn out to be observable, and Newton's Law of Gravitation will be
found to describe the motions of all objects in the heavens, not just the planets.
Acceleration in Keplerian Orbits
 Kepler's Laws are illustrated in the adjacent animation. The red arrow
indicates the instantaneous velocity vector at each point on the orbit
(as always, we greatly exaggerate the eccentricty of the ellipse for purposes
of illustration). Since the velocity is a vector, the direction of the
velocity vector is indicated by the direction of the arrow and the magnitude
of the velocity is indicated by the length of the arrow.
Kepler's Laws are illustrated in the adjacent animation. The red arrow
indicates the instantaneous velocity vector at each point on the orbit
(as always, we greatly exaggerate the eccentricty of the ellipse for purposes
of illustration). Since the velocity is a vector, the direction of the
velocity vector is indicated by the direction of the arrow and the magnitude
of the velocity is indicated by the length of the arrow.
Notice that (because of Kepler's 2nd Law) the velocity vector is constantly changing both its
magnitude and its direction as it moves around the elliptical
orbit (if the orbit were circular, the magnitude of the velocity would remain
constant but the direction would change continuously). Since either a
change in the magnitude or the direction of the velocity vector constitutes an
acceleration, there is a continuous acceleration as the
planet moves about its orbit (whether circular or elliptical),
and therefore by Newton's 2nd Law there is a force that acts at every
point on the orbit. Furthermore, the force is not constant in magnitude, since the change
in velocity (acceleration) is larger when the planet is near the Sun on the elliptical orbit.
Newton's Laws and Kepler's Laws
Since this is a survey course, we shall not cover all the mathematics, but we
now outline how Kepler's Laws are implied by those of Newton, and use Newton's Laws to supply corrections to Kepler's Laws.
- Since the planets move on ellipses (Kepler's 1st Law), they are continually accelerating, as
we have noted above. As we have also noted above, this implies a force acting continuously on the planets.
- Because the planet-Sun line sweeps out equal areas in equal times
(Kepler's 2nd Law), it is possible to show that the force must be directed toward the Sun from the planet.
- From Kepler's 1st Law the orbit is an ellipse with the Sun at one focus;
from Newton's laws it can be shown that this means that the magnitude of the force must vary as
one over the square of the distance between the planet and the Sun.
- Kepler's 3rd Law and Newton's 3rd Law imply that the
force must be proportional to the product of the masses for the planet and the Sun.
Thus, Kepler's laws and Newton's laws taken together imply that the force that
holds the planets in their orbits by continuously changing the planet's
velocity so that it follows an elliptical path is
(1) directed toward the Sun from the planet,
(2) is proportional to the product of masses for the Sun and planet, and
(3) is inversely proportional to the square of the planet-Sun separation. This is precisely the form of the
gravitational force, with the universal gravitational constant G as the constant of proportionality.
Thus, Newton's laws of motion, with a gravitational force used in the 2nd Law, imply
Kepler's Laws, and the planets obey the same laws of motion as objects on the surface of the Earth!
Conic Sections and Gravitational Orbits
The ellipse is not the only possible orbit in a
gravitational field. According to Newton's analysis, the
possible orbits in a gravitational field can take the shape of the figures
that are known as conic sections (so called because they
may be obtained by slicing sections from a cone, as illustrated in the following figure).

For the ellipse (and its special case, the circle),
the plane intersects opposite "edges" of the cone.
For the parabola the plane is parallel to one edge of the cone; for the
hyperbola the plane is not parallel to an edge but it does not
intersect opposite "edges" of the cone.
(Remember that these cones extend forever downward; we have shown them with
bottoms because we are only displaying a portion of the cone.)
Examples of Gravitational Orbits
We see examples of all these possible orbitals in gravitational fields. In
each case, the determining factor influencing the nature of the orbit is the
relative speed of the object in its orbit.
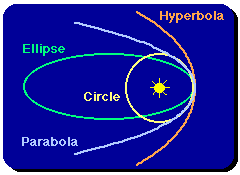
- The orbits of some of the planets (e.g., Venus) are ellipses of such small
eccentricity that they are essentially circles, and we can put artificial
satellites into orbit around the Earth with circular orbits if we choose.
- The orbits of the planets generally are ellipses.
- Some comets have parabolic orbits; this means that they pass the Sun once
and then leave the Solar System, never to return. Other comets have elliptical
orbits and thus orbit the Sun with specific periods.
- The gravitational interaction between two passing stars generally results
in hyperbolic trajectories for the two stars.
Thus, Kepler's elliptical orbitals are but one example of the possible
orbits in a gravitational field. Only ellipses (and their special case, the
circle) lead to bound orbits; the others are associated with one-time
gravitational encounters.
Here is a set of Java applets, taken from the
Famous Curves Applet Index
that illustrate the geometrical properties of these gravitational orbits:
-
Java applet illustrating properties of a circle
-
Java applet illustrating properties of an ellipse
-
Java applet illustrating properties of an hyperbola
-
Java applet illustrating properties of a parabola
For a given central force, increasing the velocity causes the orbit to change
from a circle to an ellipse to a parabola to a hyperbola, with the changes
occurring at certain critical velocities. For example, if the speed of the Earth (which is in a nearly
circular gravitational orbit) were increased by about a factor of 1.4, the orbit would change into a parabola and
the Earth would leave the Solar System.
Gravitational Perturbations and the Prediction of New Planets
Computing the orbit of the Earth as an ellipse around the center of mass for
the Earth-Sun system assumes that they are the only two masses in the Universe.
In reality, the Universal Law of Gravitation implies that the Earth interacts
gravitationally not only with the Sun, but with every other mass in the
Universe: the Moon, the other planets, asteroids and comets, the distant stars.
The Two-Body Approximation
However, from the form of the
gravitational force

we see that the interactions are largest when two situations are fulfilled:
(1) the product of the masses of the two objects is large, which maximizes the
numerator of the expression for the strength of the gravitational force, and
(2) the objects are near each other, which minimizes the denominator of the force equation.
The two-body approximation
that the orbits of the planets are determined only by the
gravitational interaction between the Sun and the planet is possible because
- The Sun is so massive compared with every other object in the Solar System,
- Objects outside the Solar System such as stars are so distant that the
distance squared factor in the denominator renders their gravitational
interactions with the planets negligible.
For example, the Sun is about 300,000 times more massive than the Earth, and
about 1000 times more massive than the largest planet. Thus, the
product of the mass of a planet and the mass of the Sun is always much larger
than the product of the masses of any two planets, and it is a good initial
approximation to neglect all interactions except that of the planet and the
Sun.
Gravitational Perturbations
However, the small deviations from this ideal picture have consequences
if careful measurements are made. These small deviations from the simplified picture are called
perturbations. They can be calculated systematically using Newton's
laws of motion and gravitation from the positions of the known masses in the Solar System.
If we account carefully for all known gravitational
perturbations on the motion of observed planets and the motion of the planet
still deviates from the prediction, there are two options:
- Newton's Law of Gravitation requires modification,
- There is a previously undetected mass that is perturbing the orbits of the
observed planets.
We shall see that the history of astronomy following the introduction of the
Law of Gravitation by Newton gives examples of both.
The Discovery of the New Planet Neptune
 In 1846, the planet Neptune was discovered after its existence was predicted because of
discrepancies between calculations and data for the planet Uranus.
Astronomers found the new planet almost exactly at the position predicted by the
calculations of Leverrier (Adams had also calculated the position
independently). We illustrate the situation schematically in the adjacent
diagram. The dominant interaction between Uranus and the Sun is indicated with
the heavy line, but some perturbations associated with other masses are
indicated by thin lines. By using Newton's laws to calculate the perturbations
on the orbit of Uranus by an hypothesized new planet, Leverrier and Adams were
able to predict where the planet had to be in order to cause the observed
deviations in the position of Uranus.
Once astronomers took this calculation seriously, they found the new
planet within hours of turning their telescopes on the region of the
sky implicated by the calculations.
In 1846, the planet Neptune was discovered after its existence was predicted because of
discrepancies between calculations and data for the planet Uranus.
Astronomers found the new planet almost exactly at the position predicted by the
calculations of Leverrier (Adams had also calculated the position
independently). We illustrate the situation schematically in the adjacent
diagram. The dominant interaction between Uranus and the Sun is indicated with
the heavy line, but some perturbations associated with other masses are
indicated by thin lines. By using Newton's laws to calculate the perturbations
on the orbit of Uranus by an hypothesized new planet, Leverrier and Adams were
able to predict where the planet had to be in order to cause the observed
deviations in the position of Uranus.
Once astronomers took this calculation seriously, they found the new
planet within hours of turning their telescopes on the region of the
sky implicated by the calculations.
This precise prediction of the new planet and its
location was striking confirmation of the power of Newton's theory of
gravitation. (Although in truth it must be said that both Leverrier and Adams
made an incorrect assumption in their calculations concerning the radius of the
new planet's orbit. Fortunately, the error largely cancelled out of the
calculations and had little effect on their final results.)
The Accidental Discovery of Pluto
Later, similar calculations on supposed perturbations of the orbits of Uranus
and Neptune suggested the presence of yet another planet beyond the orbit of
Neptune. Eventually, in 1930, a new planet Pluto was discovered, but we now
know that the calculations in this case were also in error because of an
incorrect assumption about the mass of the new planet. It is now believed that
the supposed deviations in the orbits of Neptune and Uranus were errors in
measurement because the actual properties of Pluto would not have accounted for
the supposed perturbations. Thus, the
discovery of Pluto
was a kind of accident.
Effects Beyond Newtonian Perturbations
The power of Newton's theory became apparent as detailed
calculations accounted more and more precisely for the orbits of the planets.
Any deviations from the expected behavior soon became viewed as evidence for
unseen masses in the Solar System. However, later
observations of anomalies in the orbit of Mercury could not be accounted for by
the gravitational perturbation of a new planet
(the hypothetical new planet, which turned out not to exist, was called
Vulcan).
Early in this century this forced the replacement of
Newton's Law of Gravitation with Einstein's Theory of
General Relativity.
|


