| |
Albert Einstein demoli' completamente la fisica newtoniana, dimostrando l'identita' di ogni legge dedotta
sperimentalmente da due osservatori in diversi sistemi di riferimento (uno sulla Terra l'altro su un razzo) rendendo
privo di senso qualsiasi sistema assoluto.
Einstein getto' le basi della meccanica quantistica anche se non la accetto' mai completamente in quanto non concepiva un universo
regolato da leggi probabilistiche.
I due postulati della teoria della Relativita'
Il primo postulato dice che nessun esperimento compiuto all'interno di un ambiente puo' consentire di determinare lo stato
di quite o di moto rettilineo uniforme dell'ambiente stesso in cui l'esperimento viene compiuto.
Il secondo postulato, dice che la velocita' della luce (o piu' in generale della radiazione elettromagnetica) nel vuoto,
e' costante, da qualunque sorgente venga emessa e da qualunque osservatore venga misurata, ed e' la massima velocita'
consentita in natura.
Sistemi di riferimento inerziali
Consideriamo due sistemi di riferimento inerziali
(sistemi in cui vale la prima legge di Newton) S ed S'
con S' che si muove con velocità costante v rispetto ad
S e per comodità ipotizziamo, senza perdere di generalità, che gli
assi x e x' siano coincidenti e che il vettore velocità sia
parallelo ad essi.
Supponiamo ora che si verifichi un evento fisico in un punto P e
di voler rilevare le sue coordinate spazio-temporali.
Per un osservatore solidale con S avremo coordinate x,
y, z e t (le prime tre sono quelle spaziali) mentre per
quello solidale con il sistema S' lo stesso evento avrà coordinate
x', y', z', t'.
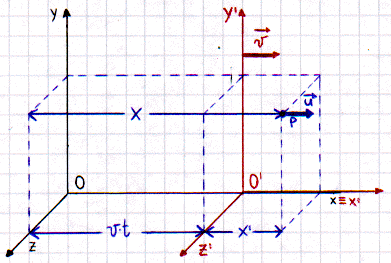
Vediamo ora quali relazioni sussistono fra le due differenti
misurazioni. Dalla figura risultano evidenti le seguenti uguaglianze
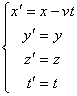
Quest'ultime prendono il nome di Trasformazioni delle coordinate
di Galileo.
Con semplici calcoli si dimostra che
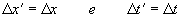
Vediamo ora quali relazioni sussistono per la velocità u
di un oggetto rispetto i due riferimenti. Deriviamo pertanto lo spazio
rispetto al tempo
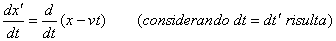
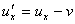
Similmente
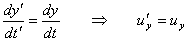
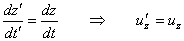
In notazione vettoriale risulta u' = u - v .
Bisogna in ultimo ricordare che, nell'ambito di questa
teoria, anche l'accelerazione e la massa di un corpo, come il tempo, sono
indipendenti dal moto relativo di sistemi di riferimento inerziali e
dunque è vera la seguente uguaglianza ma = m'a' ==>
F=F'.
Con ciò possiamo affermare che le leggi del moto di
Newton e le equazioni del moto di una particella sono le stesse in tutti i
sistemi di riferimento inerziali.
Da questa considerazione finale nasce il
principio di relatività galileiana.
Esso afferma che se due sistemi di riferimento inerziali
sono in moto uno rispetto all'altro è impossibile, dall'interno di uno dei
due riferimenti, stabilire qual'è in movimento: il moto assoluto
non può essere rilevato.
Trasformazioni di Lorentz
Le trasformazioni delle coordinate di Lorentz per
due sistemi di riferimento inerziali S e S', con S'
che si muove con velocità costante v rispetto a S, e del
vettore velocità u di un corpo parallelo agli assi coincidenti x
e x' sono
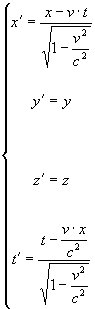

Cerchiamo ora di ricavare, con l'ausilio delle derivate e
dei due postulati fondamentali della relatività, queste trasformazioni.
Basandoci sull'ipotesi che lo spazio ed
il tempo siano omogenei (tutti i punti nello spazio e nel tempo sono
equivalenti) ci aspettiamo che le equazioni di trasformazione cercate
siano lineari, cioè equazioni di primo grado
(1) 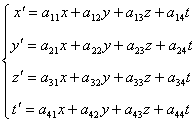
Vediamo ora come determinare i sedici coefficienti aij.
Per le ipotesi fatte sui sistemi di
riferimento S ed S', risulta che gli assi x ed x'
sono sempre fra loro coincidenti e quindi quando y=0, z=0
(coordinate dei punti dell'asse x) deve risultare sempre
y'=0, z'=0 (coordinate dei punti dell'asse x'). Per
sostituzione nella (1) risulta
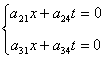
Poiché queste equazioni devono essere verificate per ogni
x e t è evidente che i coefficienti: a21, a24, a31, a34 devono essere zero
sempre. Quindi le formule di trasformazione per y e z
devono essere del tipo
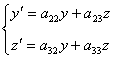
Applichiamo lo stesso ragionamento ai piani x-y
(caratterizzato da z=0) e x-z (caratterizzato da
y=0) che risultano essere sempre coincidenti rispettivamente
ai piani x'-y' (z'=0) e x'-z'(y'=0)
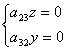
Anche questa volta i coefficienti a23 e a32 devono
essere sempre uguali a zero. Le trasformazioni cercate per y
e z dovranno allora avere la seguente forma
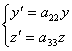
Determiniamo ora tali costanti utilizzando il principio di
relatività.
Ipotizziamo di posizionare un'asta di lunghezza unitaria,
rispetto un osservatore solidale con S, lungo l'asse y.
Secondo un osservatore posto in S' l'asta avrà lunghezza a22 (cioè y'=a22* 1). Se
adesso ipotizziamo di posizionare la stessa asta lungo l'asse y',
l'osservatore del riferimento S misura per la sbarra una lunghezza
pari a 1/a22.
Per il primo postulato della relatività tali grandezze
devono risultare identiche
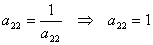
Con lo stesso procedimento troviamo che a33=1. Le prime
due equazioni cercate sono

Rimangono ora le equazioni di
trasformazione per x' e t'.
Consideriamo dapprima l'equazione per t'.
Basandoci sulla ipotesi della isotropia dello spazio
dobbiamo necessariamente supporre che t' non dipenda ne da
y' e ne da z'. Quindi a42 e a43 devono essere necessariamente
uguali a zero.
Per quanto riguarda invece l'equazione per x',
sappiamo che un punto di coordinata x'=0 per S' sembra
muoversi nel verso positivo dell'asse x con velocità v,
quindi l'affermazione x'=0 deve essere identica a quella
x=vt

Combinando le due otteniamo
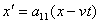
Le nostre quattro equazioni si sono ora ridotte alle
(2)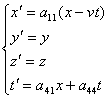
Per determinare i coefficienti a11, a41, a44 utilizziamo il principio della
costanza della velocità della luce.
Ipotizziamo che al tempo t=t'=0 un'onda
elettromagnetica sferica lasci le origini coincidenti dei riferimenti. Per
il postulato suddetto, l'onda si propagherà con velocità c in tutte
le direzioni. Tale propagazione è descritta dalle equazioni di due sfere
uguali di raggio variabile ct e ct'
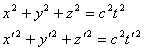
Se ora sostituiamo nella seconda equazione le trasformazioni
della (2) otteniamo
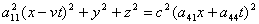
Sviluppando e raccogliendo a fattore comune abbiamo

Affinché questa espressione rappresenti l'equazione della
prima sfera deve risultare
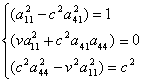
Risolvendo il sistema avremo
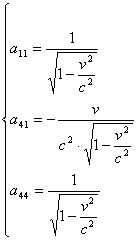
ed infine, sostituendo questi valori per i tre coefficienti
a11,
a41,
a44 nel
sistema (2), otteniamo le trasformazioni di Lorentz per le
coordinate spazio temporali
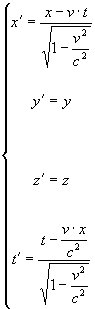
La radice 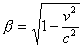 prende il nome di fattore
relativistico. prende il nome di fattore
relativistico.
Derivando infine le funzioni
x'(x,t), y'(x,t), z'(x,t) e t'(x,t) ricaviamo
invece le componenti del vettore u.
Per ux risulta
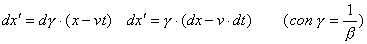
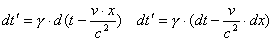
Facendo il rapporto fra i due differenziali abbiamo
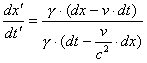
ora semplifichiamo e dividiamo numeratore e denominatore per dt
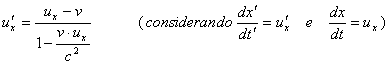
Nello stesso modo possiamo determinare le altre due
componenti del vettore u.

Risulta evidente che quando la velocità
v è trascurabile rispetto a c il fattore relativistico tende
a 1 restituendoci così le trasformazioni di Galileo di cui abbiamo
già parlato.
La teoria della Relativita' Speciale
Nel 1906, Einstein, enuncia la Teoria della relativita' speciale secondo la quale spazio e tempo sono strettamente
interconnessi e formano un continuo dinamico quadridimensionale.
La massa non e' altro che una forma di energia, e vale :
E = m c^2
Velocita' limite
Analizzando le leggi della fisica classica si nota
che esse non impongono nessuna limitazione all'intensità del vettore velocità di un corpo.
Possiamo così ipotizzare, ad esempio, l'esistenza di un'onda che viaggi
a velocità v infinita.
Tale onda sarebbe quindi in grado di attraversare tutte le parti del
nostro universo in un tempo nullo. Risulta evidente (e quasi logico) che
tale realtà non è attualmente realistica ed inoltre nessun esperimento ha mai confermato tale ipotesi.
Nelle equazioni di Lorentz è presente il fattore relativistico
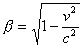
Esso impone che il vettore velocità v abbia una
intensità non maggiore di c poiché se così fosse b rappresenterebbe la radice di un numero
negativo e questa cosa non è algebricamente accettabile poiché non si
definiscono, come l'algebra insegna, radici di numeri negativi.
La velocità limite per il moto di qualunque oggetto naturale
è dunque c.
Attenzione però, c è una velocità limite solo per gli
oggetti naturali. I fenomeni cinematici possono avere una velocità
maggiore di quella delle onde elettromagnetiche. Ad esempio se
consideriamo un palio di forbici giganti, dobbiamo sicuramente muovere le
sue lame con una velocità inferiore a c ma la successione dei punti
di intersezione delle lame può avere una velocità maggiore di quella limite!
Contrazione lunghezze
Un'altra conseguenza, che cozza con il nostro senso
comune, è questa: la lunghezza di un corpo è più grande quando questo è
a risposo relativamente all'osservatore. Quando il corpo si muove con una
velocità v rispetto all'osservatore la sua lunghezza si
contrae, nella direzione del moto, del fattore b.
Vediamo di dimostrare quanto affermato.
Consideriamo i nostri due soliti sistemi di
riferimento inerziali S ed S' e posizioniamo un'asta ferma
lungo l'asse x' del riferimento accentato. Per un osservatore
solidale con il sistema in moto, le coordinate degli estremi dell'asta
saranno x'1 e x'2. La sua lunghezza è

Per l'osservatore in S, invece, l'asta si muove con
velocità relativa v e quindi, per le trasformazioni di Lorentz, abbiamo
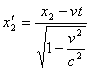
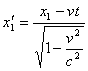
facciamo la differenza membro a membro ed otteniamo
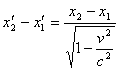
La lunghezza dell'asta, per l'osservatore nel sistema
S, è allora diminuita del fattore relativistico. Risulta
infatti
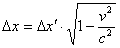
Abbiamo così dimostrato quanto in precedenza affermato.
Dilatazione tempi
La conseguenza però più strabiliante, è questa: un orologio va al ritmo più veloce quando è a riposo rispetto
all'osservatore. Quando si muove con velocità v rispetto
all'osservatore, il suo ritmo misurato subisce un rallentamento di un
fattore b.
Per la dimostrazione consideriamo ancora una volta i sistemi di
riferimento S ed S' ed un orologio situato in una posizione
fissa x' nel riferimento S'.
Ipotizziamo ora che avvenga un evento fisico nel
sistema S' e di misurare la durata dello stesso. L'orologio
considerato misura i tempi t'1 e
t'2 indicanti rispettivamente
l'inizio e la fine dell'evento.
L'osservatore in S, invece, misura con lo stesso orologio due
tempi t1 e t2.
Per quest'ultimo osservatore però l'orologio ha mutato la sua posizione
poiché si è mosso con velocità costante v e di conseguenza
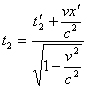
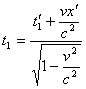
facciamo la differenza membro a membro ed otteniamo
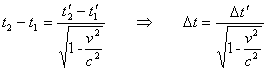
Per l'osservatore solidale con S' il tempo si è
dilatato!
Massa relativa
Vediamo ora, senza dimostrazione, che anche la massa
di un corpo varia quando esso si muove con velocità costante v.
Intuitivamente possiamo iniziare la nostra analisi
considerando le leggi classiche della dinamica in base alle quali
(1) 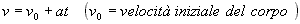
Risulta però evidente che scelta una accelerazione a
possiamo far trascorrere un tempo tanto lungo da rendere v maggiore
di c e questa ipotesi non è accettabile poiché, come già visto,
nessun corpo può viaggiare più veloce della luce.
In base al secondo principio di Newton sappiamo che
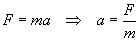
di conseguenza, con una semplice sostituzione, la (1) diventa

A questo punto, se ipotizziamo essere F costante, è
l'aumento della massa m che permette al vettore v di non
avere una intensità maggiore di c.
L'equazione che esprime la variazione della massa di un
corpo è la seguente
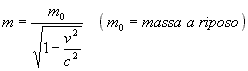
Energia relativa
Analizziamo ora una delle equazioni più famose e
ricordate della fisica moderna
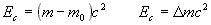
Questa, che prende il nome di Equazione relativistica per
l'energia, rappresenta una nuova legge per l'energia cinetica di una
particella che si muove con velocità v.
Sviluppando l'equazione otteniamo
(1)
L'espressione risulta così costituita da due termini. Il
primo dipende dalla velocità v del corpo mentre il secondo è
indipendente da essa e pertanto prende il nome di energia di riposo o
di quiete.
Questa legge sembra discostarsi molto
dalla classica equazione per l'energia cinetica ma in realtà, quando
v è molto minore di c, le due equazioni si assomigliano.
Usando la formula di Mac-Laurin (considerando come variabile del polinomio
v/c e fermandoci alla derivata seconda) otteniamo la seguente
approssimazione per 1/b
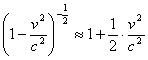
Con una semplice sostituzione nella (1) otteniamo l'equazione classica per l'energia
cinetica
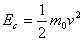
L'identificazione del termine

come energia di riposo non è solo una convenzione.
Gli studi e gli esperimenti odierni hanno mostrato che la conversione
dell'energia di riposo in energia cinetica, con una corrispondente perdita
di massa, è un fenomeno che si verifica comunemente e continuamente nel
decadimento radioattivo e nelle reazioni nucleari.
Tale scoperta determinò l'inizio del
periodo nucleare e furono proprio gli studi svolti dallo scienziato Albert
Einstein, in America, che permisero la realizzazione delle prime bombe
nucleari che furono utilizzate dagli stessi americani per determinare le
sorti del secondo conflitto mondiale.
La teoria della Relativita' Generale
La teoria della relatività ristretta permette la
descrizione dei fenomeni meccanici ed elettromagnetici mediante leggi
valide qualunque siano gli osservatori solo se essi sono dotati di moto
rettilineo uniforme.
Per eliminare questa limitazione, nel 1915, Einstein
generalizzò la sua teoria in modo da renderla utilizzabile
indipendentemente dal moto dell'osservatore. Il punto di partenza dello
scienziato fu il campo gravitazionale.
Consideriamo una zona di spazio priva di forze gravitazionali ed in
essa una astronave con un osservatore.

Se la navicella inizia a muoversi verso l’alto con moto uniformemente
accelerato e l’osservatore lascia una sfera, questa risentirà
dell'accelerazione e dopo che il pavimento l'avrà raggiunta eserciterà
sullo stesso una forza pari al prodotto della sua massa per
l'accelerazione del sistema.
L’osservatore vedrà invece cadere la sfera sul pavimento e giungerà
alla conclusione di trovarsi in una zona soggetta ad un campo
gravitazionale costante nel tempo.
Si può allora affermare che il campo gravitazionale apparente, prodotto
da un semplicissimo moto accelerato, non è distinguibile da un vero campo
dovuto all’attrazione di una massa.
In questa conclusione risiede il principio d’equivalenza tra gravità e
accelerazione:
Un campo gravitazionale omogeneo è del tutto equivalente ad
un sistema di riferimento uniformemente
accelerato.
La teoria generale della relatività deriva direttamente dal principio
di equivalenza e permette di ricavare teoricamente le proprietà del campo
gravitazionale, la sua influenza sui fenomeni naturali e di formulare le
leggi cui obbedisce il campo gravitazionale stesso.
Il procedimento che porta però alla formulazione di tali leggi impone
di abbandonare la concezione comune dello spazio a tre dimensioni; esso
diviene, infatti, uno spazio curvo per la cui rappresentazione viene
impiegato un diverso sistema di coordinate dette Gaussiane.
In questo modo il principio di relatività diviene:
Tutti i sistemi di coordinate sono equivalenti per
principio per formulare le leggi generali della
natura.
Einstein giunse grazie alla relatività generale a formulare le leggi
sul campo gravitazionale che oggi noi conosciamo.
Esse soddisfano i postulati formulati dallo stesso Einstein, non
violano il principio di conservazione dell’energia e della quantità di
moto e inglobano le stesse leggi newtoniane sulla gravitazione.
Attualmente grazie alla soluzione "dell'equazione di campo"
einsteiniana è possibile stabilire, nota la distribuzione di massa, la
curvatura spazio-tempo in una determinata regione dell'universo, prevedere
la deflessione della luce in prossimità di grandi masse, il moto del
perielio delle orbite planetarie e lo spostamento verso il rosso della
luce prodotta da sorgenti luminose gravitazionali.
La dimostrazione delle leggi formulate solo teoricamente da Einstein
avvenne intorno al 1960 con l’avvento di strumenti più sofisticati e per
questo, mentre la teoria della relatività ristretta costituì subito uno
dei pilastri della fisica moderna, fu solo con le grandi scoperte
dell’astrofisica che la relatività generale acquistò quel ruolo preminente
che oggi le compete.
Consequenze della Teoria della Relativita' Generale
- Tempo, spazio e massa diventano quantita' interdipendenti
- La massa di un corpo aumenta fino a diventare infinita alla velocita' della luce
- Il tempo si dilata fino a fermarsi alla velocita' della luce
- La lunghezza di un oggetto si riduce fino a zero alla velocita' della luce
- Lo spazio viene incurvato dalle masse gravitazionali
Supponiamo adesso una navicella lunga 100 metri con una massa di 100 tonnellate che accellera la sua velocita' dallo
stato di quite fino alla velocita' della luce, avremmo i seguenti valori:
| Velocita' della luce | Lunghezza | Massa | Durata del tempo |
| (%) | (metri) | (tonnellate) | (Terra=60 min) |
| 0 | 100 | 100 | 60 |
| 10 | 99.5 | 100.5 | 59.52 |
| 30 | 95.395 | 104.83 | 57.2 |
| 50 | 86.6 | 115.47 | 52.1 |
| 80 | 60 | 166.67 | 36 |
| 90 | 43.59 | 229.42 | 26.18 |
| 99 | 14.11 | 708.88 | 8.53 |
| 99.9 | 4.47 | 2236.63 | 2.78 |
| 99.997 | 0.071 | 14142.2 | 1.17 |
| 100 | zero | infinito | zero |
La tabella indica che nessuna navicella puo' viaggiare alla velocita' della luce, in quanto avrebbe una massa infinita,
e questo comporterebbe un motore di infinita potenza. Anche se comunque, questo motore fosse realizzato, la navicella
avrebbe lunghezza pari a zero, cioe' non esisterebbe! Questo agli occhi un osservatore esterno. Un viaggiatore all'interno
della navicella invece non riscontrerebbe nulla di anormale.
Gli effetti piu' drastici della curvatura dello spazio e del tempo si manifestano durante la contrazione o collasso
gravitazionale di una stella di grande massa.
Nel corso della sua evoluzione ogni stella raggiunge uno stadio durante il quale essa si contrae a causa della mutua
attrazione gravitazionale tra le sue particelle.
Poiche' l'attrazione aumenta rapidamente col diminuire della distanza tra le particelle, la contrazione accellera e
prosegue indefinitivamente. La stella diventa sempre piu' densa, la forza di gravita' sulla sua superficie cresce
sempre di piu', e di conseguenza continua ad aumentare anche la curvatura dello spazio-tempo nella regione circostante.
A causa della crescente forza di gravita', diventa sempre piu' difficile allontanarsi dalla superficie, fino al punto
limite
in cui nulla puo' sfuggire dalla stella, neppure la luce. Non siamo piu' in grado di vedere la stella anche se siamo in
presenza di un corpo di grandissima densita' chiamato buco nero.
Il fenomeno ha effetti altrettanto impressionanti sul tempo, supponiamo infatti che un orologio ci inviasse i suoi segnali
dalla superficie di una stella che si sta contraendo. I segnali rallenterebbero sempre di piu' fino a fermarsi completamente,
la contrazione della stella avverrebbe quindi in un tempo infinito. Tuttavia sulla superficie della stella, non si
avvertirebbe nulla di particolare, il tempo continuerebbe a scorrere normalmente e la contrazione sarebbe completata
dopo un periodo finito di tempo, quando la stella si e' contratta in un punto di densita' infinita.
Allora, quanto tempo occorre realmente per la contrazione, finito o infinito ?
Nel mondo della teoria della Relativita' una domanda di questo genere e' priva di senso. La durata della vita di una
stella che si contrae, come tutti gli intervalli di tempo, e' relativa e dipende dal sistema di riferimento
dell'osservatore.
L'equazione di Dio
Senza dubbio il dibattito fra gli scienziati continuerà finché proseguiranno i loro tentativi di svelare il mistero dell'universo, ma c'è una cosa sulla quale tutti concordano: la potenza e la perenne utilità della teoria einsteiniana della relatività generale. In ultima analisi, una conoscenza più completa dei "pensieri di Dio" ci imporrebbe di incorporare delle considerazioni quantistiche nella teoria della relatività, ma quale che sia la formula finale, l'equazione del campo di Einstein ne sarà magna pars. Creando questa straordinaria equazione Einstein realizzò il sogno di tutta la sua vita: ascoltare almeno una parte dei pensieri di Dio, In effetti, la migliore approssimazione che abbiamo all'equazione di Dio è la formula einsteiniana del campo con costante cosmologica,
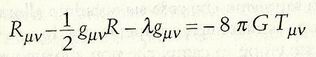
dove Ruv è il tensore di Ricci, R la sua traccia, Lamda la costante cosmologica, guv la misura della distanza (cioè il tensore metrico della geometria dello spazio), G la costante gravitazionale di Newton e Tuv il tensore che esprime le proprietà di energia, impulso e materia, mentre 1/2, 8 e Pi non sono che numeri.
Nel suo Pensieri degli anni difficili Einstein accenna brevemente alla sua visione del futuro e alle ragioni per cui non era riuscito a creare una teoria unificata di tutte le cose:
La teoria generale della relatività è ancora incompleta nel senso che è stata capace di applicare in modo soddisfacente il principio di relatività solo ai campi gravitazionali, ma non al campo totale. Non sappiamo ancora con certezza né quale sia il meccanismo matematico con cui descrivere il campo totale nello spazio né a quali leggi invarianti e generali questo campo totale sia soggetto. Ma una cosa appare certa: il principio generale di relatività sarà uno strumento indispensabile ed efficace della soluzione di questo problema del campo totale.
Einstein si rendeva conto che i suoi sforzi erano stati bloccati dalle limitazioni dei metodi matematici esistenti. Per creare la relatività speciale aveva usato la matematica dì Lorentz e Minkowski, dopo di che, per la relatività generale aveva usato quella di Ricci e Levi Civita nonché quella di Riemann, e qui aveva dovuto fermarsi. Aveva fatto molta strada verso l'equazione di Dio, ma per andare ancora più avanti avrebbe avuto bisogno di un tipo nuovo di matematica, che comprenderà una geometria e una topologia portate a un livello di astrazione più alto.
I matematici creeranno gli strumenti, i fisici li applicheranno, gli astronomi verificheranno le teorie e forniranno i dati e i cosmologi produrranno la grande visione d'insieme del nostro universo. Così, una volta che ogni singola disciplina troverà un punto d'appoggio in qualche nuovo sviluppo delle altre, potremo forse cominciare a capire le leggi ultime della natura e a formulare la nostra umana interpretazione dell'equazione di Dio; quando l'equazione definitiva sarà stata costruita, dovremmo essere in grado di usarla per risolvere lo splendido enigma della creazione.
E forse è proprio per questo che Dio ci ha messi dove ci ha messi.
(Tratto da "L'equazione di Dio" di Amir D. Aczel - 2000 Il Saggiatore)
|


