Capitolo 8

Le equazioni differenziali rappresentano uno strumento di base nella modellistica matematica in svariati campi applicativi, dalla meccanica, all'astronomia, alle scienze economiche e più recentemente alla chimica, alla biologia, all'informatica

Tuttavia, affinché il modello matematico che ne deriva sia utile, occorrono validi strumenti risolutivi. Tali strumenti possono essere di natura qualitativa, quando danno informazioni sul comportamento della soluzione, o di tipo quantitativo quando forniscono approssimazioni numeriche delle soluzioni.

Spesso nelle applicazioni i due aspetti sono ugualmente importanti e in ogni caso possono integrarsi tra loro utilmente. Infatti, uno studio preliminare dell'equazione può suggerire il metodo numerico più adatto e viceversa uno studio sperimentale mediante metodi numerici può fornire indicazioni su aspetti qualitativi della soluzione.

Un generico problema di equazioni differenziali ordinarie, si può ricondurre allo studio di un insieme di n equazioni differenziali di primo ordine, aventi forma generale:

dove le funzioni f_i sono note. I problemi concernenti le ODE non sono completamente specificati dalle loro equazioni. E' importante, per poter risolverle, conoscere le condizioni al contorno. Generalmente, il metodo numerico applicabile sarà deciso proprio in funzione delle condizioni al contorno. I problemi a valori al contorno si dividono in due categorie molto più ampie. Problemi a valori iniziali, in cui sono noti i valori che assumono le y_i in corrispondenza di alcuni punti iniziali x_s. Problemi a valori in due punti.

Numericamente i metodi maggiormente utilizzati per risolvere i problemi a valori iniziali sono:

• Metodi di Runge-kutta:
• Metodi predictor-corrector

Nella routine Ode45 è implementato il metodo di Runge-Kutta-Fehlberg, basato sul calcolo di due valori RK di ordine differente e sulla sottrazione dei risultati per arrivare ad una stima dell'errore. Questa tecnica porta alla seguente formula del quarto ordine:

unitamente alla formula del quinto ordine: con:

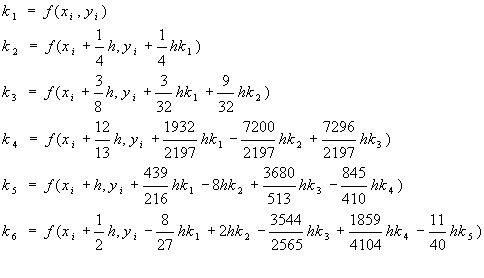
L'errore ricavato sottraendo la (8.1) alla (8.2), è il seguente:

E' possibile dunque risolvere un'equazione differenziale ordinaria con la (8.1) e ottenere una stima dell'errore con la (8.3).