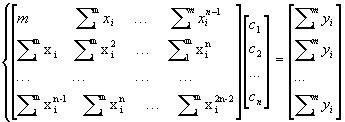Capitolo 4

Il problema dell'approssimazione di funzioni, d'importanza fondamentale nella matematica applicata, consiste nella sostituzione di una funzione complicata con una più semplice, scelta nell'ambito di una fissata classe di funzioni a dimensione finita.

Una tipica situazione in cui si presenta un'operazione di questo tipo è la seguente: la funzione da approssimare non è nota, ma di essa si conoscono alcuni valori su un insieme di punti e si vogliono avere indicazioni sul comportamento della funzione in altri punti. E' il caso di funzioni date in forma tabellare, corrispondenti, ad esempio, a dati sperimentali. In queste situazioni, approssimare una funzione, significa darne un modello rappresentativo.

In base al tipo e alla quantità dei dati, e alle caratteristiche del problema, si può scegliere tra due differenti approcci. Il primo, assumendo esatti i dati, cerca di costruire la curva che passi per certi punti assegnati (interpolazione), il secondo, invece, suppone i dati affetti da errore e cerca di costruire una curva che si scosti poco dai dati, in modo da non perdere le informazioni in essi contenute (smooting).

In generale un problema di interpolazione è posto nei seguenti termini: dati n punti distinti x_i si vuole determinare una funzione f(x) che in essi soddisfi m condizioni di interpolazione (vincoli che la funzione e/o le sue derivate devono soddisfare nei punti x_i). Nel caso in cui le condizioni sono f(x_i)=y_i, con y_i valori assegnati, per i=1,...,n, si parla di interpolazione di Lagrange. Se poi la funzione f è supposta appartenente ad uno spazio vettoriale a dimensione finita il problema è detto d'interpolazione lineare, e si riconduce alla determinazione delle componenti nella base prescelta (es. polinomi, funzioni trigonometriche, esponenziali, ecc.).

Storicamente le funzioni interpolanti più note e utilizzate sono state i polinomi, perché di facile valutazione, facilmente sommabili, integrabili e derivabili. Si ricorre, allora, frequentemente all'interpolazione polinomiale, senza tener conto, però del fatto che i polinomi hanno dei problemi d'efficienza ed accuratezza, in quanto presentano delle forti oscillazioni tra i dati. Questo problema pone dei limiti nella scelta dei polinomi, che in generale non superano l'ottavo-nono grado, cioè si usano polinomi che al massimo interpolano nove-dieci punti.

Nel caso in cui ci si trovi di fronte a problemi d'interpolazione con un numero elevato di punti, a causa della scarsa efficienza del modello polinomiale, la funzione interpolante è cercata in una classe più ampia, che include quella dei polinomi. Si tratta delle funzioni interpolanti a tratti, definite su di un numero finito e contiguo d'intervalli, in ognuno dei quali coincidono con un polinomio. In particolare, le funzioni polinomiali a tratti di grado m sono polinomi di grado m in ogni sottointervallo. Se queste funzioni presentano il pregio d'essere meno oscillanti, tuttavia, potrebbero non essere regolari in tutto l'intervallo di definizione, potrebbero ad es. avere derivate discontinue nei punti d'interpolazione.

Il compromesso si può raggiungere tramite particolari funzioni polinomiali a tratti di grado m, che comprendono i polinomi, si tratta delle funzioni spline di grado m. Le funzioni appartenenti a questa classe sono continue con le loro derivate fino a quella d'ordine m-1. Le più impiegate nelle applicazioni, sono le spline cubiche (o di terzo grado).

Le tecniche d'approssimazione di funzioni non si esauriscono con l'interpolazione. Quando i dati (x_i, y_i) sono in numero m elevato o affetti da errore (es. misurazioni sperimentali o indagini statistiche) non è ragionevole forzare la funzione a passare esattamente per gli m punti, ma è più conveniente effettuare uno smooting, cioè una "levigatura", al fine di minimizzare l'errore contenuto nei dati.

La risoluzione di tale problema richiede la scelta del tipo di funzione approssimante (modello) f(x), e di una misura del suo scostamento dai dati. Anche se la scelta del modello dipende generalmente dalle informazioni che si hanno sul problema, solitamente si adoperano modelli lineari, per la loro efficienza computazionale, e in particolare i polinomi p_n-1 = c₁+c ₂x +...+ c_nx^n-1

Per quanto riguarda la misura dello scostamento dai dati, si usa, generalmente, il residuo, cioè il vettore di componenti r_i= y_i- f(x_i), i=1,...,m. Quando si cerca una funzione tale da minimizzare la norma 2 del residuo, definita come:

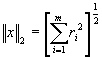
ciò equivale a minimizzare il quadrato di tale norma, e si parla, allora, di problema di minimi quadrati. Nel caso in cui la funzione f(x) è il polinomio p_n-1(x) (polinomio di minimi quadrati di grado n-1), l'imposizione delle condizioni di minimo (grad E=0) alla funzione porta alla risoluzione del sistema di equazioni normali: che fornisce i coefficienti (c₁,c₂…,c_n) del polinomio che realizza la migliore approssimazione del modello prescelto.