Parte terza: Matrici sparse non strutturate

Sspar

Scopo:	risoluzione di un sistema lineare sparso con matrice dei coefficienti non strutturata.
Specifiche:	subroutine sspar(r, c, irc, nrc, n, b, tolr, resr, nmax, x0, x, ifail) integer nrc, n, c(nrc), irc(n+1), nmax, ifail real r(nrc), tolr, resr, b(n), x0(n), x(n)
Descrizione:	Backgroud del problema In alternativa ai metodi diretti, per la risoluzione di sistemi lineari con matrice dei coefficienti di ordine elevato e sparsa, si possono applicare i metodi iterativi. La loro caratteristica fondamentale è quella di preservare la struttura della matrice, sfruttandone, quindi meglio l'eventuale sparsità. In generale un metodo iterativo si può esprimere come: dove B è una matrice detta di iterazione e c è un vettore, questo metodo è detto stazionario, in quanto la matrice B è costante ad ogni passo, del primo ordine, poiché x^(k+1) dipende solo da x^(k). I problemi fondamentali da risolvere sono quindi: effettuazione di una opportuna scelta della matrice B e del vettore c in modo tale che ogni soluzione di x = Bx +c sia anche soluzione di Ax=b (consistenza del metodo) determinazione delle condizioni affinché la successione generata dal metodo sia convergente per ogni scelta della stima iniziale. 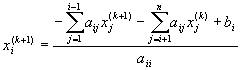L'idea del metodo Gauss-Seidel è la seguente: data una stima iniziale x0 della soluzione del sistema, si costruisce una successione di vettori {x^(k)} determinata dalla seguente relazione ricorrente con a_{ii ¹} 0, i=1, .., n, k =0, 1,2,... Descrizione dell'algoritmo Dopo aver controllato la correttezza dei dati in input e la compatibilità del sistema inserito, che equivale al controllare che la matrice dei coefficienti del sistema non abbia elementi nulli sulla diagonale, l'algoritmo parte con un costrutto iterativo che termina in tre eventualità, due coincidenti con la convergenza dell'algoritmo ed una coincidente con il raggiungimento del numero massimo di iterazioni consentite dall'utente. Al primo passo di iterazione si considera una stima iniziale della soluzione, corrispondente in questo caso ad un vettore nullo (x0), che con il procedere dei passi di iterazione è aggiornata con una nuova stima (x). I test sulla convergenza del metodo sono due. Si verifica che il rapporto (x-x0)/x, cioè la distanza relativa tra i valori della soluzione ottenuti con due successive iterazioni, sia minore della tolleranza relativa sulla soluzione inserita dall'utente, e che il rapporto (b-Ax)/b, cioè una misura di quanto la soluzione corrente soddisfi il problema numerico, sia minore della maggiorazione del residuo relativo del sistema inserito dall'utente. Se si verifica uno di questi due casi, allora l'algoritmo termina riportando in uscita la soluzione contenuta in x. Raccomandazioni sull'uso Per il funzionamento della subroutine, la matrice inserita non deve contenere elementi diagonali nulli. La matrice A (sparsa) dei coefficienti del sistema deve essere inserita sotto forma di tre vettori (r, c, irc) contenenti: r - gli elementi non nulli della matrice A c - il k-esimo elemento di c contiene l'indice di colonna del k-esimo elemento di r irc - il j-esimo elemento di irc contiene la posizione in r e c del primo elemento non nullo e del suo indice di colonna della j-esima riga di A, mentre il suo ultimo elemento contiene il numero di elementi di r aumentato di uno. L'ordine del sistema, il numero degli elementi non nulli della matrice A devono essere positivi. Il vettore dei termini noti deve essere lungo quanto l'ordine del sistema. La tolleranza relativa richiesta e la maggiorazione del residuo relativo del sistema devono essere positivi e minori di uno. Il numero massimo di iterazioni deve essere positivo. L'approssimazione iniziale della soluzione deve essere un vettore lungo quanto l'ordine del sistema e pu� essere costituito da numeri casuali.
Bibliografia:	[1], [2]
Parametri di I/O:	input r - vettore di reali, elementi non nulli della matrice c - vettore di interi, indici di colonna degli elementi di r irc - vettore di interi, posizioni in r e c n - intero, ordine del sistema nrc - intero, numero di elementi non nulli b - vettore di reali, termini noti del sistema tolr - reale, tolleranza relativa della soluzione resr - reale, maggiorazione del residuo nmax - intero, massimo numero di iterazioni x0 - vettore di reali, approssimazione iniziale output x - vettore di reali, soluzione del sistema ifail - intero, indicatore d'errore
Indicatori d'errore:	Errori gestiti dalla subroutine: ifail = 0 nessun errore ifail = 3 due casi possibili: ordine del sistema o numero di elementi non nulli, non positivi ifail = 1 due casi possibili: tolleranza relativa o maggiorazione del residuo non appartenenti all'intervallo [0,1[ ifail = 10 la matrice inserita ha almeno un elemento diagonale nullo ifail = 9 � stato raggiunto il numero massimo di iterazioni consentite
Routines ausiliarie:	tolm, funzione reale, tolleranza relativa
Tempo d'esecuzione:	se la matrice dei coefficienti del sistema Ann ha p coefficienti non nulli per riga e k � il numero di iterazioni eseguite, la complessit� di tempo � O(pn*k).
Memoria richiesta:	in memoria sono allocati sei array, di cui tre sono lunghi n, uno � lungo n+1 e due sono lunghi in modo proporzionale agli elementi non nulli della matrice.
Accuratezza fornita:	metodo esatto a meno del condizionamento della matrice e degli errori di round-off
Esempio di programma chiamante:	Program sspard c programma dimostrativo della subroutine sspar external sspar integer dim,nnz parameter (dim=10, nnz=20) integer nrc,n,c(nnz),irc(dim+1),nmax,ifail real r(nnz),b(dim),tolr,resr,x0(dim),x(dim) character12 fin,fout print,'* PROGRAMMA DIMOSTRATIVO DELLA SUBROUTINE SSPAR ' print write(,20)'Ordine del sistema (max ',dim,')= ' read(,)n write(,20)'Numero di elementi non nulli (max ',nnz,')= ' read(,)nrc print,'Tolleranza relativa per la soluzione= ' read(,)tolr print,'Residuo relativo= ' read(,)resr print,'Numero massimo di iterazioni= ' read(,)nmax print,'Nome del file di input= ' read(,'(A)')fin open(11,FILE=fin,STATUS='OLD') read(11,) do 1 i=1,nrc read(11,)r(i) 1 continue do 2 i=1,nrc read(11,)c(i) 2 continue do 3 i=1,n+1 read(11,)irc(i) 3 continue do 4 i=1,n read(11,)b(i) 4 continue close(11) do 10 i=1,n x0(i)=0 10 continue call sspar(r,c,irc,n,nrc,b,tolr,resr,nmax,x0,x,ifail) if (ifail .eq. 1) stop 'Errore! dimensione non valida' if (ifail .eq. 2) stop 'Errore! tolleranza relativa non valida' if (ifail .eq. 3) stop 'Errore! elemento diagonale nullo' if (ifail .eq. 4) print,'Attenzione! calcolo interrotto per ', % 'raggiungimento del numero massimo di iterazioni' print,'Nome del file di output= ' read(,'(A)')fout open(12,FILE=fout) write(12,30)(x(i),i=1,n) close(12) print,'Soluzione del sistema=' write(*,30)(x(i),i=1,n) 20 format(1X,A,I3,A) 30 format(1X,E14.7) End