Precedente Indice Successivo



Parte prima - Interpolazione



Conwt


Scopo: calcolo dei coefficienti del polinomio interpolante n punti assegnati, rappresentato nella forma di Newton.
Specifiche: subroutine conwt(x, y, n, ifail)
integer n, ifail
real x(n), y(n)
Descrizione: Backgroud del problema

Dati n punti xi e n valori corrispondenti yi, esiste un unico polinomio interpolante tali punti. La sua rappresentazione però non è unica, ma dipende dalla base scelta nello spazio vettoriale dei polinomi di grado £ n-1. Una rappresentazione particolarmente conveniente da un punto di vista computazionale è la seguente: pn-1(x) = an + an-1(x-xn) + an-2(x-xn)(x-xn-1) + ... + a1 (x-xn)...(x-x2), detta formula di Newton. Indicati, infatti, i coefficienti ai con y[xi,..., xi+k], essi si possono ottenere mediante la seguente formula ricorsiva:

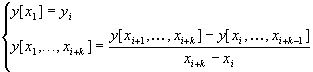
dove y[xi,...,xi+k] èdetta differenza divisa di ordine k relativa ai nodi xi, ... ,xi+k.

Descrizione dell'algoritmo

L'algoritmo, dopo il controllo dell'assenza di ascisse uguali, implementa, con uno schema iterativo, la formula per il calcolo delle differenze divise, memorizzando le stesse nel vettore contenente le ordinate dei punti di interpolazione.

Raccomandazioni sull'uso

Il numero di punti d'interpolazione deve essere positivo e minore di nove, inoltre le ascisse di tali punti devono essere distinte. Nel caso in cui il numero di punti è maggiore di nove, si suggerisce la risoluzione del problema utilizzando le subroutine cospl, pmq1, pmq2. I coefficienti sono memorizzati nel vettore delle ordinate dei punti d'interpolazione, quindi, se s'intende riutilizzare tale vettore è necessario eseguirne prima una copia.

Bibliografia: [1], [2]
Parametri di I/O: input

x - vettore di reali, ascisse dei punti d'interpolazione
y - vettore di reali, ordinate dei punti d'interpolazione
n - intero, numero dei punti d'interpolazione

output

y - vettore di reali, coefficienti del polinomio
ifail - intero, indicatore d'errore

Indicatori d'errore: Errori gestiti dalla subroutine:
ifail = 0 nessun errore.
ifail = 11 il numero dei punti è o non positivo, o maggiore di 9.
ifail = 12 sono state immesse almeno due ascisse uguali.
Routines ausiliarie: nessuna.
Tempo d'esecuzione: l'algoritmo calcola n(n-1)/2 differenze divise, ognuna delle quali richiede 2 somme e 1 prodotto, la complessità asintotica è O(3/2 n2)
Memoria richiesta: in memoria sono allocati due array di reali in singola precisione, di dimensione n, quindi, la complessità asintotica è O(2n).
Accuratezza fornita: funzione della precisione del sistema aritmetico.
Esempio di programma chiamante: 
      Program conwtd

c     Programma dimostrativo della subroutine conwt
 
      external conwt
      
      integer dim
      parameter (dim=10)
      
      integer n,ifail
      real x(dim),y(dim),a(dim)
      character*12 fin,fout

      print*
      print*,'*** PROGRAMMA DIMOSTRATIVO DELLA subROUTINE CONWT ***'
      print*
      write(*,10)'Numero di punti di interpolazione (max ',dim,')= '
      read(*,*)n
      
      print*,'Nome del file di input= '
      read(*,'(A)')fin
      open(11,FILE=fin,STATUS='OLD')
      do 1 i=1,n
         read(11,*)x(i)
    1 continue      
      read(11,*)
      do 2 i=1,n
         read(11,*)y(i)
    2 continue
      close(11)

      call conwt(x,y,n,a,ifail)

      if (ifail .eq. 11) stop 'Errore! numero di punti non valido'
      if (ifail .eq. 12) stop 'Errore! ascisse coincidenti'
      
      print*,'Nome del file di output= '
      read(*,'(A)')fout
      open(12,FILE=fout)
      write(12,'(E14.7)')(a(i),i=1,n)
      close(12)

      print*,'Coefficienti del polinomio interpolante ='
      write(*,'(E14.7)')(a(i),i=1,n)
   
   10 format (1X,A,I3,A)

      End


Precedente Indice Successivo