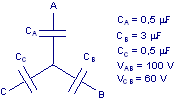Fisica

      

 

Costanti Fisiche

Unità Misura

Esercizi Fisica

Applet Java

 Test

Quesiti

  
 

Condensatori                                       

 
               
 

Esercizio n. 1

            
 

Due condensatori, C1 = 5,00 μF e C2 = 12,0 μF, sono collegati in parallelo e connessi ad una batteria di 9,00 V.
a)  Qual è il valore della capacità equivalente.
b)  Qual è la differenza di potenziale ai capi di ciascun condensatore.
c)  Qual è la carica immagazzinata in ciascun condensatore.

  
 

R.: 17 μF ;  9,0 V ; 45 μC ; 108 μC ;

 

  
               
 

Esercizio n. 2

            
 

Due condensatori, C1 = 5,00 μF e C2 = 12,0 μF, sono collegati in serie e connessi ad una batteria di 9,00 V.
a)  Qual è il valore della capacità equivalente.
b)  Qual è la differenza di potenziale ai capi di ciascun condensatore.
c)  Qual è la carica immagazzinata in ciascun condensatore.

  
 

R.: 3,53 μF ; 6,35 V ; 2,65 V ; 31,76 μC ;

  
               
 

Esercizio n. 3

            
 

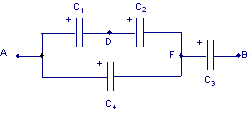
Quattro condensatori, C1 = 15,0 μF , C2 = 3,00 μF , C3 = 20,0 μF C4 = 6,00 μF , sono collegati come in figura. Trovare:
a)  La capacità equivalente fra i punti A e B.
b)  La carica di ciascun condensatore se ΔVAB = 15,0 V.
 

  
 

R.: 5,96 μF ; 26,3 μF ; 26,3 μF ; 89,4 μF ; 63,12 μF ;

  
               
 

Esercizio n. 4

            
 

Due condensatori quando sono collegati in parallelo hanno una capacità equivalente Cp e quando sono collegati in serie una capacità equivalente Cs.
Qual è la capacità di ciascun condensatore?

  
 

 
               
 

Esercizio n. 5

            
 

Si consideri il circuito di figura dove C1 = 6,00 μF, C2 = 3,00 μF e ΔV = 20,0 V. Dapprima si carica C1 chiudendo l’interruttore S1. Poi S1 viene aperto e il condensatore carico viene collegato a quello scarico chiudendo l’interruttore S2. Calcolare la carica iniziale di C1 e la carica finale di entrambi i condensatori.

  
 

R.: 120 μF ; 80 μF ; 40 μF ;

  
               
 

Esercizio n. 6

            
 

Tre capacità sono collegate alla batteria come mostrato in figura. Le capacità sono C1 = 3∙C , C2 = C , C3 = 5∙C.
a)  Determinare la capacità equivalente del sistema di condensatori.
b)  Ordinare le capacità, dalla più grande alla più piccola, in funzione della carica accumulata.
c)  Ordinare le capacità, dalla più grande alla più piccola, in funzione della d.d.p.
d)  Se C3 viene aumentata, cosa accade alle cariche immagazzinate negli altri condensatori?
 

  
 

R.: 2∙C ; Q1 , Q3 , Q2 ; ΔV1 , ΔV2 = ΔV3 ; C1 e C3 aumentano , C2 diminuisce ;

 
               
 

Esercizio n. 7

            
 

Nel progetto del circuito elettrico che regola le porte di un ascensore, il sistema di ritardo per la chiusura delle porte è previsto che abbia una capacità C = 32,0 μF tra A e B. Quando il circuito è stato costruito è stato istallato invece un condensatore economico ma al contempo molto resistente di capacità C1 = 34,8 μF. Per soddisfare le specifiche di progetto si può aggiungere un condensatore addizionale C2 fra i due punti. Esso dovrebbe essere posto in serie o in parallelo al condensatore C1? Quale dovrebbe essere il valore della capacità C2? Se il circuito ottenuto ha invece una capacità C = 29,8 μF tra A e B , quale ulteriore capacità deve essere istallata, in serie o in parallelo?

  
 

R.: 398 μF ; 2,20 μF ;

  
               
 

Esercizio n. 8

            
 

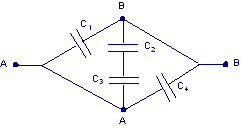
Trovare la capacità equivalente fra i punti A e B del collegamento di condensatori mostrato in figura dove i valori sono: C1 = 4,0 μF , C2 = 7,0 μF , C3 = 5,0 μF , C4 = 6,0 μF.

  
 

R.: 12,9 μF ;

  
               
 

Esercizio n. 9

            
 

a) Un condensatore di C = 3,00 μF è collegato ad una batteria di 12,0 V. Quanta energia è immagazzinata nel condensatore?
b) Se il condensatore fosse stato collegato ad una batteria di 6,00 V, quanta energia avrebbe immagazzinato?

  
 

R.: 216 μJ ; 54 μJ ;

  
               
 

Esercizio n. 10

            
 

La causa diretta di molti decessi è la fibrillazione ventricolare, un battito scoordinato del cuore che si oppone al battito proprio. Una scossa elettrica al torace può causare il momentaneo arresto del muscolo cardiaco, dopo il quale talvolta il cuore parte di nuovo con un battito regolare. Un defibrillatore è un dispositivo che applica una intensa scarica elettrica al torace per alcuni millisecondi. Il dispositivo contiene un condensatore di alcuni microfarad, caricato con alcune migliaia di volt. Due elettrodi di forma appropriata di circa 8 cm di sezione e rivestiti di una pasta conduttrice, sono premuti contro il torace su ambedue i lati del cuore. I loro manici sono isolati per evitare danni all’operatore, che dice “libero” (significando che nessuno deve toccare il paziente) e preme un pulsante per scaricare il condensatore attraverso il petto del paziente.
Si assuma che un’energia di 300 J venga liberata da un condensatore di 300 μF.
A quale differenza di potenziale è stato caricato?

  
 

R.: 4,5 kV ;

  
               
 

Esercizio n. 11

            
 

Due condensatori, C1 = 25,0 μF e C2 = 5,0 μF, sono collegati in parallelo e caricati con un alimentatore ΔV = 100 V.
a)  Disegnare un diagramma circuitale e calcolare l’energia totale accumulata nei due condensatori.
b)  Quale differenza di potenziale è necessaria ai capi degli stessi due condensatori collegati in serie, affinché l’energia sia la stessa del caso precedente. Disegnare un diagramma di questo circuito.

  
 

R.: 0,150 J ; 268 V ;

 
               
 

Esercizio n. 12

            
 

Un condensatore a facce piane e parallele con una capacità C = 3,6∙10−7 F viene caricato da un generatore di d.d.p. ad una tensione  V = 8,0 V, che poi viene staccato.
Successivamente si spostano le piastre in modo da avere una distanza pari a 4,5 volte quella iniziale.

Si determini la carica elettrica e la d.d.p. del condensatore nella nuova configurazione.

  
 

R.: 2,88∙10−6 C ; 36 V ;

 
               
 

Esercizio n. 13

            
 

Un condensatore di capacità C1 = 4,8∙10−6 F viene caricato ad una d.d.p. V = 45,0 V. Il generatore di tensione viene poi staccato. Il condensatore viene quindi collegato in parallelo ad un secondo condensatore di capacità C2 = 5,4∙10−7 F inizialmente scarico. Si calcoli la d.d.p. e la carica sul secondo condensatore.

  
 

R.: 40,449 V ; 2,1843∙10−5 C ; 

 
               
 

Esercizio n. 14

            
 

Un condensatore di capacità C1 = 6,4∙10−6 F viene caricato ad una d.d.p. V = 39,0 V. Il generatore di tensione viene poi staccato. Il condensatore viene quindi collegato in parallelo ad un secondo condensatore di capacità C2 = 6,6∙10−7 F inizialmente scarico. Si calcoli la d.d.p. e variazione di energia elettrostatica immagazzinata nel sistema.

  
 

R.: 35,354 V ; –4,5503·10−5 J ;

 
               
 

Esercizio n. 15

            
 

Due condensatori di capacità C1 = 2,0∙10–9 F e C2 = 7,6∙10–8 F vengono caricati entrambi con 2 generatori di tensione che forniscono una d.d.p. V = 10.0 V, ma con polarità opposte. I generatori di tensione vengono poi staccati. I due condensatori vengono quindi collegati fra loro con dei sottili fili conduttori in modo che la piastra positiva di uno sia collegata alla piastra negativa dell’altro. Si determini la d.d.p. finale, la carica finale di C1.
 

  
 

R.: –9,4872 V ; –1,8974·10–8 C ;

 
               
 

Esercizio n. 16

            
 

Due condensatori di capacità C1 = 2,4∙10–9 F e C2 = 9,0∙10–8 F vengono caricati entrambi con 2 generatori di tensione che forniscono una d.d.p. V = 12.5 V, ma con polarità opposte. I generatori di tensione vengono poi staccati. I due condensatori vengono quindi collegati fra loro con dei sottili fili conduttori in modo che la piastra positiva di uno sia collegata alla piastra negativa dell’altro. Si determini la d.d.p. finale e la variazione di energia elettrostatica del sistema fra la configurazione finale e quella iniziale.

  
 

R.: –11,851 V ; –7,3014∙10–7 J ;

 
               
 

Esercizio n. 17

            
 

Un condensatore a facce piane e parallele di capacità C = 4,2∙10−6 F viene caricato con un generatore che fornisce una d.d.p. V = 11,0 V. Poi viene scollegato dal generatore, e viene inserita fra le piastre una lastra di materiale dielettrico (ε r = 3,0) che riempie completamente lo spazio tra le armature. Si determini la carica e la d.d.p sul condensatore nella configurazione finale.

  
 

R.: 4,62∙10−5 C ; 3,6667 V ;

 
               
 

Esercizio n. 18

            
 

Un condensatore a facce piane e parallele di capacità C = 2,8∙10−6 F viene inserita una lastra di materiale dielettrico (ε r = 2,5) che riempie completamente lo spazio tra le armature. Poi il condensatore viene collegato ad un generatore che fornisce una d.d.p. V = 14,0 V. Si estrae quindi completamente la lastra di materiale dielettrico. Si determini la carica e la variazione di energia immagazzinata nel condensatore.

  
 

R.: 3,92∙10−5 C ; –4,116∙10−4 J ;

 
               
 

Esercizio n. 19

            
 

Si calcoli la capacità di un condensatore costituito da due dischi metallici di raggio R = 10 cm, posti ad una distanza d = 0,6 cm e separati da un dielettrico con ε r = 3,5.
Si calcoli, inoltre, il campo elettrico e l’energia elettrostatica accumulata nel condensatore se tra le sue armature vi è una differenza di potenziale ΔV = 1500 V.

  
 

R.: 1,62∙10–10 F ; 250∙103 V/m ; 1,82∙10–4 J ;

 
               
 

Esercizio n. 20

            
 

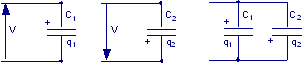
Due condensatori isolati di capacità C1 = 1 μF e C2 = 0,5 μF sono caricati con d.d.p. ΔV1 = 50 V e ΔV2 = 150 V rispettivamente. Calcolare la variazione di energia elettrostatica se essi vengono collegati in parallelo connettendo le due armature positive tra loro.

  
 

R.: –1,67∙10–3 J ;  

  
               
 

Esercizio n. 21

            
 

Un condensatore piano con armature di area A = 500 cm2, distanti fra loro d = 1,2 cm è caricato ad una d.d.p. ΔV = 60 V. Le due armature vengono poi allontanate fino a che la distanza diventa d’ = 3 cm. Calcolare la d.d.p. finale ed il lavoro per muovere le armature.

  
 

R.: 150 V ; 0,996∙10–7 J ;  

  
               
 

Esercizio n. 22

            
 

Un condensatore piano è costituito da due armature di area S = 80 cm2, poste ad una distanza d = 1,0 cm. Fra di esse viene inserita:
a)  Una lastra metallica di spessore a = 2,5 mm.
b)  Una lastra di vetro (ε r = 4,5) di spessore a = 3,0 mm.
Trascurando gli effetti ai bordi, calcolare, nei due casi, la capacità e la densità di carica sulle armature del condensatore, se esso viene caricato a 1000 V.

  
 

R.: 9,44∙10–12 F ; 9,24∙10–12 F ; 1,18∙10–6 C/m2 ; 1,15∙10–6 C/m2 ;  

  
               
 

Esercizio n. 23

            
 

Si trovi il valore della capacità da assegnare a C1 affinché la tensione ai morsetti del condensatore C2 sia V2 = 100 V.

 

  
 

R.: 526,3 μF ;  

  
               
 

Esercizio n. 24

            
 

Tre capacità sono collegate come in figura.
Conoscendo VAB = 100 V e VCB = 60 V, calcolare la carica su ciascuna capacità.

 

  
 

R.: 40 μC ; 60 μC ; 20 μC ;

 
               
 

Esercizio n. 25

            
 

Cinque condensatori uguali sono collegati come in figura.
Si trovi il valore della d.d.p. ai capi di C1 sapendo che fra i punti A e B la d.d.p. vale VAB = 200 V.
 

  
 

R.: 100 V ;

  
               
 

Esercizio n. 26

            
 

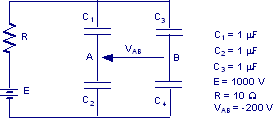
Trovare il valore da assegnare alla capacità C4 affinché, a regime, la d.d.p. VAB = – 200 V.

 

  
 

R.: 0,429 μF ;