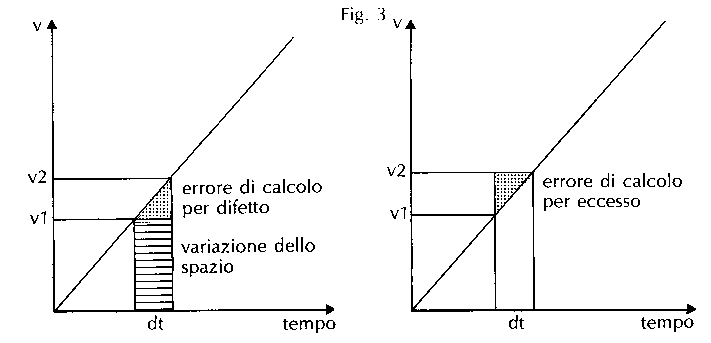
In maniera analoga si può procedere per la velocità:
v = (s2-s1)/(t2-t1)
quindi:
dt·v = s2-s1
s2 = s1 + v·dt
cioè lo spostamento al tempo t2 è dato dallo spostamento al tempo t1 più la velocità per l'intervallo di tempo.
Questa formula è approssimata se la velocità varia. Ma essa è tanto più precisa quanto più piccolo sarà l'intervallo scelto dt.

Nel caso in cui il moto di un particolare oggetto avviene in un piano, si possono scomporre accelerazione, velocità e posizione lungo gli assi:
vx2 = vx1 + ax·dt vx = vx + ax*dt
vy2 = vy1 + ay·dt vy = vy + ay*dt
x2 = x1 + vx·dt x = x + vx*dt
y2 = y1 + vy·dt y = y + vy*dt
in Python
Come si vede
l'operatore
assegnazione del Python permette di scrivere in maniera molto
espressiva
queste definizioni fisiche di accelerazione e velocità.
Così
ad esempio la prima assegnazione dice che la velocità finale
è
data dalla velocità iniziale più il prodotto della
accelerazione
per l'intervallino di tempo dt.
Come esempio di
calcolo
ricorrente si può eseguire il programma sui rimbalzi
di una palla (listato).