Prendiamo in considerazione la definizione di accelerazione.
Abbiamo un' accelerazione quando si verifica una variazione del vettore velocità al variare del tempo:
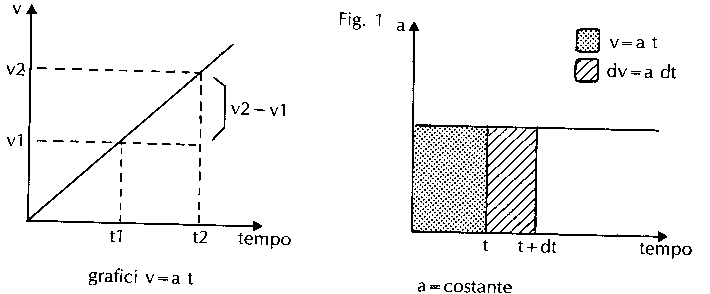
a = (v2-v1)/(t2-t1)
cioè l'accelerazione (in modulo) è data dal rapporto fra la variazione della velocità v2-v1 e il corrispondente intervallo di tempo trascorso t2-t1. Indicando con dt questo intervallo, ponendo cioè dt = t2-t1, si ha:
dt·a=v2-v1
ovvero
v2 = v1 + a·dt
che si può spiegare dicendo che la velocità ad un certo istante è data dalla velocità posseduta precedentemente più il prodotto della accelerazione per l'intervallo di tempo trascorso.
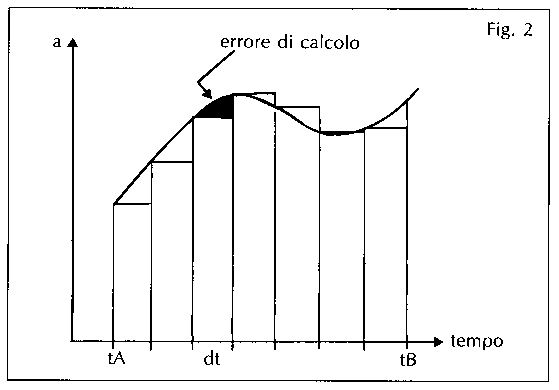
Questo è rigoroso per l'accelerazione media o quando essa è costante, ma è approssimativamente valido, anche quando l'accelerazione non è costante, qualora si prenda un intervallo di tempo molto piccolo.
Conoscendo l'accelerazione a e la velocità v1 al tempo t1 è possibile trovare la velocità dopo un intervallo di tempo dt in maniera tanto più precisa tanto più piccolo è il valore di dt perchè tanto più piccolo è dt tanto più piccola sarà la variazione della accelerazione in questo intervallo di tempo.

L`area del rettangolino di base dt rappresenta la variazione della velocità.
È sempre opportuno dare una interpretazione grafica della variazione della velocità per una migliore comprensione delle relazioni matematiche.