 |
(4.2.1) |
Il punto di partenza è sempre il sistema composto da sei lamine in configurazione tre lamine equivalenti.
Prima di tutto bisogna ricordare la definizione di DGD, che nello spazio dei vettori di Stokes risulta
 |
(4.2.1) |
L'espressione precedente può venir esplicitata nella forma
Ci si propone ora di calcolare la matrice di Müller risultante dal contributo degli ![]() cristalli birifrangenti, e da questa arrivare al calcolo della componenti del vettore
cristalli birifrangenti, e da questa arrivare al calcolo della componenti del vettore
![]() , da cui ricavare l'espressione del DGD derivato in
, da cui ricavare l'espressione del DGD derivato in
![]() .
.
Si ricordano le espressioni delle matrici di Müller, e altre espressioni necessarie a svolgere la teoria di Müller, nell'ordine: il vettore
![]() ,
,
 |
(4.2.4) |
la matrice
![]()
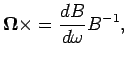 |
(4.2.5) |
![$\displaystyle \mathbf {\Omega \times}=\left[ \begin{array}{c c c} 0 & -\Omega_{...
...ga_{z} & 0 & -\Omega_{x} \ -\Omega_{y} & \Omega_{x} & 0 \ \end{array}\right],$](img224.png) |
(4.2.6) |
Dalla matrice di Müller e dalla matrice di rotazione i-esima si ottiene la matrice caratteristica della lamina i-esima
![]() , che descrive il comportamento della lamina nel sistema al variare della frequenza angolare e dell'angolo compreso tra gli assi di due lamine successive,
, che descrive il comportamento della lamina nel sistema al variare della frequenza angolare e dell'angolo compreso tra gli assi di due lamine successive,
Tenuto conto che il sistema in analisi è costituito da sei lamine, la matrice che descrive interamente il comportamento del sistema si otterrà come moltiplicazione di altrettante matrici della forma 4.2.9.
Tuttavia avendo ipotizzato una configurazione a tre lamine equivalenti, e avendo posto il primo banco di lamine a zero gradi, in modo da utilizzzarlo come riferimento per la rotazione dei blocchi successivi, la matrice di rotazione 4.2.8 per ![]() diventa la matrice identica, mentre il prodotto di due matrici nella forma 4.2.9 con
diventa la matrice identica, mentre il prodotto di due matrici nella forma 4.2.9 con
![]() mantiene ancora la forma di riferimento, tuttavia la matrice di Müller associata assume la forma:
mantiene ancora la forma di riferimento, tuttavia la matrice di Müller associata assume la forma:
In questo modo si è costruita quella che chiamiamo una lamina eqivalente, ossia la giustapposizione di due lamine con gli assi allineati, che nel caso ideale sarà descritta dalla relazione:
Dalla 4.2.11 risulta evidente che nel caso di perfetto allineamento delle due lamine, il comportamento della lamina equivalente coincide con quello di una singola lamina caratterizzata da
![]() nella forma 4.2.9.
nella forma 4.2.9.
Nell'ipotesi invece che l'allineamento non sia perfetto, e che le lamine adiacenti siano disallineate di un angolo ![]() , tale che
, tale che
![]() , il prodotto tra le matrici di rotazione non offre come risultato la matrice identica.
, il prodotto tra le matrici di rotazione non offre come risultato la matrice identica.
Pertanto nell'ipotesi di non perfetto allineamento delle lamine la matrice di Müller della lamina equivalente assume la forma
Dalle diverse matrici ![]() associate alle singole lamine o alle lamine equivalenti, si perviene alla matrice del sistema, nel formalismo di Müller, attraverso il semplice prodotto di matrici
associate alle singole lamine o alle lamine equivalenti, si perviene alla matrice del sistema, nel formalismo di Müller, attraverso il semplice prodotto di matrici
Risulta chiaro allora che si perviene al calcolo di
![]() attraverso la derivazione della matrice complessiva
attraverso la derivazione della matrice complessiva ![]() rispetto alla frequenza angolare e della matrice
rispetto alla frequenza angolare e della matrice
![]() rispetto a
rispetto a
![]() ; operazioni tutt'altro che agevoli vista la notevole complessità che possono raggiungere le espressioni.
; operazioni tutt'altro che agevoli vista la notevole complessità che possono raggiungere le espressioni.
In letteratura il problema della derivazione è stato in parte risolto adottando la seguente approssimazione
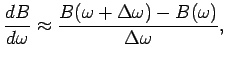 |
(4.2.16) |
Essendo la generica ![]() una funzione matriciale, si può applicare la nota regola di derivazione del prodotto di funzioni all'espressione 4.2.15 e si ottiene:
una funzione matriciale, si può applicare la nota regola di derivazione del prodotto di funzioni all'espressione 4.2.15 e si ottiene:
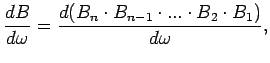 |
(4.2.17) |
Si osserva che la 4.2.18 è una formula ricorsiva, infatti possiamo riscriverla evidenziandone chiaramente la ricorsività intrinseca; definiamo dapprima la matrice complessiva
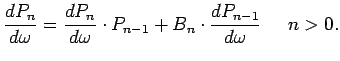 |
(4.2.20) |
Infatti per ![]() l'espressione 4.2.19 si riduce a
l'espressione 4.2.19 si riduce a
![$\displaystyle P_{n}=I_{3}=\left[\begin{array}{c c c} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ \end{array} \right] \;\;\;\;\; n=0 .$](img258.png) |
(4.2.21) |
Verificato che si può pervenire al calcolo preciso della derivata senza l'approssimazione incrementale diamo una traccia dei passaggi che portano alla sua implementazione iterativa. Nuovamente dall'espressione 4.2.15 per ![]() si ottiene
si ottiene
Sostituendo, per un sistema a tre lamine , le espressioni 4.2.22, 4.2.23 e 4.2.24 nella 4.2.19 si ottiene
![$\displaystyle \frac{d(B_{3} \cdot B_{2} \cdot B_{1})}{d \omega}=\frac{d B_{3}}{...
...d B_{2}}{d \omega} \cdot B_{1} + B_{2} \cdot \frac{d B_{1}}{d \omega} \right] .$](img264.png) |
(4.2.25) |
Come si può notare, il problema della derivazione esatta in ![]() del prodotto
del prodotto
Il calcolo della derivata della matrice ![]() di una singola lamina non rappresenta infatti una notevole difficoltà.
di una singola lamina non rappresenta infatti una notevole difficoltà.
Si consideri a tale proposito un generico cristallo birifrangente preso singolarmente, la sua matrice nel formalismo di Müller risulta
| (4.2.26) |
![$\displaystyle \begin{footnotesize}
B_{i}=\left[\begin{array}{c c c}
\par
\cos^{...
... \cos (\Delta \tau_{i} \omega) \\
\par
\end{array} \right]
\end{footnotesize}$](img267.png) |
(4.2.27) |
![$\displaystyle \begin{footnotesize}
\frac{d B_{i}}{d \omega}=\Delta \tau_{i} \le...
...-\sin (\Delta \tau_{i} \omega) \\
\par
\end{array} \right]
\end{footnotesize}$](img268.png) |
(4.2.28) |
A questo punto disponiamo di tutti gli elementi necessari per il calcolo della derivata rispetto a
![]() di
di
![]() ,
,
Sostituendo la 4.2.30 nell'espressione della derivata di
![]() 4.2.29 si ottiene
4.2.29 si ottiene
Infine, analogamente a quanto scritto nell'espressione 4.2.24, per un sistema a tre lamine, la derivata rispetto a
![]() diventa:
diventa:
![$\displaystyle \frac{\partial B }{\partial \Delta \tau_{i}}= \frac{\partial[B_{3...
...ta \tau_{i}} B_{1} + B_{2} \frac{\partial B}{\partial \Delta \tau_{i}} \right],$](img272.png) |
(4.2.32) |
Ugualmente, procedendo con le sostituzioni a ritroso, si possono calcolare le espressioni dei
![]() per
per ![]() nel sitema a tre lamine considerato.
nel sitema a tre lamine considerato.
Con un ragionamento analogo a quello svolto fin'ora riguardo la derivata del DGD rispetto
![]() , si può definire anche il rapporto
, si può definire anche il rapporto
![]() col significato di derivata del DGD rispetto al disallineamento all'interno della lamina equivalente i-esima.
col significato di derivata del DGD rispetto al disallineamento all'interno della lamina equivalente i-esima.