| (2.8.1) |
Le interpretazioni esposte nei paragrafi precedenti affrontano la PMD facendo uso di un modello in cui vengono definiti due autostati di polarizzazione e le costanti di propagazione dei due modi sono distinte quando viene meno la simmetria circolare del nucleo.
L'applicazione di questo modello alle fibre reali appesantisce notevolmente la trattazione in quanto l'orientazione aleatoria degli assi di birifrangenza impedisce l'identificazione degli autostati. Si mantiene solamente informazione riguardo l'evoluzione del vettore polarizzazione senza disporre di una base di riferimento univoca.
Viene dunque proposto un approccio di tipo fenomenologico che porterà a determinare una base conveniente per la descrizione delle caratteristiche della PMD in fibre di lunghezza e configurazione arbitraria.
Si può infatti dimostrare che per ogni mezzo trasmissivo ottico lineare privo di PDL (Polarization Dependent Loss) esistono due stati di polarizzazione ortogonali di ingresso cui corrispondono due stati di polarizzazione di uscita ortogonali e al primo ordine indipendenti dalla frequenza [4].
La relazione da cui si parte
precisando che
![]() tiene conto di attenuazione e ritardo di fase introdotti dalla fibra,
tiene conto di attenuazione e ritardo di fase introdotti dalla fibra, ![]() è la matrice unitaria che descrive il comportamento della fibra ed
è la matrice unitaria che descrive il comportamento della fibra ed
![]() rappresenta il campo in ingresso indipendente, dalla frequenza.
rappresenta il campo in ingresso indipendente, dalla frequenza.
Derivando la 2.8.1 rispetto ![]() ed esprimendo il campo in ingresso
ed esprimendo il campo in ingresso
![]() in funzione di
in funzione di
![]() si perviene all'equazione differenziale
si perviene all'equazione differenziale
Inoltre scrivendo il campo in forma complessa secondo
![]() , cioè rispetto al versore del campo elettrico
, cioè rispetto al versore del campo elettrico
![]() e sostituendo l'espressione nella precedente 2.8.2, si ottiene la derivata rispetto alla frequenza angolare del versore campo elettrico, nella forma
e sostituendo l'espressione nella precedente 2.8.2, si ottiene la derivata rispetto alla frequenza angolare del versore campo elettrico, nella forma
Si vogliono ora trovare due stati di polarizzazione al primo ordine indipendenti dalla frequenza angolare, che pertanto verificano la relazione
Dalla 2.8.3 è evidente che la condizione 2.8.4 è verificata se il determinante di
![]() risulta nullo ovvero, tenendo presente che in generale la matrice
risulta nullo ovvero, tenendo presente che in generale la matrice ![]() assume la forma
assume la forma
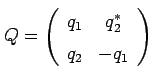 |
(2.8.5) |
Gli stati di polarizzazione che si ottengono sono chiamati PSP di uscita, acronimo per Principal States of Polarization, e coincidono con gli autovettori della matrice ![]() .
Da un punto di vista fisico si tratta di quegli stati di polarizzazione che sono, almeno al primo ordine, indipendenti dalla frequenza.
.
Da un punto di vista fisico si tratta di quegli stati di polarizzazione che sono, almeno al primo ordine, indipendenti dalla frequenza.
La condizione di dispersione zero negli stati di polarizzazione di uscita assicura che impulsi in ingresso con polarizzazione allineata ai corrispondenti autostati di ingresso si propaghino con durata invariata lungo la fibra. In secondo luogo l'ortogonalità dei PSP in ingresso e in uscita suggerisce di considerarli come una base di vettori per la descrizione del comportamento della fibra.
Questa descrizione tramite PSP appare analoga a quella proposta tramite gli autostati di polarizzazione nelle fibre corte eccetto che in luogo degli autostati si hanno i PSP. É importante sottolineare che i PSP non risentono della birifrangenza locale del mezzo ma in generale solamente dell'effetto globale di asimmetria della fibra sull'intera lunghezza considerata.
É facile notare inoltre che in assenza di accoppiamento dei modi, i PSP coincidono con gli autostati del sistema e che le due descrizioni coincidono.
Riscrivendo la relazione 2.8.6 sostituendo
![]() si perviene all'equazione
si perviene all'equazione
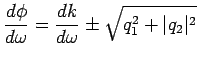 |
(2.8.7) |
Il modulo della differenza fra i tempi di arrivo delle onde che si propagano sui due assi viene indicato con l'acronimo DGD, per Differential Group Delay, e vale
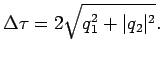 |
(2.8.8) |
Risulta chiaro allora che quando si lancia potenza su entrambi i PSP di un mezzo birifrangente, la PMD determina allargamento nell'impulso. Allargamento che risulta massimo quando la potenza si divide esattamente fra le due polarizzazioni. Nel caso invece lo stato di polarizzazione di ingresso coincida con uno dei PSP l'impulso di uscita sarà, al primo ordine, una copia ritardata di quello di ingresso. In realtà quando si lancia potenza su uno solo dei PSP l'impulso subisce un allargamento causato dalla dipendenza dalla frequenza, al secondo ordine, dei PSP.
Per creare un legame logico fra birifrangenza locale e PSP è opportuno utilizzare il formalismo delle matrici di Müller. Secondo il procedimento già seguito la relazione ingresso-uscita sulla sfera di Poincarè si può scrivere nella forma
| (2.8.9) |
Per il ragionamento illustrato nel paragrafo 2.7 esisterà un vettore
![]() tale che la 2.8.10 si possa scrivere nella forma
tale che la 2.8.10 si possa scrivere nella forma
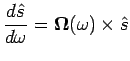 |
(2.8.11) |
 |
(2.8.12) |
Con un semplice calcolo si nota che il modulo di
![]() è pari al valore del DGD mentre la direzione individua i PSP.
è pari al valore del DGD mentre la direzione individua i PSP.
Per quanto detto si conclude che se il vettore di birifrangenza locale
![]() caratterizza l'evoluzione puntuale lungo
caratterizza l'evoluzione puntuale lungo ![]() degli autostati, il vettore
degli autostati, il vettore
![]() descrive le variazioni in frequenza degli stati di polarizzazione lungo tutta la lunghezza della tratta.
descrive le variazioni in frequenza degli stati di polarizzazione lungo tutta la lunghezza della tratta.