Rappresentazione mediante matrici di Müller

Partendo dalla relazione ingresso uscita dal mezzo dielettrico 2.6.3, e riportata sotto per comodità, ricordando la rappresentazione dei vettori di Stokes formulata nel paragrafo 2.2

$$\mathbf{e}(z)= U(z) \mathbf{e}_{0}$$ (2.7.1)

si può dimostrare che vale la seguente rappresentazione sulla sfera di Poincarè

$$\mathbf{s}(z)=R(z) \mathbf{s}_{0}$$ (2.7.2)

dove $R(z)$ risulta essere una matrice ortogonale, in quanto mantiene inalterato il modulo dei vettori nel campo reale, cioè $R^{-1} = R^{T}$, per la conservazione dell'energia in un mezzo senza perdite.

Il legame fra matrici ortogonali e matrici unitarie trova le sue radici nella dimostrazione analitica dell'isomorfismo fra il gruppo delle matrici unitarie ed il gruppo delle matrici ortogonali. In modo analogo al procedimento precedentemente svolto per le matrici di Jones, derivando in z la 2.7.2 si ottiene:

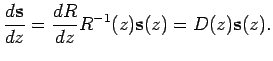$$\frac{d \mathbf{s}}{d z}=\frac{d R}{d z}R^{-1}(z) \mathbf{s}(z)=D(z) \mathbf{s}(z) .$$ (2.7.3)

Si perviene così a un nuovo formalismo per gestire l'equazione dei modi accoppiati nello spazio $R^{3}$ ma sempre in forma matriciale. Essendo $\mathbf{s}(z)$ vincolato a ruotare sulla sfera di Poincarè, esiste un vettore $\bar \beta(z)$ detto vettore di birifrangenza locale tale che

$$\frac{d \mathbf{s}}{d z} = \bar \beta(z) \times \mathbf{s}(z)$$ (2.7.4)

che ci aiuta a capire come la birifrangenza intrinseca del mezzo agisca sullo stato di polarizzazione.

Si consideri prima il caso in cui il vettore $\beta(z)$ sia costante; pertanto il vettore $\mathbf{s}(z)$ ruota attorno al vettore $\beta(z)$, eccetto il caso in cui $\mathbf{s}(z)$ risulti parallelo o antiparallelo al vettore $\beta(z)$, cioè quando la polarizzazione rimane invariata. La direzione del vettore $\beta(z)$ individua dunque gli autostati del sistema, ovvero gli stati di polarizzazione che si propagano invariati lungo la fibra. Il modulo del vettore $\beta(z)$ è invece da mettere in relazione con la lunghezza di battimento

$$L_{B}=\frac{2 \pi}{\vert\bar \beta \vert} .$$ (2.7.5)

Pertanto se il mezzo dielettrico in questione è debolmente birifrangente, come le comuni fibre ottiche per telecomunicazioni, $L_{B}$ assume valori tipici dell'ordine di qualche decina di metri, quindi si può ritenere che il sistema evolva lentamente attraverso i diversi stati di polarizzazione; se invece il mezzo è significativamente birifrangente, come nel caso delle fibre a mantenimento di polarizzazione, la $L_{B}$ risulta dell'ordine del millimetro, e l'evoluzione dello stato di polarizzazione è molto rapida.

Se invece il vettore $\beta$ non è costante sulle varie sezioni, come accade nelle comuni fibre, gli stati di polarizzazione evolvono in maniera casuale e gli autostati non rimangono fissi ma si scambiano potenza oppure originano fenomeni di battimento.

É possibile dimostrare che sussiste una relazione fra il vettore $\beta$ e gli elementi della matrice $B$ definita al 2.6.6, più esattamente vale la relazione:

$$\bar \beta=\left(\begin{array}{c} \Delta \beta \ 2 \Re(K) \ 2 \Im(K) \ \end{array} \right) .$$ (2.7.6)