Rappresentazione mediante matrici di Jones

Ora sarà discusso un modello per la descrizione della dispersione dei modi di polarizzazione che, sulla base di relazioni matriciali ingresso-uscita note per i componenti ottici, fornisce la matrice di birifrangenza della fibra. Si ritrovano le stesse conclusioni ottenute dal modello precedente, benchè in questo caso venga utilizzato un approccio differente.

Sia $T(z)$ la matrice che descrive il mezzo trasmissivo; la relazione ingresso-uscita viene scritta nella forma

$$y(z)=T(z)x=e^{\beta(z)}U(z)x$$ (2.6.1)

dove $\beta(z)$ rappresenta l'attenuazione locale del sistema. La matrice $U(z)$, conservando il modulo dei vettori nel campo complesso, risulterà unitaria ovvero $U^{-1} = U^{T*}$.

La forma generale di una matrice unitaria è

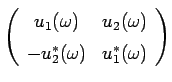$$\left( \begin{array}{c c} u_{1}(\omega) & u_{2}(\omega) -u_{2}^{*}(\omega) & u_{1}^{*}(\omega) \end{array} \right)$$ (2.6.2)

dove $\vert u_{1}\vert^{2} + \vert u_{2}\vert^{2} = 1$.

In base alle considerazioni svolte, lanciando un campo monocromatico in ingresso, nella forma $\mathbf{e}_{0}$, all'uscita del mezzo risulta

$$\mathbf{e}(z)= U(z) \mathbf{e}_{0} ,$$ (2.6.3)

dove per ipotesi si sta considerando un mezzo a perdite trascurabili, e un segnale in ingresso di ampiezza unitaria. Derivando la 2.6.3 rispetto a $z$ si ottiene

$$\frac{d \mathbf{e}}{d z}= \frac{d U}{d z}=\frac{d U}{d z} U(z)^{-1} \mathbf{e}(z) = -j B(z) \mathbf{e}(z) .$$ (2.6.4)

Dalle caratteristiche di $U(z)$ si può dimostrare che $B(z)$ ha la seguente forma

$$B(z)=\left( \begin{array}{c c} b_{1} & b_{2}^{*} b_{2} & -b_{1}^{*} \end{array} \right)$$ (2.6.5)

ed essendo costante il modulo di $\mathbf{e}(z)$ per la conservazione dell'energia in un mezzo non dissipativo, $b_1$ risulta reale, quindi la 2.6.5 può essere riscritta nelle forma

$$B(z)=\left( \begin{array}{c c} \frac{\Delta \beta}{2} & K^{*} \ K & -\frac{\Delta \beta}{2} \ \end{array} \right) ,$$ (2.6.6)

con $\Delta \beta=\omega \frac{\Delta n}{c}$ reale.

La matrice $B(z)$ fornisce le caratteristiche di birifrangenza indotta sul sistema alla stessa maniera dei coefficienti del modello dei modi accoppiati $k_{ij}$. Per rendersene conto è sufficiente confrontare la 2.6.4 con la 2.5.5.