La propagazione di un impulso in una fibra ottica può essere visto come la propagazione di un onda elettromagnetica lungo la direzione che indicheremo con ![]() .
Consideriamo due onde elettromagnetiche lineamente polarizzate e ortogonali tra di loro, che si propagano in direzione
.
Consideriamo due onde elettromagnetiche lineamente polarizzate e ortogonali tra di loro, che si propagano in direzione ![]() . Tali campi possono essere descritti con la notazione complessa nella forma:
. Tali campi possono essere descritti con la notazione complessa nella forma:
| (2.2.1) | |||
| (2.2.2) |
Il campo che si propaga pertanto è la sovrapposizione dei due campi ortogonali, cioè il vettore somma delle componenti ortogonali
| (2.2.3) |
Lo stato di polarizzazione può essere rappresentato con il vettore di Jones
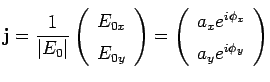 |
(2.2.4) |
Nel caso generico della polarizzazione ellittica il vettore di Jones assume la forma
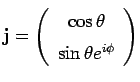 |
(2.2.5) |
L'effetto di far attraversare alla luce un mezzo birifrangente viene formalizzato usando la matrice
![]() nel campo complesso, che trasforma lo stato di polarizzazione in ingresso nello stato di uscita
nel campo complesso, che trasforma lo stato di polarizzazione in ingresso nello stato di uscita
 |
(2.2.6) |
Ogni vettore di Jones è caratterizzato da due angoli che in un sistema di coordinate sferiche individuano un generico punto sulla sfera di raggio unitario. Ogni stato di polarizzazione coincide con un punto della sfera unitaria, generalmente chiamata sfera di Poincarè.
![\includegraphics[width=100mm]{thesisSunnerud_4it.eps}](img71.png) |
Ogni punto della sfera, e quindi ogni stato di polarizzazione, può essere individuato anche attraverso una terna di vettori in un sistema di riferimento cartesiano, chiamati vettori di Stokes
In questo modo si fa corrispondere ad ogni punto della sfera un preciso stato di polarizzazione. La definizione al 2.2.7 nel dominio dei vettori complessi risulta più comprensibile se espressa in base agli angoli che il vettore polarizzazione forma con la base di versori che generano la sfera
![]() , in questo modo otteniamo la relazione al terzo membro che evidenzia la dipendenza delle componenti del vettore polarizzazione dagli angoli
, in questo modo otteniamo la relazione al terzo membro che evidenzia la dipendenza delle componenti del vettore polarizzazione dagli angoli ![]() e
e ![]() .
.
Gli stati a polarizzazione rettilinea sono localizzati sull'equatore della sfera, e pertanto caratterizzati da ![]() , invece gli stati rispettivamente a polarizzazione circolare destrorsa e sinistrorsa sono localizzati ai poli, e caratterizzati rispettivamente da
, invece gli stati rispettivamente a polarizzazione circolare destrorsa e sinistrorsa sono localizzati ai poli, e caratterizzati rispettivamente da ![]() e
e ![]() . Si evidenzia che nello spazio delle coordinate, stati a polarizzazionie ortogonale sono descritti da vettori antiparalleli, pertanto caratterizzati da vettori di polarizzazione tali che
. Si evidenzia che nello spazio delle coordinate, stati a polarizzazionie ortogonale sono descritti da vettori antiparalleli, pertanto caratterizzati da vettori di polarizzazione tali che
![]()
Il formalismo utilizzato è quello di Jones, che descrive il generico vettore di Stokes
![]() , in funzione dei due parametri
, in funzione dei due parametri ![]() e
e ![]() .
La notazione di Stokes prevede, oltre alle tre componenti vettoriali del vettore polarizzazione, un ulteriore parametro chiamato intensità ottica,
.
La notazione di Stokes prevede, oltre alle tre componenti vettoriali del vettore polarizzazione, un ulteriore parametro chiamato intensità ottica,
 |
(2.2.8) |
Per un campo completamente polarizzato infatti vale
![]() , pertanto il grado di polarizzazione (DOP) definito come
, pertanto il grado di polarizzazione (DOP) definito come
 assume in questo caso valore unitario.
assume in questo caso valore unitario.
![\includegraphics[width=80mm]{thesisSunnerud_5.eps}](img83.png) |