|
Iterazioni nel piano Complesso
Consideriamo adesso il caso complesso (nel senso dei numeri!): il procedimento è come il precedente: si tratta di assegnare una legge iterativa, e vedere per quali valori iniziali la successione diverge oppure no.
Nel trattare questo caso, abbiamo una piccola difficoltà in piu rispetto ai numeri reali: noi non possiamo affermare direttamente se un numero complesso è maggiore o minore di un altro, per confronto diretto: quindi, in questo senso non possiamo dire se un numero complesso diverge oppure no. Questo problema si risolve immediatamente associando la misura e il confronto fra due numeri complessi, come confrono fra i loro moduli, cioè la loro distanza dall'origine, che è data da 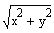 . E' da questo valore che possiamo vedere se un numero complesso diverge oppure no. . E' da questo valore che possiamo vedere se un numero complesso diverge oppure no.
Consideriamo adesso la seguente iterazione:
dove c è una costante complessa. Prendiamo, adesso, una c e una x0 iniziale, ed iteriamola.
|
z0 =0, c =-0.8+0.4i |
| n |
zn |
zn+1 |
|zn+1| |
| 0 |
0 |
-0.8+0.4i |
0.894 |
| 1 |
-0.8+0.4i |
-0.32+0.24i |
0.4 |
| 2 |
-0.32+0.24i |
-0.755+0.554i |
0.936 |
| 3 |
-0.755+0.554i |
-0.536-0.436i |
0.691 |
| 4 |
-0.506-0.436i |
-0.703+0.868i |
1.117 |
| 5 |
-0.703+0.868i |
-1.059-0.82i |
1.339 |
| 6 |
-1.059-0.82i |
-0.35+2.136i |
2.164 |
| 7 |
-0.35+2.136i |
-5.239-1.096i |
5.353 |
| 8 |
-5.239-1.096i |
25.447+11.888i |
28.087 |
| 9 |
25.447+11.888i |
505.448+605.416i |
788.674 |
Si vede facilmente che, dopo un inizio incerto, il modulo dei numeri dell'iterazione tende velocemente ad infinito. Notiamo che ciò vale per un numero il cui modulo iniziale era minore di 1: ciò fa apparire una differenza rispetto al caso dei numeri reali positivi, dove ogni numero con modulo minore di 1 (che corrisponde al numero stesso), convergerebbe a 0.
Consideriamo, adesso, quest'altra iterazione, che ha sempre
z0 = 0, però cambia la costante
|
z0 =0, c =0.25+0.2i |
| n |
zn |
zn+1 |
|zn+1| |
| 0 |
0 |
0.25+0.2i |
0.32 |
| 1 |
0.25+0.2i |
0.273+0.3i |
0.405 |
| 2 |
0.273+0.3i |
0.234+0.364i |
0.432 |
| 3 |
0.234+0.364i |
0.173+0.37i |
0.409 |
| 4 |
0.173+0.37i |
0.143+0.328i |
0.358 |
| 5 |
0.143+0.328i |
0.163+0.294i |
0.336 |
| 6 |
0.163+0.294i |
0.19+0.296i |
0.352 |
| 7 |
0.19+0.296i |
0.199+0.313i |
0.37 |
| 8 |
0.199+0.313i |
0.185+0.313i |
0.363 |
| 9 |
0.185+0.313i |
0.186+0.313i |
0.366 |
Potete notare come l'iterazione non converga ad infinito, ma tenda ad un numero finito, l'attrattore, che fra l'altro non è nè 1, nè tantomeno infinito, ma un numero finito diverso da 0 (lo zero complesso, ma è un particolare secondario).
Questo ci basta per capire come si formano gli insiemi di Mandelbrot e di Julia, dato che si basano su questo principio, e sulla medesima formula iterativa (mica l'ho presa a caso!).
|
|
|

![]()

![]()