Home | Perchè la crittografia | Crittografia a chiave segreta | Crittografia a chiave pubblica | Numeri primi | Aritmetica modulare

Ad ogni utente  del sistema RSA  viene assegnata , tramite un ente che ne garantisce l'autenticità,una coppia di interi positivi, (n, e), consultabile on-line in un database pubblico.
Il primo intero n, detto modulo ,rappresenta il prodotto di due numeri primi distinti, p, q che devono essere grandi e tenuti segreti ; il secondo numero e ,detto esponente pubblico, deve essere scelto dall'utente in modo tale che (e, p -1) =1 e (e, q -1) =1

 Osservazione:

•  la coppia (n, e) e di dominio pubblico, ossia un qualunque utente che lo desideri può consultarla, mentre non è di dominio pubblico la fattorizzazione di n.

 Si ipotizzi che un utente A debba inviare un messaggio M ad un altro utente B consultando il database  ufficiale. L'utente A controlla innanzitutto la coppia di numeri relativa all'utente B, cioè la coppia (n_B, e_B). Se il messaggio M da inviare è maggiore del numero n_B, allora l'utente A spezzerà M in vari blocchi (messaggi unitari) in modo che risultino minori di n_B. In definitiva si può supporre che il messaggio M soddisfi le seguenti due condizioni:

M < n_B,    (M, n_B) = 1.

Per codificare il messaggio M da inviare al destinatario l'utente A, poi, eleva M alla potenza e_B e poi la riduce modulo n_B ossia:

M′ = 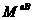 (mod n_B).

Osservazioni:

1) L'utente B pubblica la sua coppia (n_B, e_B), ma tiene per sé la chiave segreta d_B:

1 < d _b< φ(n_B) = (p_B - 1) (q_B - 1),

che è soluzione della congruenza :        e_B d_B  (mod φ(n_B))

dove φ è la funzione di Eulero.

2) Il destinatario può decifrare il messaggio M perchè è l' unico che è in possesso della fattorizzazione di n_B(che è equivalente  alla funzione di Eulero).

3)Il problema della ricerca di due numeri primi grandi ,in modo da produrre n ,si risolve

• generando , a caso, un numero m dispari dell'ordine di grandezza voluto.

• sottoponendo m a un test di primalità.

• considerando l'intero m+2 ,se m non supera il test

• effettuando  al massimo un numero di tentativi, pari a ln(m), in base al Teorema dei Numeri Primi

Punti di forza
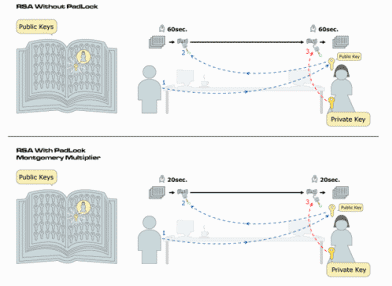
La sicurezza di questo sistema risiede nel fatto che

• non vi è scambio di chiavi tra gli utenti

• dato l'elevato ordine di grandezza,10³⁰⁰ , dei numeri primi  e delle chiavi , 1024 o 2048 bit,attualmente utilizzato, la fattorizzazione ,anche utilizzando i più sofisticati algoritmi e i calcolatori più veloci,  richiede tempi proibitivi

Osservazioni
Il sistema RSA viene utilizzato per:

• votazioni elettroniche;

• firme digitali;

• protocolli per il recupero di informazioni(privacy preserving information retrivial)
   

 Applicazione con Derive

Applicazioni con Excel

Home | Su | Sistema RSA | Crittografia quantistica | Firma digitale