Lezione 23

*Il quadripotenziale elettromagnetico*

di Michele Moroni

Abbiamo dimostato nella lezione precedente che è sempre possibile trovare un campo vettoriale A che soddisfi la relazione:

Possiamo quindi pensare di sostituire questa relazione all'interno della terza equazione di Maxwell

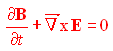
ricavando

dato che le derivate spaziali commutano con la derivata temporale la precedente equazione può essere riscritta come:

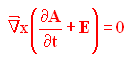
ma il teorema 1 della lezione precedente ci conferma che in questo caso deve esistere un campo scalare V che soddisfa la relazione

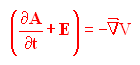(1)

(il segno meno è stato estratto dal campo scalare per motivi che saranno chiari in seguito)

Il campo V che soddisfa questa proprietà è chiamato POTENZIALE SCALARE ELETTRICO

Di solito si preferisce scrivere la relazione (1) come

Risulta evidente che anche il potenziale scalare, come il potenziale vettore, non è univocamente definito; infatti una qualsiasi funzione
V'=V+ cost soddisfa altrettanto bene la relazione precedente.

Abbiamo quindi visto che, per un qualsiasi campo elettromagnetico nello spazio esistono due funzioni (non univocamente definite) tali che siano verificate le seguenti relazioni

Una prima considerazione interessante è basata sul fatto che fissato il campo elettrico e magnetico le funzioni A e V non sono univocamente definite. Infatti le espressioni dei campi rimangono invariate se ad A e V si sostituiscono le relazioni.

e Y è una funzione qualsiasi

Possiamo quindi inserire due qualsiasi soluzioni A e V all'interno delle equazioni 2 è sostituirle all'interno della prima e della quarta equazione di Maxwell, ottenendo rispettivamente

Tenendo conto che la (5b) può essere scritta come

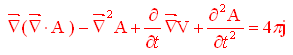
da cui, semplificando...

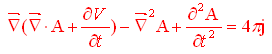
o, se si preferisce

Allo stesso modo possiamo riscrivere la prima equazione di Maxwell come

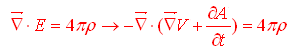
e quindi

Trovare una soluzione generale del sistema costituito dalle equazioni 6 e 7 sfortunatamente non è una cosa facile.Forse pero' possiamo aggirare il problema....

Una prima considerazione possibile nasce osservando che se A e V sono due soluzioni anche A' e V' date dalle relazioni 4 sono soluzioni particolari (come è facile dimostrare per sostituzione). Quindi per una determinata disposizione di carica/corrente elettrica esistono infinite soluzioni A e V che forniscono lo stesso campo elettromagnetico. Noi vogliamo trovare almeno una coppia A,V, non tutte quelle possibili... a questo scopo possiamo quindi imporre delle condizioni al contorno.

Una condizione al contorno piuttosto interessante è data dall'imposizione della relazione

Imponendo che i campi A e B soddisfino questa condizione il sistema fornito dalle 6 e 7 si semplifica in

Trovare una soluzione generale di questa equazione per perticolari distribuzioni di carica/corrente è molto più semplice che trovarla senza imporre la condizione 8. Una volta trovata questa soluzione deve essere nostra cura verificare che soddisfa contemporaneamente la 6, 7 e 8.

Anche le relazioni 9 possono essere scritte in maniera molto elegante con il formalismo proprio della relatività. Infatti introducendo l'operatore (si veda lezione 17) si può osservare che

(Operatore Dalambertiano)

E quindi le relazioni 9 si scrivono come

(Equazioni di Maxwell in forma potenziale)

La bellezza di queste relazioni ci apre nuove affascinanti porte e la prima è basata sul fatto che il D'alambertiano è un invariante lorentziano, infatti

Da questa e dalle relazioni appena introdotte si deduce quindi che V si trsaforma come la densità di carica r, mentre A si trasforma come la densità di corrente J. Ma r e J si trasformano come le componenti di un quadrivettore e quindi anche V e A si devono trasformare in questo modo; conseguentemente

V e A sono le componenti di un quadrivettore [V, A] chiamato QUADRIVETTORE POTENZIALE ELETTROMAGNETICO

Un'altra affascinate porta si basa sul fatto che le equazioni (5) e (6) nel vuoto (r e J nulle) sono equazioni d'onda, e descrivono una propagazione ondulatoria che si muove a velocità c. Ma questa è la velocità di propagazione delle particelle senza massa, e quindi risulta spontaneo associare particelle senza massa ad onde di potenziale... ma di questo parleremo abbondantemente in seguito quindi limitate la vostra curiosità ancora per qualche lezione ;-)

Indice Lezioni - Lezione Precedente - Lezione Seguente