Lezione 17
*Il gradiente relativistico*
Consideriamo una unoforma f che associa ad ogni quadrivettore V uno scalare f, ovvero f=f(V).
Vediamo cosa succede cambiando sistema di riferimento.
Se indichiamo con fi le componenti dell'unoforma, in seguito alla trasformazione di coordinate si ottiene:
Tenendo in considerezione la proprietà di linearità si può quindi scrivere:
Abbiamo quindi dimostrato che
l'output di una unoforma è invariante lorentziano
___________________________
Consideriamo ora lo spazio-tempo e due eventi A e B separati da una distanza infinitesima. Secondo un osservatore inerziale O i due eventi hanno coordinate
A=
, B=
In questi punti dello spaziotempo due rivelatori misurano un campo scalare f e, successivamente comunicano ad O i valori misurati.
Ammettiamo ora che un altro osservatore O' si muova rispetto ad O con velocità v, e che i rivelatori comunichino i valori misurati di f anche a quest'osservatore. Secondo O' chiaramente le misurazioni sono state fatte nei punti
A'=
,
B'=
L'osservatore O misura un intervallo tra le due misurazioni dato da
L'osservatore O' invece misura un intervallo
Chiaramente la differeza tra le due misurazioni del campo scalare df è indipendente dall'osservatore
E' immediato dimostrare che la legge di trasformazione tra dl e dl' è
o, se si preferisce,
(1)
Ovviamente devono essere verificate le relazioni
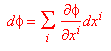(2)
(3)
Combinando la (2) e la (1) (dopo un cambio di variabile muta) si ottiene
Da cui, per confronto con la (2)
Possiamo quindi osservare che le componenti del vettore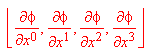
si
trasformano come componenti di un tensore di tipo 0/1.
E' quindi conveniente utilizzare la seguente simbologia
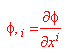
la quale mette ben in evidenza la legge di trasformazione, che viene riscritta come
Inoltre usualmente si utilizza il simbolo
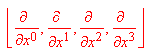
f=
f=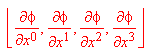
è chiamato TENSORE GRADIENTE
Indice Lezioni - Lezione Precedente - Lezione Seguente