Lezione 12b

*Relatività e campo magnetico*

di Michele Moroni

Consideriamo un filo conduttore molto lungo e molto sottile, (per comodità rivolto nella direzione delle x). Quando non è applicata una differenza di potenziale la velocità media degli elettroni liberi è nulla, così come la densità di carica totale ()

Quando ai capi del filo viene applicata una differenza di potenziale gli elettroni liberi cominciano a muoversi rispetto agli ioni positivi con una velocità media v_d (velocità di drift) generando una corrente di densità j = j_-=(j_-)_x

Consideriamo ora l'osservatore O' che si muove lungo la direzione x con velocità v.

In accordo con quanto ricavato nella lezione precedente possiamo scrivere:

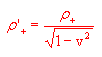
La densità totale di carica vista dall'osservatore O' è quindi

(1)

conseguente l'osservatore O' vede nel filo una densità di carica totale direttamente proporzionale alla densità di corrente.

_________________

Calcoliamo ora il campo elettrico che l'osservatore O' misura

Per effettuare questo calcolo risulta molto comodo utilizzare il teorema di Gauss e sfuttare le caratteristiche di simmetria del sistema.Se il filo è molto lungo il sistema può essere tranquillamente considerato a simmetria cilindrica. possiamo quindi utilizzare un sistema di coordinate cilindriche (r,q,z) e di rispettivi versori (i_r, i_q, i_z)

Considerare quindi la superficie cilindrica su cui si muove l'osservatore O' , avente per asse il filo conduttore e raggio r (pari alla distanza dell'osservatore dal filo)

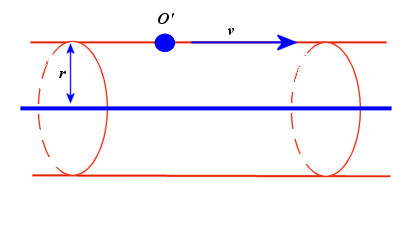
Per le caratteristiche di simmetria del sistema il campo elettrico deve essere per forza radiale. Il teorema di Gauss afferma che.

q' è la carica contenuta nell'elemento di filo di lunghezza l mentre f_E' è il flusso di campo elettrico attraverso la superficie del cilindro di lunghezza l e di raggio r

Essendo il campo elettrico radiale la precedente relazione si riduce a:

E' 2prl = 4pr'ls

dove r' è la densità di carica all'interno del filo (data dall'espressione 1) e s la sezione retta del filo.

Semplificando la precedente relazione si ricava

Sostituendo la relazione (1) e otteniamo che il campo elettrico visto dall'osservatore è dato da:

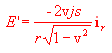
Ma il prodotto js è la corrente che fluisce nel filo; quindi

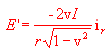
Possiamo immediatamente osservare che il campo elettrico visto dall'osservatore è rivolto radialmente verso il filo quando velocità e corrente hanno la stessa direzione. Se invece velocità e corrente hanno direzione opposta il campo elettrico è rivolto radialmente in direzione contraria al filo.

Quindi una carica puntiforme q che si muova parallelamente ad un filo il cui fluisce una corrente I subisce una forza F' pari a:

(2)

In questo caso è quindi possibile definire un vettore B chiamato CAMPO MAGNETICO definito come:

(3)

tenendo in considerazione che v = v_z e che i_zx i_f= -i_r la relazione (2) può essere scritta semplicemente come:

(4)
(forza di Lorentz)

dove v in questo caso è la componente spaziale del quadrivettore velocità.

La precedente relazione, ricavata per un filo rettilineo, è generalizzabile al caso sia presente una distribuzione di correnti elettriche qualsiasi, nel senso che è sempre possibile definire un campo B che soddisfa la precedente proprietà.

Possiamo notare che la relazione (3) è esattamente l'espressione della legge di Biot e Savart, ricavata classicamente (a meno di una costante moltiplicativa data dal sistema di misurazione)

___________________

Ammettiamo ora che l'osservatore si muova all'interno del filo dove fluisce la corrente (per il momento non ci importa come ci riesce), ad una distanza r<R dall'asse; ci chiediamo quindi quali sono le forze che esso risente.

La densità di carica vista dall'osservatore è ancora chiaramente data dalla relazione (1)

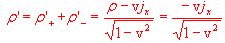
Possiamo ancora utilizzare il teorema di Gauss ricavando, in maniera perfettamente analoga a quella che abbiamo già seguito

E' 2prl = 4pr'ls

dove questa volta s è la superficie del cilindro di raggio r, interno al filo (il teorema di gauss, fra le altre cose, dice anche che le cariche esterne alla superficie non contribuiscono al flusso). Possiamo quindi in questo caso scrivere:

da cui

Per preservare la relazione (4) possiamo definire il campo magnetico all'interno del filo come

B' = 2prj_xi_f

Si noti come il campo magnetico all'interno del cavo si raccorda perfettamente con quello esterno!

Indice Lezioni - Lezione Precedente - Lezione Seguente