Lezione 4

*La dilatazione del tempo e la contrazione delle lunghezze*

di Michele Moroni

Versione 2.0, Gennaio 2004

Consideriamo un sistema di riferimento O' in moto con velocità v rispetto ad un sistema O. Ammettiamo che nello spazio-tempo accadano due eventi che in O' hanno coordinate [t'₁, x'₀, y'₀, z'₀] e [t'₂, x'_0, y'₀, z'₀] (ovvero nella stessa posizione ma separati da un intervallo di tempo Dt'=t'₂-t'₁ ).

Vogliamo trovere le coordinate di questi eventi nel sistema di riferimento O. Applichiamo quindi la trasformazione di Lorentz

Non si perde di generalità ammettendo che la componente spaziale di v sia diretta come l'asse delle x; quindi la trasformazione si scrive

(1)

Quale sarà la trasformazione che permette di passare dal sistema di riferimento O' al sistema O?

Il sistema di riferimento O si muove rispetto ad O' con velocità -v, quindi non è sorprendente il fatto che la matrice di trasformazione si ottenga sostituendo v con -v . In una delle prossime lezioni dimostreremo questa affermazione in termini matematici, per ora basti sapere che il nostro "istinto fisico" non ha fallito ;-)

Risulta quindi

(2)

Da cui si ricava immediatamente

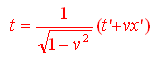
e quindi

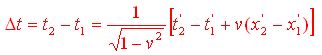
Sapendo che

x'₂=x'₁=x'₀

ovviamente la precedente relazione si riduce a:

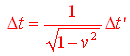
dato che Dt>Dt' l'osservatore O registra un intervallo di tempo tra i due eventi maggiore di quello registrato dall'osservatore O'. Questo fenomeno è conosciuto come DILATAZIONE DEL TEMPO.

Consideriamo un oggetto nello spazio situato sull'asse delle ascisse e in movimento con velocità v. In un generico istante w₀ nello spazio-tempo le sue estremità hanno coordinate A=[w₀,x₁,y₀,z₀] e B=[w₀,x₂,y₀,z₀]. La lunghezza dell'oggetto nel sistema di riferimento O è quindi data da Dx = x₂-x₁

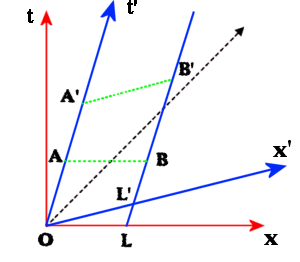
Nel sistema di riferimento O', solidale all'oggetto, la lunghezza viene misurata rilevando contemporaneamente la posizione delle due estremità. Ma la linea di contemporaneità è parallela all'asse x', quindi la distanza viene misurata rilevando la posizione dei punti generici A' e B' nel sistema di riferimento O

Essendo la lunghezza dell'oggetto invariante rispetto all'istante in cui si considera (come è evidente dal grafico) non si perde di generalità misurandola quando l'estremità A si trova nell'origine O (in entrambi i sistemi di riferimento)

La lunghezza misurata dall' osservatore O è: Dl=L-O

All'istante t' = 0 l'estremità B, secondo il sistema O' si trova nel punto L'. Le coordinate di L' secondo il sistema di riferimento O si ottengono dal sistema

x= Dl + vt

x = t/v

(quest'ultima è l'equazione asse x' in O)

Risolvendo il sistema otteniamo che la posizione del punto L'(O) è

Per passare al sistema di coordinate O' si applica la (1) al vettore [t,x] appena definito, ricavando

w'=0 (come è ovvio per costruzione)

e

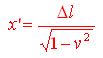
Dato che l'estremità A nel sistema di riferimento O' ha coordinate (0,0) la lunghezza dell'oggetto in O' è proprio

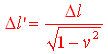
e quindi

ovvero

quando un oggetto si muove con velocità v rispetto ad un osservatore la sua lunghezza risulta contratta di un fattore (contrazione delle lunghezze)

Indice Lezioni - Lezione Precedente - Lezione Seguente