Lezione 12
*Quadriaccelerazione, quadriforza e dinamica relativistica*
La quadriaccelerazione di una particella è un quadrivettore definito come la derivata della quadrivelocità rispetto al tempo proprio:
Sviluppando la precedente relazione:
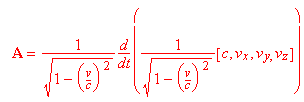
da cui, ovviamente...
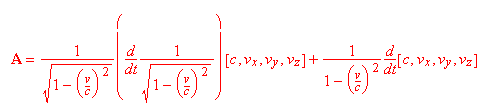
e quindi
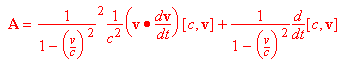
la precedente relazione è spesso scritta in forma compatta come
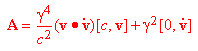
Espressione standard della quadriaccelerazione
Nel caso di basse velocità (v<<c) il fattore g tende ovviamente a 1, e quindi la quadriaccelerazione si riduce a:
Quindi, come dovevamo aspettarci, al limite per basse velocità la parte spaziale della quadriaccelerazione tende all'accelerazione classica.
|
Teorema: La quadriaccelerazione è sempre ortogonale alla quadrivelocità Dimostrazione: La quadrivelocità soddisfa la relazione U·U=-c2. Derivando entrambi i membri rispetto al tempo proprio otteniamo:
la quale basta a dimostrare il nostro teorema. |
Definiamo infine la quadriforza come il quadrivettore
F=m0A
Cnsideriamo ora un sistema isolato di n particelle. In questo caso postuliamo che, fissato un sistema di riferimento, sia verificata la relazione
SiPi=costante
(Conservazione del quadrimpulso totale)
dove i identifica la singola particella e Pi il suo quadrimpulso. Ovviamente la conservazione della componente temporale si riduce alla conservazione dell'energia mentre la conservazione della componente spaziale si riduce alla conservazione della quantità di moto.
L'impulso totale è una grandezza Lorentz invariante (il suo modulo quadro è costante in ogni sistema di riferimento)
In generale risulta comodo introdurre il centro di massa come quel sistema di riferimento per cui vale la relazione:
SiPi = [Etot/c, 0, 0, 0]
Indice Lezioni - Lezione Precedente - Lezione Seguente
