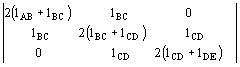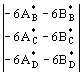La risoluzione della trave continua

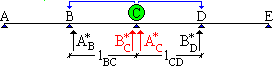
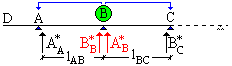
La risoluzione della trave continua.
La trave in figura ha cinque appoggi ed è tre volte iperstatica.		La determinazione del grado di iperstaticità. Per ottenere il numero n di incognite iperstatiche si sottraggono al numero di appoggi m i due appoggi strettamente necessari a garantire l'isostaticità della struttura: n = m-2.
La trave continua è stata separata in più travi isostatiche aggiungendo i momenti che , in relazione all'iniziale continuità, i vari elementii si scambiano. I momenti sono ipotizzati in senso orario per l'estremità sinistra della campata e in senso antiorario per quella destra; in tal modo essi risultano positivi in quanto tendono le fibre inferiori della struttura.		Le incognite iperstatiche. Si assumono quali incognite iperstatiche gli n momenti sugli appoggi intermedi; per ognuno di tali appoggi si scrive un'equazione dei tre momenti, ottenendo così un sistema lineare di n equazioni in n incognite.
Ogni equazione, scritta per un appoggio intermedio, coinvolge il momento su tale appoggio e gli altri due momenti sugli appoggi vicini.		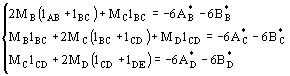	Nella prima equazione figurano solo due dei tre momenti essendo nullo il momento M_A nell'estremo appoggiato della trave. Analogamente, nell'ultima equazione non è presente il momento M_E. Il calcolo dei valori delle reazioni della trave ausiliaria 6A* e 6B*, i termini noti dell'equazione, è facilitato dall'uso di appositi formulari.
La matrice dei coefficienti e il vettore dei termini noti da introdurre nel foglio elettronico. La matrice dei coefficienti contiene solo indicazioni sulla geometria della trave, essendo basata sulle luci delle campate. In assenza dell'incognita nella singola equazione, il coefficiente è pari a zero.			Se il numero delle equazioni è elevato è consigliabile l'uso di un foglio elettronico per la soluzione del sistema.
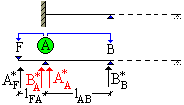
Vincolo d'estremità incastrato. L'incastro in A è trasformato in un doppio appoggio fittizio, introducendo la campata AF, scarica e di luce pari a zero.	Vincoli d'estremità diversi dall'appoggio semplice. Se la trave è incastrata a una o a entrambe le estremità, si trasforma l'incastro in un doppio appoggio fittizio. La nuova campata introdotta ha luce nulla ed è scarica. L'equazione dei tre momenti, scritta nella sezione d'incastro A diventa: Essendo nulli l'equazione si semplifica nella
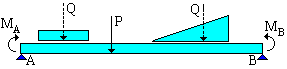
Estremo a sbalzo. Le caratteristiche di sollecitazione del tratto a sbalzo DA sono calcolabili prima ancora di iniziare il calcolo delle incognite iperstatiche. In particolare il momento M_A può essere trasportato a destra del segno di uguale, nell'equazione dei tre momenti, essendo un termine noto e non un'incognita.	Se la trave ha uno o entrambi gli estremi a sbalzo, come nella trave a lato, l'equazione dei tre momenti diventa essendo calcolabile, e quindi noto a priori, il momento M_A.
Il completamento del calcolo. La trave continua, dopo il calcolo dei momenti incogniti iperstatici, può essere trattata come una serie di travi semplicemente appoggiate del tipo di quella in figura.	Il completamento del calcolo. Determinati i momenti incogniti sugli appoggi intermedi, si procede al calcolo delle sollecitazioni. Il procedimento consiste nel tracciamento dei diagrammi relativi alle singole campate, semplicemente appoggiate e caratterizzate dalla presenza dei momenti in corrispondenza degli estremi. Per il calcolo del taglio nella sezione immediatamente a destra del primo appoggio ci si può utilmente avvalere di appositi formulari. Le reazioni vincolari possono essere calcolate dopo il tracciamento del diagramma del taglio mediante la formula essendo, in generale,