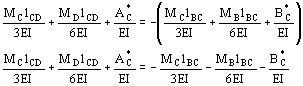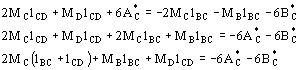L'equazione di Clapeyron

L'equazione di Clapeyron.
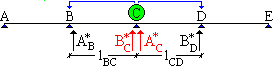
La trave in figura ha cinque appoggi ed è tre volte iperstatica.		Il grado di iperstaticità della trave continua. Una trave isostatica semplicemente appoggiata è isostatica quando risulta vincolata solo con un carrello e una cerniera. Ogni ulteriore carrello aggiunto alla struttura comporta un aumento del grado di iperstaticità. Più in generale, se m sono gli appoggi della trave il grado di iperstaticità sarà pari a n = m-2.
Separando i diversi elementi della trave occorre aggiungere i momenti interni che essi si scambiano. I momenti sono ipotizzati in senso orario per l'estremità sinistra della campata e in senso antiorario per quella destra. Entrambi i momenti risultano positivi in quanto tendono le fibre inferiori della struttura.		La determinazione delle incognite iperstatiche. In presenza di n appoggi sovrabbondanti si assumono quali incognite iperstatiche gli n momenti sugli appoggi intermedi, per la cui determinazione occorre risolvere un sistema di n equazioni. Se il numero delle equazioni è elevato è consigliabile l'uso di un foglio elettronico per la soluzione del sistema.
Per la continuità della linea elestica deve risultare a_C = b_C
L'equazione dei tre momenti. Per la scrittura delle n equazioni di iperstaticità si fa uso del metodo delle rotazioni. L'espressione della linea elastica è una funzione continua: la tangente a tale linea nel punto C in figura deve essere la stessa per i due tratti BC e CD. In altri termini l'angolo b_C deve risultare uguale all'angolo a_C. La rotazione a_C, applicando il principio di sovrapposizione degli effetti, è il risultato di tre azioni: il momento M_C, il momento M_D e i carichi esterni agenti sulla campata BC. Se con si indica la reazione dell'appoggio sinistro della trave ausiliaria corrispondente alla trave BC caricata con le sole azioni esterne, si ottiene Analogamente per la rotazione b_C si ha La rotazione b_C è negativa, in accordo con le convenzioni di segno. Nelle due espressioni precedenti il modulo elastico E e il momento di inerzia baricentrico I della sezione sono stati supposti uguali per le due campate. Posto a_C = b_C si ha Razionalizzando per 6EI si ottiene Quest'ultima equazione prende il nome di equazione dei tre momenti o equazione di Clapeyron (Benoit Paul Emile, 1799-1864) che per primo la propose.
L'equazione di Clapeyron, scritta per l'appoggio C, coinvolge i due appoggi vicini B e D.	Nel primo termine vi figurano: il doppio del momento sull'appoggio centrale moltiplicato per la somma delle due luci laterali; il momento dell'appoggio posto a sinistra per la luce di sinistra; il momento dell'appoggio di destra per la luce di destra. Nel secondo termine si trovano, moltiplicate per sei: la reazione destra della trave ausiliaria di sinistra; la reazione sinistra della trave ausiliaria di destra. La scrittura dell'equazione è facilitata dalla presenza di numerose soluzioni delle reazioni della trave ausiliaria, reperibili nei formulari.