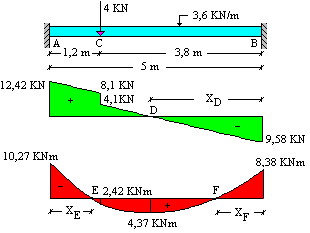
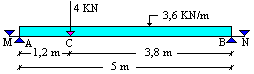
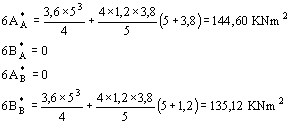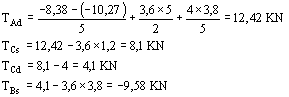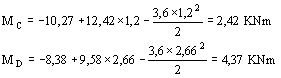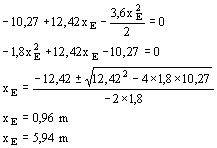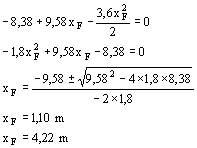Trave iperstatica a una campata. Esempio di calcolo. Problema. Tracciare i diagrammi delle sollecitazioni della trave in figura. |
|
|
|
 I due incastri sono stati trasformati in due coppie di appoggi fittizi. Le campate MA e BN sono scariche ed hanno luce nulla; risultano, pertanto, nulle le reazioni delle travi ausiliarie ad esse associate. |
Trasformati gli incastri in un doppio appoggio ravvicinato, la trave presenta 4-2=2
gradi di iperstaticità. Si assumono quali incognite iperstatiche i due momenti MA ed MB. Le reazioni delle travi ausiliarie corrispondenti alle travi reali MA, AB e BN valgono:
|
| Scrivendo l'equazione dei tre momenti nei punti A
e B si ottiene rispettivamente:
Risolvendo il sistema con il metodo di sostituzione o attraverso un foglio elettronico si ricavano i valori: MA = -10,27 KNm MB = -8,38 KNm Con l'ausilio di un formulario si può ricavare rapidamente il valore del taglio nella sezione immediatamente a destra di A
La variazione del taglio è lineare e la distanza xD vale:
La variazione del momento è parabolica; si ha:
Posto ME = 0 si ottiene
La seconda soluzione è da scartare perché il punto E deve risultare compreso tra A e C. Posto MF = 0, analogamente si ha:
La seconda soluzione è da scartare perché il punto F deve risultare compreso tra B e C. |
|