Un transistor è assimilabile a un carico non lineare, quindi ci troviamo in condizioni di funzionamento non sinusoidale.
Nel caso generale la potenza attiva media è definita come:
dove ![]() è l'intervallo di osservazione o, per segnali periodici,
il periodo.
è l'intervallo di osservazione o, per segnali periodici,
il periodo.
Avendo a disposizione i campioni della tensione e della corrente acquisiti dall'oscilloscopio, usiamo il metodo di integrazione discreta:
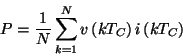
dove ![]() è il periodo di campionamento.
è il periodo di campionamento.
Un carico non lineare introdurrà distorsione, quindi tensione e corrente saranno non sinusoidali e conterranno armoniche.
Se tensione e corrente sono sinusoidali possiamo scrivere:
dove ![]() e
e ![]() sono i valori efficaci di tensione e corrente
e
sono i valori efficaci di tensione e corrente
e ![]() è l'angolo di sfasamento tra le due sinusoidi.
è l'angolo di sfasamento tra le due sinusoidi.
Se tensione e corrente sono non sinusoidali e periodici di periodo
![]() , possiamo scrivere [1]:
, possiamo scrivere [1]:
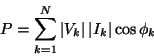
dove ![]() e
e ![]() sono i coefficienti della DFT e
sono i coefficienti della DFT e ![]() è l'angolo di sfasamento tra
è l'angolo di sfasamento tra ![]() e
e ![]() .
.
La potenza reattiva e la potenza apparente non sono basate su un singolo e ben definito fenomeno fisico così come la potenza attiva, ma sono quantità definite convenzionalmente, utili in regime sinusoidale o quasi sinusoidale.
Per corrente e tensione sinusoidali la potenza reattiva è definita come:
La potenza apparente è definita come:
In regime non sinusoidale esiste un accordo generale sulla formula [1]:
quindi per segnali periodici non sinusoidali si ha:
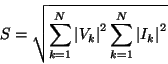
Esistono diverse definizioni di potenza reattiva in regime non sinusoidale. Esamineremo e simuleremo due di queste definizioni, una proposta da C. Budeanu [2], l'altra proposta da un gruppo di lavoro dell'IEEE [3].