Media ponderata
prerequisiti
Si è studiato che le grandezze derivate come per esempio la densità "accumulano" gli errori
derivanti dalle singole misure, è quindi spesso necessario applicare delle tecniche che permettano
di ridurre gli errori. Si può operare con strumenti di più alta precisione, si può ripetere la misura
con un altro operatore, o si possono effettuare più misure così da mediare tra più valori.
Se i risultati ottenuti hanno diversi valori dell'errore non si può operare con una semplice media
tra più valori di misura
m1, m2, m3, m4:
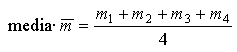 con con 
o, meglio ancora, applicando la deviazione standard
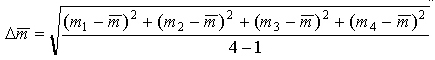
ma è meglio operare con una media ponderata.

con errore assoluto associato
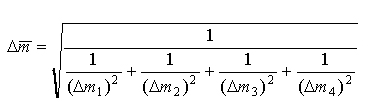
Per esempio trovate quattro densità per la glicerina C3H8O3
d1 ±Δd1, d2 ±Δ
d2, d3 ±Δd3, d4 ±Δd4, per trovare
la media ponderata e il relativo errore assoluto si applicano, le ultime formule:
| densità in g/cm3 | Δd | (Δd)2 | d/(Δd)2 | 1/(Δd)2 |
| prova 1 | 1,10 | ±0,024 | 0,000576 | 1909,722 | 1736,111 |
| prova 2 | 1,18 | ±0,05 | 0,0025 | 472,000 | 400,000 |
| prova 3 | 1,16 | ±0,13 | 0,0169 | 68,639 | 59,172 |
| prova 4 | 1,07 | ±0,12 | 0,0144 | 74,306 | 69,444 |
| calcoli | | | somme | 2524,667 | 2264,727 |
da cui risulta il valore finale per la glicerina di 1,11 ± 0,02 g/cm3.
Il valore reale a 20° risulta 1,26362 e noi essendo fuori dall'intorno di valori esatto possiamo forse pensare che la glicerina di laboratorio
fosse un po' annacquata o che ci sia stato un errore nelle misure svolte in laboratorio.
Per esempio trovate quattro densità per il mercurio Hg
d1 ±Δd1, d2 ±Δ
d2, d3 ±Δd3, d4 ±Δd4, per trovare
la media ponderata e il relativo errore assoluto si applicano, le ultime formule:
| densità in g/cm3 | Δd | (Δd)2 | d/(Δd)2 | 1/(Δd)2 |
| prova 1 | 12,505 | ±1,5681 | 2,4590 | 5.0853 | 0,4067 |
| prova 2 | 13,181 | ±0,7344 | 0,5394 | 24,4362 | 1,8539 |
| prova 3 | 13,385 | ±1,2766 | 1,6298 | 8,2124 | 0,6136 |
| prova 4 | 13,460 | ±1,0573 | 1,1178 | 12,0415 | 0,8946 |
| calcoli | | | somme | 49,7754 | 3,7687 |
da cui risulta il valore finale per il mercurio di 13,2 ± 0,5 g/cm3.
Il valore reale a 25° risulta 13,534 quindi all'interno del valore sperimentale da noi trovato in laboratorio.
La prova è quindi riuscita con successo.
Bibliografia
Si ringraziano idee e suggerimenti del collega prof. Angelini Andrea.
|