| |
Il principio di indeterminazione
Finora non abbiamo mai messo in dubbio che si possa misurare qualsiasi grandezza fisica
con il grado di accuratezza voluto, a patto di possedere uno strumento
sufficientemente preciso: nella fisica classica si è sempre supposto che, entro
i limiti degli errori sperimentali, la misura di una grandezza può essere
eseguita con precisione sempre più rigorosa, a condizione di utilizzare un
dispositivo sempre più sofisticato ed una tecnica sempre più perfezionata. La
meccanica ondulatoria ci mostra invece che anche in esperimenti « ideali », cioè
in cui si ipotizza l'uso di strumenti perfetti, vi sono limiti alla precisione
con cui una misura può essere effettuata, perché misurare significa sempre perturbare il sistema e quindi anche le grandezze che lo
caratterizzano.
La precisione dipende dallo strumento di misura
Prendiamo in esame le operazioni necessarie per misurare la velocità e la posizione di
un'automobile che si muove lentamente su una strada. Possiamo rilevare la
posizione dell'estremità anteriore dell'automobile in un dato istante tracciando
un segno per terra; contemporaneamente facciamo partire un contasecondi, che
verrà fermato nell'istante in cui l'estremità anteriore dell'automobile
raggiunge un altro segno prestabilito sul terreno. Possiamo quindi ottenere la
velocità media dividendo la misura della distanza tra i due segni per la misura
del tempo impiegato a percorrerla. In questo modo sappiamo che l'automobile,
nell'istante in cui raggiunge il secondo segno, si trova a una certa distanza
dal punto di partenza e ha viaggiato a una certa velocità media. Considerando
intervalli sempre più piccoli potremmo anche ottenere la velocità istantanea in
ogni punto della traiettoria.
Analizziamo ora in che modo abbiamo ottenuto le informazioni
necessarie. Abbiamo determinato la posizione dell'automobile grazie alla luce
del sole riflessa dalla parte anteriore dell'automobile verso i nostri occhi,
che ci ha permesso di vedere quando l'automobile raggiungeva il segnale sulla
strada. Per determinare la velocità media abbiamo dovuto verificare due volte la
posizione della sua estremità anteriore.
Supponiamo adesso di usare onde radio invece di luce
visibile. Alla frequenza di 1000 kHz, tipica dei segnali radio, corrisponde una
lunghezza d'onda pari a:
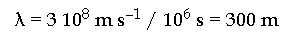
Con radiazioni di questa lunghezza d'onda, molto maggiore
delle dimensioni dell'auto, è impossibile localizzarla con una precisione
qualsiasi, perché l'onda verrebbe riflessa o meglio diffusa dall'automobile in
tutte le direzioni, proprio come farebbe qualsiasi dispositivo di analoghe
dimensioni di cui ci volessimo servire per determinare la direzione dell'onda.
Infatti, per determinare la posizione di un oggetto, si deve usare una
radiazione di lunghezza d'onda vicina o inferiore alle dimensioni dell'oggetto
stesso. Usando onde radar, e cioè con lunghezze d'onda che vanno da 0,1 a 3 cm,
l'incertezza nelle misure sarebbe stata di parecchi centimetri; con la luce
visibile, la cui lunghezza d'onda è minore di 10–6 m, potremmo invece
costruire strumenti così precisi da determinare la posizione dell'automobile con
un'accuratezza di pochi millesimi di millimetro.
Il caso (anomalo) dell'elettrone
Consideriamo ora un elettrone che si muove in un tubo a
vuoto, e cerchiamo di misurarne posizione e velocità. Per fare ciò è necessario
apportare alcuni cambiamenti nei metodi di misura, perché l'elettrone è talmente
piccolo che non è possibile determinarne la posizione usando luce visibile: la
lunghezza d'onda di questa, pur estremamente piccola, è ancora almeno
104 volte più grande del diametro di un atomo.
Per localizzare un elettrone entro una regione di dimensioni
atomiche (circa 10–10 m), si deve usare una radiazione di lunghezza
d'onda confrontabile con le dimensioni atomiche, preferibilmente minore. Ora, un
fotone di lunghezza d'onda così piccola possiede una quantità di moto (h/λ) e
un'energia (hf) molto grandi; dallo studio dell'effetto Compton sappiamo che,
durante l'urto, il fotone trasferisce all'elettrone un forte impulso, con il
risultato che la sua velocità assumerà una direzione nuova, a noi sconosciuta.
Questo è un problema del tutto nuovo che non era neppure immaginabile nella
misura di posizione dell'automobile!
Quindi, dalla direzione del fotone diffuso, possiamo dedurre
la posizione in cui si trovava l'elettrone riuscendo così a « localizzarlo », ma
dobbiamo tener presente che nel corso del processo di misura abbiamo alterato la
velocità dell'elettrone sia in modulo, sia in direzione. In modo più esplicito,
quanto maggiore è la precisione con cui determiniamo la posizione dell'elettrone
usando fotoni di lunghezza d'onda più corta, tanto minore è la precisione con
cui ne conosciamo la velocità. Potremmo tentare di perturbare meno l'elettrone
impiegando fotoni dotati di energia minore, ma poiché la luce esiste sotto forma
di quanti di energia hf, un fotone di energia minore avrà lunghezza d'onda λ più
grande, e quindi ci darà una indeterminazione maggiore nella misura della
posizione dell'elettrone.
Riassumendo: ci troviamo nell'impossibilità di misurare
contemporaneamente la posizione e la velocità di un elettrone con precisione
illimitata.
Questa conclusione è espressa nel principio di indeterminazione che fu stabilito per la prima
volta da Werner Heisenberg. Esso può essere espresso quantitativamente in una
semplice formula. Sappiamo che, se effettuo una misura della posizione di una
particella, il risultato sarà del tipo x ± Δx, dove Δx è l'incertezza nella
posizione; analogamente, la sua quantità di moto p = m v sarà espressa da una
quantità del tipo p ± Δp, dove Δp è l'incertezza nella quantità di moto. Allora
il loro prodotto deve soddisfare la relazione:
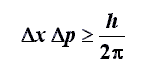
dove h è la costante di Planck. Lo stesso ragionamento vale
anche per l'esperimento dell'automobile, ma le limitazioni non hanno conseguenze
pratiche per un oggetto di massa considerevole. È solo su scala atomica che la
limitazione diventa evidente e importante, come potete vedere negli esempi seguenti.
Una semplice deduzione del principio di Heisenberg
Lo sconvolgente principio di Heisenberg si può ricavare in maniera rigorosa dall'equazione di
Schrödinger per il moto di una particella; un esempio semplice è sufficiente per rendercene conto.
Cimentiamoci nel tentativo di determinare la posizione di un elettrone mediante
un microscopio, come illustrato nella figura seguente:
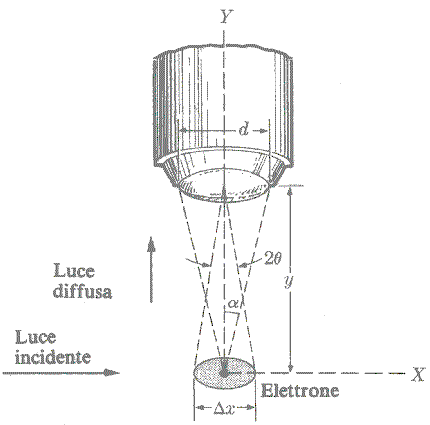
Per osservare l'elettrone, dobbiamo illuminarlo con luce di
una certa lunghezza d'onda λ. La luce che entra nel microscopio è quella diffusa
dall'elettrone sotto osservazione. La quantità di moto dei fotoni diffusi è
pf = h / λ, e per poter entrare nell'obiettivo, i fotoni devono
muoversi entro il cono di angolo α, cosicché la componente X della loro quantità
di moto è affetta da una indeterminazione pari a:
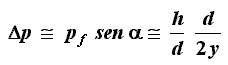
dato che sin α ≈ d/2y. Questa è anche
l'indeterminazione nella componente X della quantità di moto dell'elettrone dopo
la diffusione di luce, dato che nel processo di diffusione viene scambiata
quantità di moto fra elettrone e fotone. D'altra parte, la posizione
dell'elettrone è indeterminata a causa della diffrazione della luce che ha luogo
quando la luce stessa passa attraverso l'obiettivo del
microscopio.
L'indeterminazione nella posizione dell'elettrone è dunque
uguale al diametro del disco centrale nella figura di diffrazione. Tale diametro
è dato da 2y sin θ, con sin θ ≈ λ /d. Quindi:
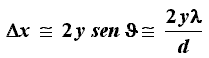
Perciò si ottiene proprio Δx Δp ≈ h. Si osservi come per
migliorare l'accuratezza della nostra determinazione della posizione
dell'elettrone, dovremmo usare radiazione di lunghezza d'onda molto piccola, ciò
che darebbe come risultato un disturbo notevole della quantità di moto.
Inversamente per produrre un disturbo piccolo nella quantità di moto, dovremmo
usare radiazione di lunghezza d'onda molto grande, e questo a sua volta
produrrebbe una notevole indeterminazione nella posizione, per via degli
inevitabili fenomeni di diffrazione.
Quest'esempio mostra chiaramente come il principio di
indeterminazione sia una conseguenza diretta del processo di misura. A livello
atomico, la misura introduce inevitabilmente una perturbazione significativa nel
sistema, a causa dell'interazione fra l'apparato di misura e la grandezza
misurata.
Oltre a quello appena descritto, numerosi sono gli
esperimenti reali o ideali, purché concettualmente possibili, mediante i quali è
possibile controllare la validità del principio di Heisenberg. A questo
proposito, sarà bene sgombrare il campo da un equivoco.
Con l'espressione « concettualmente
possibile » intendiamo un'esperienza, ovvero un dispositivo di misura,
che non sia contraddetto da alcun principio fisico o più in generale da alcuna
incongruenza di natura matematica o fisica, anche se, per difficoltà tecniche,
oggigiorno l'esecuzione non e praticamente realizzabile. Per esempio, non è
concettualmente possibile determinare in modo esatto la lunghezza di una
circonferenza essendo noto il raggio, in quanto pi greco è un numero irrazionale
e trascendente, ne' accelerare un corpo ad una velocità maggiore di quella della
luce nel vuoto, ne' usare una sorgente che possa emettere mezzo fotone,
eccetera. Invece è concettualmente possibile considerare un razzo che si muove a
velocità prossima a quella della luce, una sorgente che emette un solo fotone,
ridurre gli attriti fin quasi a zero, e chi più ne ha, più ne
metta.
La relazione di indeterminazionone tra tempo ed energia
Il principio di Heisenberg sopra scritto equivale in realtà a tre relazioni scalari di
indeterminazione, che si possono scrivere:
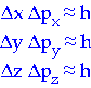
Oltre a queste tre relazioni di indeterminazione fra una
coordinata e la rispettiva componente della quantità di moto di una particella,
si ha anche una relazione di indeterminazione fra tempo ed
energia. Supponiamo difatti di voler misurare non solo l'energia di una
particella ma anche di voler determinare l'istante in cui la particella ha tale
energia: se Δt e ΔE sono le indeterminazioni nei valori di tali grandezze, vale
la relazione: 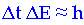
Infatti nella teoria della relatività ristretta il tempo, o meglio la variabile spaziale ct, serve da
quarta coordinata, per cui Δx, Δy e Δz andranno sostituiti con c
Δt. Ma l'energia E divisa per la
velocità della luce c funge a sua volta da quarta componente della quantità di
moto, perché E = m c2 e quindi m c = E/c. Ne segue che a
Δp va sostituita ΔE/c.
Moltiplicando tra di loro c Δt e ΔE/c come se fossero le grandezze coniugate di
una relazione di indeterminazione la velocità della luce si elide ed ottengo
proprio : 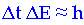
A proposito, due grandezze si dicono canonicamente
coniugate quando la prima descrive un sistema in termini di spazio e di
tempo, mentre la seconda (velocità, energia, momento, ecc...) precisa il suo
stato dinamico. Dunque x e px, t ed E sono canonicamente coniugate
tra di loro. Ebbene, in meccanica quantistica due grandezze
canonicamente coniugate sono sempre legate tra di loro da un principio di
indeterminazione. Ciò significa semplicemente che, anche con metodi di
misura perfezionati all'infinito, la determinazione simultanea di due grandezze
coniugate fra loro è sempre affetta da una certa indeterminazione, regolata dal
principio di Heisenberg. Questo vale quindi anche per <θ ed
L, essendo θ l'angolo di rotazione ed L la corrispondente componente
del momento angolare.
Vivere in un universo quantistico
Vediamo ora due semplicissimi esempi di applicazione del principio di Heisenberg.
Consideriamo anzitutto un'automobile con una massa di
1000 Kg che si muove con la velocità di 10 m s-1, misura questa
affetta da un errore dell'ordine di 0,1 m s-1 (cioè dell'1
%).
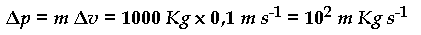
Poiché, secondo il principio di indeterminazione, come minimo il prodotto tra
Δx e Δp deve risultare dell'ordine di h, possiamo ricavare facilmente Δx:
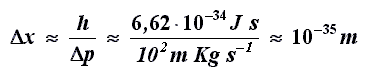
Questa è l'incertezza sulla posizione dell'auto imposta dal principio di Heisenberg.
Poiché un nucleo atomico misura circa 1 Fermi = 10-15 m, se ne
conclude che questa incertezza è mille miliardi di miliardi di volte più piccola
della più piccola misura che la Fisica riesca ad effettuare. Dunque non
incontriamo nessun problema nel determinare la posizione di un'automobile, dato
che una misura così accurata sulle nostre strade non avrebbe alcun senso.
Prendiamo invece in considerazione un elettrone, che ha una
massa di 9 · 10-31 Kg e si muove con una velocità di 2 · 106 m s-1. Se l'incertezza sulla velocità è la stessa di
quella valutata nel caso dell'automobile, cioè l'1 %, ora Δv = 2 104 m s-1.
L'incertezza sulla quantità di moto è allora:
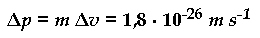
Si ricava allora immediatamente:
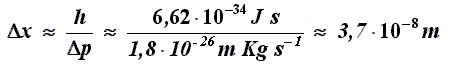
Quest'incertezza è solo apparentemente piccola, poiché un'orbita elettronica ha un ordine di
grandezza di circa 10-10 m. Fatte le debite proporzioni, sarebbe come
se io conoscessi la posizione dell'auto con un'incertezza di un chilometro; ciò
equivarrebbe a dire che io non so dove si trova l'auto, dato che essa misura
solo pochi metri. Dal calcolo precedente ne consegue che io non so dove si trova l'elettrone dentro l'atomo:
l'indeterminazione sulla sua posizione è totale.
La ragione dell'evidente disparità di questi due risultati è molto semplice da
individuare: la costante h di Planck è talmente piccola, che il principio di
Heisenberg risulta del tutto trascurabile su scala umana, per diventare invece
importante su scala atomica. Gli oggetti che capitano sotto i nostri occhi
perciò si comportano effettivamente come predice la Meccanica
Classica.
Sarebbero diverse le cose in un "universo parallelo" nel quale h valesse 100 J s. Nel caso
dell'auto, infatti, il Δx varrebbe proprio un metro, con la conseguenza che io
incontrerei notevoli difficoltà a determinare la posizione della mia auto, e
rischierei di tamponare il veicolo che procede davanti a me perchè la distanza
che mi separa da lui è diventata inferiore a questa fatidica soglia di un metro,
ed io non sono riuscito a valutare correttamente la posizione della mia auto. In
tal caso vivremmo in un vero e proprio universo quantistico, e rischieremmo di
subire noi stessi gli effetti del dualismo onda-particella, finendo per...
diffrangere attraverso la porta di casa nostra!!!
|


