Il peso di un veicolo, in condizioni statiche (assenza di movimento), è distribuito come spiegato nel Capitolo 6. La terza legge di Newton, forza = massa ´ accelerazione, implica che, ogni volta che il veicolo accelera in una direzione, si generano delle forze che si aggiungono a quella di gravità. Ad esempio, quando la macchina atterra dopo un salto, la sua velocità verticale decresce molto rapidamente, in pratica smette piuttosto bruscamente di cadere. La forza aggiuntiva che si esercita sul veicolo è in questo caso pari al prodotto della massa del veicolo per la decelerazione verticale.

Per fare un esempio numerico, si supponga che discesa della macchina sia durata un secondo. Appena prima che impatti la superficie, la sua velocità verticale sarà pari a G ´ 1 secondo = 10 m/s. Supponiamo che la macchina pesi 1 kg = 10 Newton, e le sospensioni richiedano 0,1 secondi per assorbire l'impatto dell'atteraggio. La forza risultante sui pneumatici è quindi pari a 1kg ´ 10m/s / 0.1s = 100N = 10kg. Quindi, nel breve istante dell'atterraggio è come se la macchina pesasse 10 kg anziché 1 kg.

Vi chiederete che importanza abbia. Semplice: il carico sopportato da ciascun pneumatico ne determina la tenuta di strada, e quindi influenza il comportamento della macchina. In effetti potremmo dire che il trasferimento del peso sia l'argomento di per sé più importante nelle competizioni automobilistiche, e anche quello che distingue i bravi piloti da quelli mediocri. E' la capacità di sapere dove si scarica il peso dell'automobile in ogni dato istante, in modo da mantenere i pneumatici al limite delle loro possibilità, che rende veloce un pilota.

Dato che il nostro mondo si estende in 3 dimensioni, anche il trasferimento di peso è un fenomeno tridimensionale (suppongo che in un mondo a 4 dimensioni sarebbe troppo facile fare i furbi). In presenza di movimento verticale, il peso può essere aumentato o sottratto. La dimensione verticale è un po' differente dalle due orizzontali, per la presenza della forza di gravità. La macchina può trovarsi incondizioni di pesare molte volte il suo peso normale (quello che ha procedendo su una strada piana) quando attacca una salita o impatta un'asperità del terreno, come anche di trovarsi in assenza di peso (mentre sta volando in un salto), o di pesare meno del normale (nel tratto discendente di una cunetta). E non si dimentichi la deportanza, che concorre ad aumentare il peso della macchina sui pneumatici. Fortunatamente, nelle altre due dimensioni il peso totale è costante, può solo spostarsi da una parte all'altra, come nelle accelerazioni, quando il peso viene spostato dalle ruote anteriori a quelle posteriori, ma il totale rimane costante. Stessa storia quando si affronta una curva, solo in un'altra dimensione: il peso viene spostato dai pneumatici interni a quelli esterni, ma ancora il totale rimane costante. Per semplicità, d'ora in poi supporremo che la pista sia orizzontale, ignorando il primo caso.

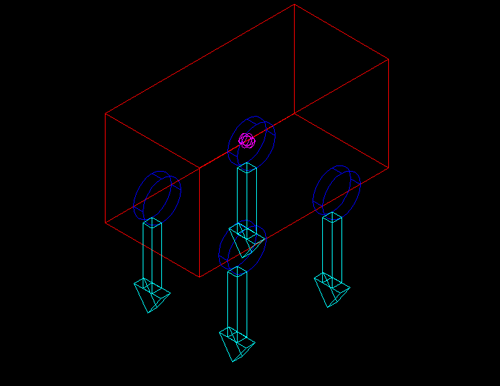
Si consideri il caso seguente: il baricentro (in viola) si trova proprio nel mezzo, e la macchinaprocede a velocità costante (se è ferma la velocità rimane costante a zero), in linea retta e su una superficie perfettamente orizzontale. In questo caso, se il peso totale è pari a W, i pneumatici sopportano tutti lo stesso peso, pari a W/4.

Nota: c'è una piccola incongruenza in questi disegni: le frecce azzurre rappresenano il peso che insiste sui pneumatici. L'incongruenza sta nel fatto che tutte le altre forze sono disegnate applicate alla macchina, mentre queste sono disegnate come se fossero esercitate dalla macchina.

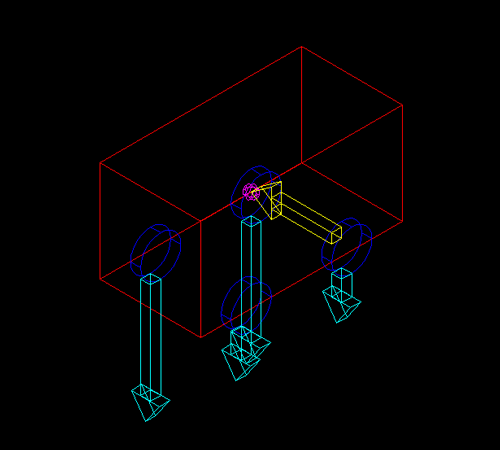
Questa è la medesima macchina mentre affronta una curva. Sta ancora procedendo a velocità costante su una superficie orizzontale, ma ora la direzione di marcia sta cambiando, con un raggio di sterzata costante.

Innanzitutto, nel disegno non sono state rappresentate tutte le forze, per non complicarlo eccessivamente. Su ogni pneumatico agisce una forza orizzontale, e queste quattro forze controbilanciano quella disegnata in giallo. Sono sostanzialmente le forze d'attrito del pneumatico col terreno. Anche il vettore dlla forza peso non è disegnato, anche se è applicato al baricentro (in viola), e diretto verso il basso. Le altre forze invece sono rappresentate.

La freccia gialla rappresenta la forza centrifuga. Questa risulta dall'inerzia complessiva della macchina, è applicata al baricentro e punta verso l'esterno della traiettoria circolare seguita dalla macchina. Questa forza si traduce in un momento che tende ad inclinare la macchina, che dovrà essere controbilanciato da una forza uguale e contraria, come stabilito dalla seconda legge di Newton. Questa reazione è data dalla risultante del maggior carico sopportato dai pneumatici esterni. Dato che ikl peso totale non cambia, tutto il peso aggiunto ai pneumatici esterni è sottratto a quelli interni. In altre parole, il peso si è spostato verso l'esterno della curva.

Le conseguenze sono molte ed importanti. Un carico non omogeneo sui pneumatici comporta che la tenuta di strada totale si riduca, diminuendo la direzionalità della macchina. Inoltre, il momento che abbiamo citato sopra tende a far inclinare il telaio. In questo esempio la macchina non si inclina, perché non è dotata di sospensioni, come non si inclinerebbe nel caso in cui il baricentro si trovasse sull'asse di rollio. E comunque, l'inclinazione del telaio non modifica la quantità di peso trasferita non cambia (nell'ipotesi che il baricentro non si sposti). Ciò che cambia, invece, è dove viene trasferita la maggior parte del peso. Ceto, in questo esempio è facile: il peso sottratto dalla ruota antriore sinistra va sull'antriore destra, e quello sottratto alla posteriore sinistra va sulla posteriore destra. In altre parole, la macchina è simmetrica e rimane tale poiché non è dotata di sospenzsioni. Ma per una macchina reale la situazione è differente: supponiamo che il retrotreno si inclini molto di più dell'avantreno, a causa del centro di rollio posteriore molto basso, oppure perché le molle sono molto morbide. In questo caso, il carico traferito sulla ruota posteriore destra è maggiore. Certo, un po' di peso verrà anche trasferito sulla antriore destra, ma in misura minore, e la macchina soffrirà di sottosterzo. Se poi aggingiamo un'accelerazione o una frenata, ci sarà un ulteriore trasferimento di peso in senso longitudinale. Questo è il motivo per cui si può compensare il sottosterzo frenando leggermente: in questo modo, infatti, si trasferisce un po' di peso dal posteriore verso l'avantreno, migliorando un po' la direzionalità. Tutto considerato, non è facile determinare dove e quanto peso verrà trasferito. I fattori in gioco sono tanti, come la rigidità delle molle e delle barre anti-rollio, l'altezza da terra dei centri di rollio, la corsa delle sospensioni ecc.

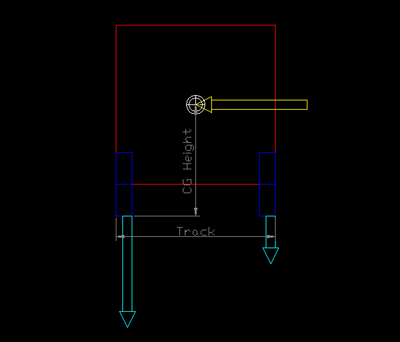
Intanto, vediamo quanto peso viene tasferito. Questo corrisponde alla differenza tra le forze agenti sui pneumatici dei lati opposti, ed è pari al prodotto tra la forza centrifuga (in giallo) e l'altezza da terra del baricentro, diviso per la carreggiata della macchina. La forza centrifuga, a sua volta, espressa in 'g', è data dal prodotto dell'accelerazione radiale per il peso complessivo della macchina. L'accelerazione radiale, a sua volta, è pari al quadrato della velocità angolare del veicolo, diviso per il raggio di sterzata.

Da ciò possiamo concludere che la quantità di peso trasferita è proporzionale all'altezza del baricentro, ed inversamente proporzionale alla carreggiata della macchina. E' per questo che la maggior parte delle macchine da corsa sono quanto più basse e larghe sia ammesso dai regolamenti. In questo modo viene minimizzato il trasferimento di peso, in che a sua volta migliora la trazione complessiva. Essa risulta inoltre proporzionale al peso complessivo, motivo per cui le macchine da corsa sono il più leggere possibile. La quantità di peso trasferita è poi proporzionale a fattori indipendenti dalla macchina, quali la velocità ed il raggio di sterzata istantaneo.

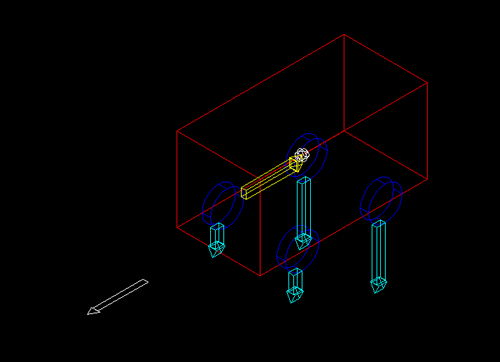
Il discorso è praticamente uguale a quello per il trasferimento di peso laterale, solo nell'altra direzione. Questa volta la macchina sta percorrendo una traiettoria rettilinea (freccia bianca), e sta accelerando. In altre parole, la velocità sta aumentando, o, nei termini usati sopra, il vettore velocità aumenta in modulo e rimane costante in direzione e verso.

Di nuovo non sono state disegnate tutte le forze agenti, ad esempio le forze che spingono la macchina, che agiscono sulle aree di contatto tra i pneumatici ed il terreno, nella stessa direzione della freccia bianca. Anche il peso della macchina è stato sottinteso.

Come sempre, quando un oggetto subisce un'accelerazione, c'è anche una forza d'inerzia applicata nel baricentro CG (in giallo). Ciò crea un momento, che viene compensato dallo spostamento del peso dalle ruote anteriori a quelle posteriori. Tutto il peso sottratto dalle ruote anteriori viene spostato sulle posteriori, e, fintantoché l'accelerazione è rettilinea, ciò avviene in modo simmetrico.

Un carico maggiore sui pneumatici posteriori può far comodo in una macchina a trazione posteriore che sia accelerando in rettilineo, ma, a causa della riduzione del carico frontale, ci sarà un pronunciato effetto di sottosterzo. Si applicano tutti i discorsi fatti al paragrafo precedente: dato che i pneumatici sono caricati in modo diseguale, la trazione totale è minore. Questo è anche il motivo per cui il modo più veloce di percorrere una curva è senza frenare o accelerare. Inutile dire che per far ciò è necessaria una macchina ben bilanciata, né sovrasterzante né sottosterzante. Un'altro aspetto uguale è che l'entità complessiva del trasferimento di peso è indipendente dall'inclinazione del telaio. La macchina probabilmente si inclinerà in avanti in frenata e all'indietro in accelerazione, ma la quantità di peso spostata non cambia. Ciò ovviamente a meno che non cambi di molto l'altezza del baricentro, il che può accadere se le sospensioni hanno un'ampia corsa negativa. Supponiamo che il muso si alzi parecchio, mentre il posteriore non si abbassi granché. In questo caso, il baricentro si alzerà, aumentando la quantità di peso trasferita alle ruote posteriori. E' questo il meccanismo che innesca le sgommate: più il muso si alza, maggiore è la trazione e quindi l'accelerazione, tanto più tende ad alzarsi il muso , e così via, con una specie di 'effetto valanga'.

La formula per calcolare l'ammontare del peso trasferito è molto simile alla precedente. Questa volta è data dal prodotto della forza d'inerzia per l'altezza del baricentro, diviso per il passo della macchina (anziché la carreggiata). La forza d'inerzia è pari al prodotto dell'accelerazione per la massa del veicolo. Perciò, un baricentro basso ed un passo lungo diminuiscono il trsferimento di peso longitudinale. E, come sempre, l'entità del trasferimento è proporzionale all'accelerazione.

Vai al prossimo Capitolo

Vai all'Indice