Qui è raffigurato un oggetto composto di una parte pesante (scura) e di una parte più leggera (chiara), di cui vorremmo determinare il baricentro. Dato che la parte a destra è più pesante, il baricentro si troverà probabilmente spostato a destra rispetto al centro geometrico.
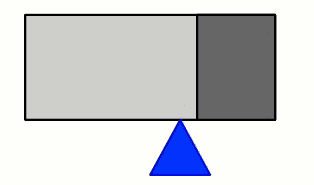
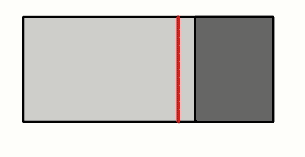
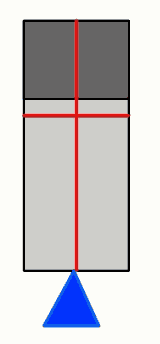
Cerchiamo di tenere l'oggetto in equilibrio su un appoggio a spigolo, e supponiamo che quella indicata sia la posizione in cui rimane in equilibrio. Ora sappiamo che il baricentro è proprio sulla verticale di questa posizione. La linea rossa contiene tutti i punti che erano sulla verticale della posizione di equilibrio, e quindi il baricentro deve giacere su di essa. Adesso seguiamo lo stesso procedimento, ma su un altra dimensione. Di nuovo, possiamo tracciare una linea rossa su cui deve trovarsi il baricentro. 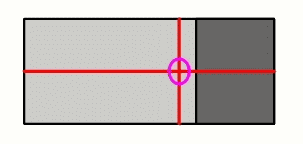Poiché questo era un esempio in due dimensioni, è sufficiente ripetere la procedura due volte, per trovare il baricentro (cerchiato in viola). Per una macchina, che ha tre dimensioni, bisognerà ripeterla tre volte. Il tutto potrebbe presentare qualche difficoltà pratica, ma qui dovrete usare la vostra immaginazione. Una volta nota la posizione del baricentro, possiamo facilmente calcolare il peso sopportato dai pneumatici e la distribuzione dei pesi. 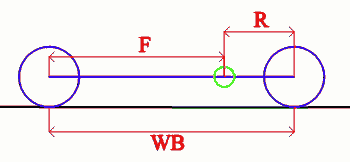Per cominciare, consideriamo la distribuzione longitudinale dei pesi: Il passo WB è la distanza che intercorre tra l'asse anteriore e quello posteriore, F è la distanza tra il baricentro CG (in verde) e l'asse anteriore, mentre R è la distanza tra il baricentro CG e l'asse posteriore. Peso sull'asse anteriore = peso totale ´ (R/WB) Peso sull'asse posterire = peso totale ´ (F/WB) Ovvero, in percentuali: Percentuale di peso anteriore = (R/WB) ´ 100% Percentuale di peso posteriore = (F/WB) ´ 100% Ovviamente, ciò influenzerà il comportamento di guida della macchina: maggior peso sul pneumatico significa infatti maggior tenuta di strada. Quindi, se il baricentro è arretrato, la macchina presenterà una buona trazione sulle ruote posteriori, che è utile se si vuole la massima accelerazione. Se il baricentro è spostato in avanti, la macchina avrà grande direzionalità, ma potrebbe mancare in trazione posteriore, con maggior rischio di andare in testa-coda. In qualche caso, specialmente nelle macchine cosiddette LTO (left turn only) che corrono sui circuiti ovali, è più importante la distribuzione trasversale dei pesi. 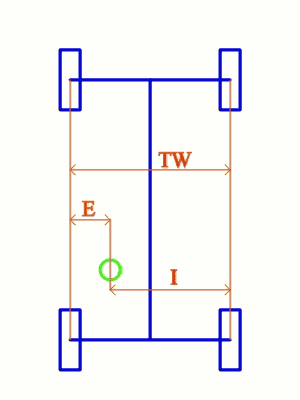E' sostanzialmente la stessa cosa: TW è la carreggiata, la distanza tra le mezzerie dei pneumatici all'altezza dell'asse, E è la distanza tra il baricentro CG (in verde) e la mezzeria dei pneumatici di sinistra, I quella tra il baricentro e la mezzeria dei pneumatici di destra. Se la carreggiata anteriore e quella posteriore differiscono, E ed I devono essere misurate all'altezza del CG. Peso sul lato sinistro = (I/TW) ´ peso totale Peso sul lato destro = (E/TW) ´ peso totale Ovvero, in percentuali: Percentuale di peso a sinistra = (I/TW) ´ 100% Percentuale di peso a destra = (E/TW) ´ 100% Si noti che, se si desidera calcolare il peso sopportato da un dato pneumatico, è necessario moltiplicare il peso totale della macchina per due fattori, uno che dà conto del bilanciamento longitudinale e uno per quello trasversale. Ad esempio: Peso sul pneumatico anteriore sinistro = peso totale ´ (I/TW) ´ (R/WB) Peso sul pneumatico anteriore destro = peso totale ´ (E/TW) ´ (R/WB) Peso sul pneumatico posteriore sinistro = peso totale ´ (I/TW) ´ (F/WB) Peso sul pneumatico posteriore destro = peso totale ´ (E/TW) ´ (F/WB) Si noti che ciò è corretto solo se la macchina non ha regolazioni particolari. Il precarico delle molle dovrebbe essere lo stesso su entrambi i lati della macchina. Di nuovo, se il baricentro non giace sulla mezzeria della macchina, ci saranno conseguenze sul comportamento della stessa: spostarlo a sinistra migliora la capacità di curvare a sinistra, ma renderà molto difficile mantenere una traiettoria rettilinea, specialmente in accelerazione. Anche l'altezza da terra del baricentro è molto importante: determina infatti la tendenza al rollio della macchina e come il peso si distribuisce. Maggiori particolari su questo argomento si trovano al Capitolo 2. Purtroppo, non abbiamo ancora visto tutto: abbiamo trascurato l'inerzia, per la precisione l'inerzia rotazionale. 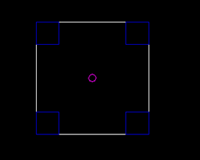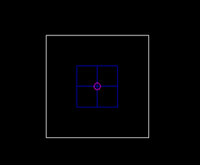Ad esempio: Questi disegni schematizzano due macchine: la prima, a sinistra, ha tutto il peso (in blu) concentrato agli estremi, lontano dal baricentro CG (in viola). La seconda, a destra, ha tutto il peso concentrato nel mezzo, vicino al baricentro. Per il resto, le due macchine hanno lo stesso peso e il baricentro nella stessa posizione. In curva o in frenata, entrambe le macchine trasferiranno la stessa percentuale di peso e si inclineranno di un angolo uguale. Tuttavia, non si comporteranno allo stesso modo, perché il loro momento d'inerzia è differente. La prima macchina reagirà lentamente, si inserirà in curva in modo poco deciso e sarà in generale più riluttante a cambiare direzione. Qualcuno dirà che è lenta, altri che è molto stabile, è la stessa cosa. Il contrario avverà per la seconda macchina: sarà veloce nei cambi di direzione, e apparirà molto agile e quindi anche instabile. Quindi, il momento d'inerzia non cambia l'entità degli spostamenti del telaio, bensì la velocità con cui li compie. E' come brandire una mazza da baseball dotata di una punta molto grossa e pesante: ci vuole un grosso sforzo per metterla in movimento, e una volta che ha preso velocità, è molto difficile cambiarne la traiettoria. Anche il momento d'inerzia può essere calcolato: il momento d'inerzia di un corpo attorno ad un asse è dato dalla somma di tutte le masse elementari che lo compongono, moltiplicate per il quadrato della loro distanza dall'asse stesso. Per corpi dalla forma semplice, come cilindri, cubi e coni, il conto si può fare a mano, ma per applicazioni reali è necessario un sofisticato programma di CAD. Si noti che è importante rispetto a quale asse si calcola il momento d'inerzia. Si consideri il seguente esempio: Questi disegni rappresentano macchine identiche, salvo per la diversa distribuzione dei pesi: la prima ha gli elementi pesanti (in blu) allineati lungo l'asse trasversale (in viola), e la seconda lungo l'asse longitudinale. 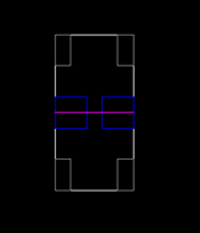Consideriamo la prima macchina: se calcoliamo il momento d'inerzia relativo all'asse trasversale, dovremo moltiplicare tutte le masse per la loro distanza dall'asse al quadrato. In questo caso, la maggior parte della massa verrà moltiplicata per una distanza piccola (al quadrato), ed il risultato sarà piccolo a sua volta. Viceversa, se calcoliamo il momento d'inerzia rispetto all'asse longitudinale (non mostrato in figura), la maggior parte della massa sarà moltiplicata per una distanza grande (al quadrato), ed il risultato sarà a sua volta grande. Quindi, la prima macchina ha un momento d'inerzia molto grande rispetto all'asse longitudinale, e molto piccolo rispetto a quello trasversale. In altre parole, questa macchina reagirà molto lentamente in curva, e si inclinerà lateralmente molto lentamente. D'altra parte, presenterà una spiccata tendenza al beccheggio, cosa che potrebbe essere utile nelle staccate violente, ma la farà rimbalzare molto sulle asperità del terreno, rendendola molto instabile. 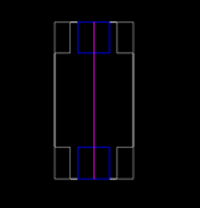Per la seconda macchina vale il discorso opposto: essa presenta una grande momento d'inerzia rispetto all'asse trasversale (non mostrato), e un momento d'inerzia molto piccolo rispetto all'asse longitudinale. Ciò significa che la macchina avrà una spiccata tendenza al rollio e risponderà bene in curva, ma sarà molto stabile in senso longitudinale. Ciò contribuisce a stabilizzare la macchina sulle irregolarità del terreno, mantenendo una buona capacità di inserimento in curva. Forse, a questo punto, capirete perché tanto interesse per il motore centrale nelle macchine reali: il motore è di gran lunga l'elemento più pesante, per cui, posizionandolo centralmente, il momento d'inerzia della macchina è ridotto, a tutto vantaggio della maneggevolezza. 
$Revision: 1.2 $ $Date: 2000/08/19 20:13:53 $