Alla ricerca della soluzione simbolica

La soluzione simbolica dovrebbe diventare il santo Graal che gli alunni cercano, spinti dalle considerazioni già fatte sull'esattezza e da altre che si presentano, come la necessità di discutere la risolubilità del problema al variare dei dati o la necessità di risolvere problemi con più incognite.
In effetti l'approdo ai sistemi di equazioni, in cui non sia banalmente eliminabile una incognita, pone qualche problema ai metodi numerici: è ancora possibile fare ricorso al foglio elettronico, però le incognite non devono essere più di due, e lo stesso vale per gli strumenti grafici; per questi, tra l'altro, non bastano più i semplici programmi che disegnano le funzioni y=f(x) , ma bisogna avere quelli che graficano decentemente le funzioni implicite di due variabili; in ogni caso credo che sia istruttivo l'uso di questi strumenti, anche se a volte fanno venir voglia di qualcosa di più generale e quindi spingono verso l'approccio simbolico [che comunque non è più potente al di là del caso lineare, però più adatto a trattare molte incognite]. Il ricorso ad algoritmi iterativi mi sembra istruttivo, ma difficilmente proponibile per la mole di calcoli che richiede.

A volte io rappresento agli studenti la situazione in questo modo: quando si affronta un problema con l'analisi noi abbiamo una macchinetta che, per ogni numero che buttiamo dentro, ne sforna un altro; vogliamo trovare il numero da inserire perché esca zero. Naturalmente possiamo tentare a caso, però avremmo risolto la questione se potessimo costruire una macchinetta che fa il contrario della prima e per ogni numero sfornato da essa ci restituisse quello che abbiamo inserito: potremmo chiamarla  formula inversa o qualcosa di simile. La domanda è: in quali casi è possibile costruirla ? e come ?

Alla fine della scuola media gli studenti sono pratici di formule inverse, che spesso trovano già confezionate nel libro o dall'insegnante. In ogni caso sono spesso invitati a ragionare a ritroso, perché generalmente i problemi assegnati proprio questo richiedono: infatti parecchi falliscono proprio per mancanza di questa abilità. Però la crescita di questa abilità mi sembra che sia lasciata a madre natura, mentre penso che si potrebbe fare qualcosa per renderne consapevole l'allievo e guidare quelli un pò svantaggiati. Per esempio si potrebbe insistere un pò sull'inversione delle operazioni elementari, evidenziando in particolare i due casi 'anomali' del sottraendo e del divisore; si potrebbe poi passare all'inversione di sequenze di operazioni, aiutandosi magari con schemi strutturali come il seguente, che spesso sono usati dalle maestre.

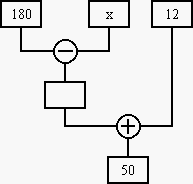
Utilizzando questo schema o simili l'allievo si rende conto che l'inversione è facile se in ogni nodo [operazione] vi è una sola casella incognita, il che si verifica se l'incognita non viene usata più di una volta nei calcoli. In effetti i problemi assegnati alla scuola media soddisfano questa condizione, anche se a volte il numero di operazioni da invertire è abbastanza alto.
Gli allievi di normale abilità effettuano facilmente l'inversione, anche senza bisogno di schemi, però rischiano di acquisire la falsa opinione che essa si possa sempre effettuare, da cui credo la tendenza ad affrontare tutti i problemi cercando una via diretta verso la soluzione. Ritengo che non sarebbe male presentare già alla scuola media situazioni non elementarmente invertibili, invitando gli allievi a rendersi conto della eccezionalità del caso.

Nella pratica didattica ho visto che funziona abbastanza bene un esercizio di questo tipo:
partendo da un problema risolvibile per sintesi come per esempio:
<<Se un vestito costa di listino 300 e ottengo il 15% di sconto, quanto lo pago ?>>
si invitano gli allievi a costruire l'espressione o il diagramma strutturale delle operazioni svolte e poi a formulare i problemi 'inversi' derivabili da questo:
<<Se un vestito costa 300 e lo pago 250, che percentuale di sconto ho ottenuto ?>> e
<<Se ho pagato 250 un vestito dopo aver ottenuto il 15% di sconto, qual era il prezzo di listino ?>>
Dopo di che si riutilizza lo schema del primo, mettendo opportunamente le incognite e i dati.
Gli allievi non tardano a rendersi conto che mentre il primo di questi due è facile da risolvere, perché l'incognita è usata una volta sola, il secondo lo è molto meno, perché viene usata due volte: e infatti di solito sbagliano la risposta.