Procedure iterative come trial & error organizzato

Un'altra interessante via di sviluppo porta verso gli algoritmi iterativi del calcolo numerico.

La cosa nasce dall'osservazione che dopo due tentativi abbiamo informazioni sufficienti per orientare oculatamente il terzo: infatti possiamo vedere se l'errore varia concordemente con l'incognita e possiamo anche stimare il rapporto tra le loro variazioni. Gli studenti, che hanno già una certa familiarità con le proporzioni, trovano abbastanza facile effettuare una interpolazione lineare per ottenere il terzo tentativo dai primi due. Lo schema che i miei allievi trovano più chiaro è questo:

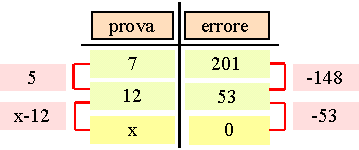
Se si ha l'avvertenza di lavorare con equazioni lineari, gli allievi trovano con sorpresa che al terzo tentativo hanno la soluzione, e anche esatta. 
Riguardo all'esattezza in realtà scoprono che, se durante il procedimento non eseguono mai le divisioni, alla fine ottengono una frazione che riduce l'errore esattamente a zero, mentre se eseguono una divisione approssimata anche la soluzione viene approssimata: questo li introduce a considerare come mai i risultati proposti dal libro sono di solito sotto forma frazionaria invece che decimale. Ciò che ne dovrebbero trarre è l'idea che l'armamentario del calcolo con frazioni non è altro che una tecnica per evitare per quanto possibile le divisioni, che tra le quattro operazioni sono le uniche a dare risultati approssimati. Lo stesso vale naturalmente per le radici, che pure introducono approssimazioni, e questo dovrebbe giustificare l'altro argomento, caro ai docenti ma poco agli studenti, del calcolo con radicali.
Quanto al valore da attribuire ai due tipi di soluzione, approssimata ed esatta, dovrebbero comprendere che mentre della prima non si può più aumentare la precisione, a meno di non ripetere tutti i calcoli, della seconda si può ancora scegliere la precisione a piacere al momento di effettuare la divisione o il calcolo della radice.

Degli algoritmi finora visti, questo dell'interpolazione lineare è l'unico in grado di fornire una soluzione esatta, o simbolica, come si usa dire.  Il significato del termine 'simbolica' riferito alla soluzione significa questo: ho una formula che mi permette di calcolare il valore della soluzione con un numero ben definito di operazioni e con la precisione che voglio.
Gli studenti si rendono ben conto dell'importanza di avere una formula che dà la soluzione, in quanto essa traccia una via diretta dai dati del problema alla risposta  e quindi risolve una volta per tutte i problemi simili a quello in esame ma aventi dati diversi; tanto che i dati si potrebbero anche indicare con simboli, come lettere. 
L'interpolazione lineare consente di arrivare alla formula anche agli studenti in difficoltà con il calcolo letterale, in quanto non ne dipende, o solo per la parte che richiede di mettere in un'unica espressione varie operazioni.

Prima che gli studenti si convincano che questa tecnica risolva tutti i problemi, è bene mostrarne i limiti applicandola ad una equazione non lineare: si ha così modo di far capire che il metodo funziona in un ambito circoscritto, come del resto tutti quelli che portano a soluzioni simboliche, e che quindi c'è posto anche per altre tecniche.

Il caso lineare è comunque rilevante nella pratica e sarà bene metterlo in evidenza: per esempio in ambito economico la maggior parte dei problemi è lineare. È possibile anche caratterizzare la linearità dal punto di vista grafico, introducendo lo studio degli allineamenti di punti e delle rette nel piano cartesiano: la tecnica dell'interpolazione consente di farlo in modo semplice anche se poco convenzionale.

A partire dal fallimento dell'interpolazione nel caso non lineare si possono introdurre, avendone tempo, algoritmi iterativi basati sulla ripetizione dell'interpolazione [metodo delle corde], che andrebbero però programmati su computer, dato che rischiano di stancare per la noia dei calcoli ripetitivi, e che comunque non portano più alla soluzione simbolica.