| Quasi.
Cinderella segue una sua logica, che
non sempre soddisfa tutte le nostre aspettative. Ripartiamo dal nostro esempio, vedendo se sia possibile evitare di introdurre tra i dati la retta. Questo crea una notevole indeterminazione negli elementi finali richiesti, in quanto va bene uno qualsiasi dei punti di un cerchio: si può capire che Cinderella sperimenti un certo disorientamento, ma è più stupefacente che in qualche modo riesca a gestire anche questa situazione, pur se non in modo perfetto. |
|
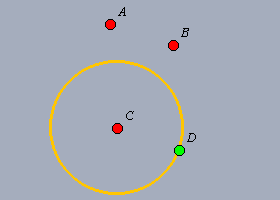
| Definiamo come dati iniziali i punti A,B,C
e come unico elemento finale il punto D, che abbiamo ancorato al
cerchio giallo, disegnato, come prima, utilizzando lo strumento
"compasso".
Salviamo l'esercizio, e proviamo a risolverlo come prima. |
 |
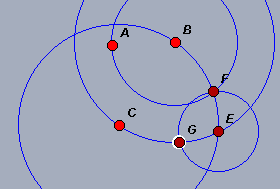
| Questa volta lo risolviamo alla Mascheroni,
usando solo i cerchi, però non fa differenza. Ciò che interessa
osservare è che il punto G della figura risolve il problema,
però Cinderella non lo
considera una soluzione. Probabilmente il motivo è che si aspetta un
punto libero sul cerchio e non un punto vincolato. Proviamo a vedere se è così. |
 |
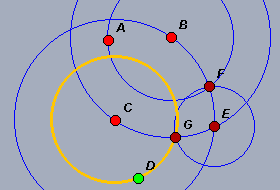
| Completando la costruzione con il cerchio
giallo e piazzandovi sopra un punto in una posizione qualsiasi, il
problema viene considerato risolto. Se ne deduce che in qualche modo Cinderella controlla anche la tipologia degli elementi, distinguendoli tra liberi e vincolati. Su questo il manuale non parla, e quindi bisogna cercare di farsi un'idea con qualche prova. |
 |
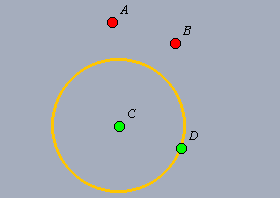
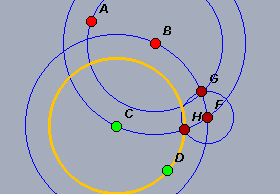
| Comunque Cinderella
si mostra duttile nel trattare i casi indeterminati, come, per esempio,
se si volesse partire solo da A e B e si chiedesse di
costruire altri due punti qualsiasi, C e D, distanti tra
loro come A da B. Nella figura a fianco, A e B sono gli elementi iniziali e C e D costituiscono la soluzione. C è un punto libero sul piano e D è libero di muoversi sul cerchio giallo: essi quindi non hanno una posizione prefissata, e neppure il cerchio giallo. |
 |
| Nella figura a fianco si vede che cosa
succede: non appena si piazza un punto libero sul piano, il programma lo
chiama C e lo identifica con il primo elemento della soluzione.
Poi tutto procede come nel caso precedente.
Questo mostra che l'algoritmo di verifica di Cinderella non si basa sulla mera coincidenza spaziale di elementi, ma su una intelligente verifica di relazioni, non molto lontana dal modo di ragionare umano. |
 |
Continuando ad esplorare i casi
in cui il programma si discosta dal nostro modo di lavorare, è utile
far presente il trattamento riservato alle coordinate. Tramite lo
strumento "calamita" 
è possibile piazzare con facilità i punti su coordinate intere; però
questo non è utilizzabile negli esercizi: definendo come soluzione per
es. il punto (1,2) e piazzandoci sopra esattamente un punto al momento
di risolvere l'esercizio, non viene rilevata la coincidenza tra i due.
Questo impedisce di produrre alcuni semplici esercizi sulle coordinate;
però si può rimediare con qualche semplice trucco. |
|
