Il moto
(rettilineo, curvilinio e armonico)

121. Per imprimere a un preparato un'accelerazione molto grande (per separare più rapidamente i componenti), nei laboratori di analisi vengono impiegate comunemente delle centrifughe, che realizzano un moto circolare uniforme molto rapido. Volendo imprimere a un preparato un'accelerazione di 100 m/s², servendosi di un asse di rotazione capace di 600 giri al minuto, quanto deve essere lungo il braccio della centrifuga?
[

122. Un sasso legato a una fune si muove, con velocità di modulo costante, lungo una circonferenza di raggio r = 50 cm con una frequenza f= 5,0 Hz.
a) Calcola il modulo dell'accelerazione centripeta dell'oggetto.
b) Se il sasso percorresse la stessa circonferenza a una velocità doppia della precedente, di quanto varierebbe la sua accelerazione centripeta?

123. Nel passare il pallone a un compagno, un giocatore di pallacanestro descrive con il braccio un arco di circonferenza di 60° in 0,75 s, a velocità approssimativamente costante.Supponendo un braccio lungo 80 cm.
a) Calcola con quale velocità v viene lanciato il pallone.
b) Quale accelerazione a viene impressa al pallone dal braccio del giocatore?

124. Una formica sale e scende continuamente da un formicaio che si trova sotto terra. Si può dire che compie un moto armonico?

125. Se un punto materiale si muove di moto circolare uniforme su una circonferenza, il cui raggio misura 5,0 cm, percorrendola 15 volte al minuto, qual è la legge del moto armonico della sua proiezione sull'asse orizzontale?

126. Supponi di poter considerare moto armonico semplice il moto su-giù di un pistone del motore di un'automobile. Il pistone ha una corsa complessiva di 8 cm e il motore va a 2.4 • 10³ giri al minuto.
a) Calcola il modulo dell'accelerazione istantanea a del pistone, nel punto più alto del suo moto.
b) Calcola la velocità v quando, invece, si trova a metà della sua corsa.

127. Un ragazzo maleducato lancia dal finestrino di un treno, nella direzione del moto, una lattina vuota, imprimendole una velocità iniziale di 20 m/s. Il treno viaggia in quel momento a 120 km/h. Qual è la velocità iniziale della lattina rispetto al suolo?

128. Un aereo è in rotta di collisione con un missile. Le loro velocità sono parallele e rispetto al suolo valgono rispettivamente 2 mach e 4 mach (1 mach equivale alla velocità del suono nell'aria, che puoi trovare cliccando qui). Con quale velocità l'aereo vede avvicinarsi il missile?

129. Un osservatore A, fermo rispetto al suolo, vede delle gocce di pioggia cadere verticalmente. Un secondo osservatore B, invece, si trova all'interno di un'automobile in moto e determina che le gocce di pioggia formano un angolo a = 60° rispetto alla verticale al suolo. L'automobile sta viaggiando a una velocità v₀= 50 km/h. Determina il modulo della velocità v delle gocce di pioggia rispetto all'osservatore A e il modulo della velocità v' rispetto all'osservatore B.

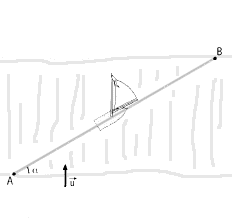
130. Un'imbarcazione descrive una traiettoria rettilinea AB, che forma un angolo a = 30° con la sponda del fiume, partendo da un punto A posto su una riva del fiume per arrivare a un punto B posto sull'altra riva. Il vento soffia perpendicolarmente alle sponde del fiume con una velocità in modulo, rispetto al suolo, di u = 8 nodi. In queste condizioni la bandiera posta sull'albero dell'imbarcazione si onerila perpendicolarmente alla traiettoria.
a) Determina il modulo della velocità v, rispetlo al suolo, dell'imbarcazione.
b) Dai dati t'ornili è possibile ricavare la velocità dell'acqua del fiume?

131. Una pallina è appesa al soffitto e viene falta oscillare nello spazio. La scena viene illuminala lateralmente con due lampade, che si trovano alla slessa altezza della pallina e che sono disposte come è illuslrato nella figura in modo da proiettare l'ombra della pallina su due schermi tra loro perpendicolari. Su entrambi gli schermi l'ombra della pallina compie un moto armonico con periodo T = 2 s e ampiezza d = 10 cm. Nell'istante in cui uno dei due moli giunge a un estremo dell'oscillazione, l'altro si trova nel punto medio. Determina in modo sia qualitalivo che quantitativo il tipo di moto della pallina.

132. In un fiume di larghezza h si può grossolanamente assumere che la velocità dell'acqua aumenti proporzionalmente alla distanza dalle sponde e raggiunga il valore massimo V₀ nel centro del fiume. In prossimità delle due sponde la velocità dell'acqua è nulla. Un'imbarcazione si sta muovendo da una sponda all'altra con una velocità V. relativa all'acqua, che è costante e perpendicolare alla corrente fluviale.
a) Determina di quanto la corrente sposta la barca che attraversa il fiume.
b) Determina, inoltre, la traiettoria dell'imbarcazione.

133. Un disco rotola senza scivolare sopra un piano orizzontale con una velocità costante v_tr

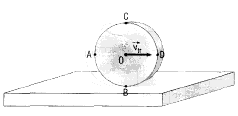
a) Dimostra che il modulo della velocità lineare di rotazione di ogni punto del bordo del disco rispetto al centro 0 è uguale alla velocità traslazionale del disco;
b) Trova il modulo e la dirczione della velocità dei punti A, B. C e D posti sul bordo del disco rispetto a un osservatore che si trova sopra il piano orizzontale;
c) Individua quali punti del disco hanno lo stesso modulo della velocità del centro 0 del disco rispetto a un osservatore che si trova sopra il piano orizzontale.

134. Sullo schermo di un cinema è mostrato un ciclista impegnato in una gara a cronometro. Il ciclista fa uso di
una moderna bicicletta, le cui ruote anteriori hanno N₁ = 8 raggi e il diametro pari a 2r = 0.6 m. Quelle posteriori, invece, hanno un diametro 2R = 3r Assumi che le ruote non scivolino sulla strada. II film e proiettato con una velocità di 24 fotogrammi al secondo.
a) Trova la minima velocità con cui il ciclista dovrebbe muoversi affinchè le ruote anteriori della bicicletta appaiano ferme sullo schermo.
b) Determina il numero minimo di raggi. N₂. che le ruote posteriori dovrebbero avere per sembrare ferme contemporaneamente a quelle anteriori.

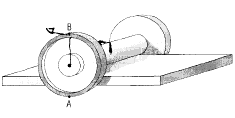
140. Un cilindro, di raggio r. rotola su un piano e un disco applicato a un suo estremo sporge dal piano stesso, come è mostrato in figura. Il raggio del disco è R (R >> r). Il cilindro rotola, senza scivolare, con una velocità costante v.
a) Determina la velocità istantanea, rispetto al piano, dei punti A e B posti sul bordo del disco.
b) Individua quali punti del disco hanno una velocità istantanea, rispetto al piano, di modulo pari a v.

Il moto - - - preview . . . pag 7 . . . next