Il moto
(rettilineo, curvilinio e armonico)

101. Un oggetto si muove su una traiettoria circolare. Determina di quanto varia la velocità quando l'oggetto passa da un punto P della circonferenza al punto Q, diametralmente opposto a P. sapendo che i due vettori v_p e v_q hanno lo stesso modulo v.
[Dv= -2v_p]

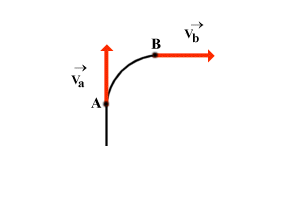
102. Un treno percorre in 10 s la curva da A a B cambiando la velocità da v_a a v_b . I due vettori sono perpendicolari e hanno un'intensità di 30 m/s. Calcola la direzione, il verso e l'intensità dell'accelerazione media.

[a= 4,2 m/s²; assumendo come asse di riferimento la direzione v_a e come verso positivo sempre quello di v_a, allora l'accellerazione media forma con quest'asse un angolo a = 135° a desta rispetto al verso v_a]

103. Disegna i vettori velocità di un punto materiale che si sposta lungo una circonferenza, alla velocità costante di 10 cm/s, nei punti A e B mostrati nella figura seguente. Calcola poi il modulo della variazione di velocità che ha subito il punto materiale passando dal punto A al punto B.

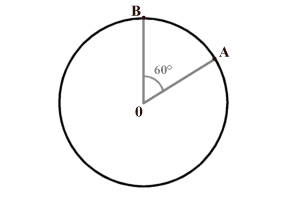
[0,1 m/s]

104. Sapendo che il punto materiale considerato nell'esercizio precedente passa da A a B in 5 secondi, calcola la sua accelerazione media.
[2 com/s²]

105. Calcola il periodo e la velocità scalare di un punto che si trova sul bordo di un disco a 33 giri (la frequenza è quindi 33 giri al minuto). Il diametro del disco è 30 cm.
Sapendo che l'etichetta ha un diametro di 10 cm, ripeti lo stesso calcolo per un punto che si trova vicino al bordo dell'etichetta.
[1,8s; 0,52 m/s; 0,17m/s]

106. Calcola la velocità scalare di un punto materiale che percorre una circonferenza di raggio r = 30 cm con la uenza di 4.0 Hz.
[7,5 m/s]

107. Una motocicletta, le cui ruote hanno un diametro di 64 cm. percorre 72 km in 1 ora.
a) Calcola quanti giri. G. hanno fatto le due ruote.
b) Calcola il periodo medio T e la frequenza media f con cui hanno girato le ruote.
c) Determina infine il modulo i della velocità di un punto che si trova sul battistrada dello pneumatico rispetto all'asse della ruota.
[G @ 3,6 • 10⁴; T= 0,1s; f =10 Hz; v = 20m/s]

108. Determina la misura in radianti dell'angolo che stacca un arco pari a 5/7 della circonferenza.
[10p/7 rad]

109. Determina la misura in radianti dell'angolo che stacca un arco lungo 4.7 m su una circonferenza di raggio pari a 13.0 m.
[0,36 rad]

110. Calcola la lunghezza l di un arco di ampiezza 30° e il cui raggio è lungo r = 18 cm.
[l=9,4cm]

111. Determina la velocità angolare di una ruota che gi ra alla frequenza di 150 Hz.
[942 rad/s]

112. Determina il periodo e la frequenza di rotazione di un'elica con una velocità angolare di 18800 rad/s.
[2992,1 Hz; 3,3421 • 10^-4]

113. Calcola la velocità angolare w della Terra attorno al proprio asse nel sistema di riferimento del Sole. Determina inoltre la misura in gradi dell'angolo a descritto in un'ora da un punto posto sull'Equatore terrestre nel moto di rotazione diurna.
[w = 7,3 • 10^-5 rad/s; a=15°]

114. Due pulegge, montate sugli assi A e B, sono collegate con una cinghia che trasmette il moto rotatorio da A a B. Una puleggia di diametro D_b = 80 cm è posta sull'asse B che deve ruotare a f_b= 500 giri al minuto; mentre la velocità di rotazione dell'asse A è f_a = 5000 giri al minuto. Quale deve essere il diametro D_a della puleggia da collocare sull'asse A?

[D_a= 8cm]

115. Un trattore si sta muovendo con una velocità v₀ = 18 km/h. Per cambiare direzione, il conducente deve frenare uno dei due cingoli fino a quando la ruota motrice di questo cingolo si muove con una velocità v₁ = 14 km/h. La distanza tra i due cingoli è d = 1,5 m. Trova il raggio R dell'arco descritto dal punto centrale del trattore.
[R= 6m]

116. Calcola l'accelerazione centripeta di un oggetto che viaggia, a velocità costante, lungo una circonferenza di raggio r = 5 cm con la frequenza di 5 Hz.
[50m/s²]

117. Un oggetto, che si muove di moto circolare uniforme, descrive una circonferenza di 20 cm di diametro e fa 2 giri al secondo. Che distanza percorre in mezz'ora? Qual è l'accelerazione del suo moto?
[2,3 km; 16 m/s²]

118. Un punto gira alla velocità di 0,3 m/s. Sapendo che il periodo è uguale a 1 min. calcola l'accelerazione centripeta del punto.
[3•10^-2 m/s²]

119. Un'automobile si muove di moto uniforme su una pista circolare di raggio r alla velocità v. Di quanto aumenta la sua accelerazione centripeta se la velocità raddoppia?
[4 volte]

120. Un oggetto percorre una circonferenza di raggio r alla velocità v. Se percorresse alla stessa velocità una circonferenza di raggio pari a r/2, di quanto aumenterebbe la sua accelerazione centripeta?
[2 volte]

Il moto - - - preview . . . pag 6 . . . next