Calcolare il tempo dopo il quale le due automobili hanno la stessa velocità e gli spazi percorsi in tale intervallo di tempo. Dopo quanto tempo le due automobili si ritrovano insieme?
[3s; 18 m; 45 m; 6 s]
Il moto
(rettilineo,
curvilinio e armonico)
81. Un punto materiale, partendo da fermo, si muove sopra una
retta con accelerazione costante uguale a 2 m/s2.
Determinare il diagramma tempo-velocità e tempo-spazio e la
velocità raggiunta dopo aver percorso la distanza di 784 m.
[56 m/s]
82. Un'automobile viaggia alla velocità di 72 km/h. Premendo
il pedale dell'acceleratore la velocità aumenta con
accelerazione costante fino a 144 km/h.
Sapendo che lo spazio percorso durante la fase di accelerazione
è 300 m, calcolare l'accelerazione e l'intervallo di tempo in
cui si è avuta la variazione di velocità.
[2,0 m/s2; 10 s]
83. Un punto materiale si muove di moto uniformemente
accelerato con accelerazione uguale a -0,5 m/s2 e
velocità iniziale 30 m/s. Determinare dopo quanto tempo il punto
materiale inverte il moto e la distanza percorsa durante questo
intervallo di tempo.
Rappresentare inoltre i diagrammi tempo-spazio e
spazio-velocità.
[60 s; 900 m]
84. Un elettrone è accelerato uniformemente da fermo fino
alla velocità di 4,0 • 107 m/s per un percorso
di 0,10 m.
Calcolare il valore dell'accelerazione e il tempo impiegato a
raggiungere la velocità finale.
[8,0 • 1015 m/s2; 5,0 • 10-7
s]
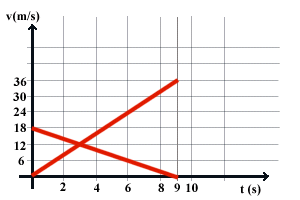
85. Un'automobile parte da ferma su una strada nello stesso
istante in cui transita una seconda automobile alla velocità di
18 m/s. I diagrammi velocità-tempo delle due automobili sono
rappresentati in figura.
Calcolare il tempo dopo il quale le due automobili hanno la
stessa velocità e gli spazi percorsi in tale intervallo di
tempo. Dopo quanto tempo le due automobili si ritrovano insieme?

[3s; 18 m; 45 m; 6 s]
86. Un'automobile sta viaggiando alla velocita di 24 m/s,
quando improvvisamente si presenta a 50 m un ostacolo.
L'autista, azionando i freni, riesce a ottenere istantaneamente
un moto uniformemente ritardato con decelerazione uguale a - 6
m/s2. Stabilire se l'automobile investe l'ostacolo.
Un'automobile mentre viaggia alla velocità di 40 m/s inizia a
rallentare con decelerazione costante uguale a -2 m/s2
fino a fermarsi. Calcolare lo spazio percorso e l'intervallo di
tempo impiegato per fermarsi. Rappresentare inoltre i diagrammi
tempo-velocità e velocità-spazio.
[400 m; 20 s]
87. Un autista mentre viaggia con la sua automobile alla
velocità di 108 km/h, si accorge della presenza di un cane alla
distanza di 160 m. Se i riflessi nervosi consentono all'autista
di iniziare la frenata con un ritardo di 0,2 s, calcolare lo
spazio percorso sapendo che l'automobile si ferma dopo 10 s
dall'inizio della frenata, nell'ipotesi che il moto durante la
frenata sia stato uniformemente ritardato.
Farà in tempo l'autista a evitare di investire il cane?
[156m; sì]
88. Un'automobile lanciata alla velocità costante di 180 km/h
è costretta a fermarsi. Supponendo che occorrano 0,2 s affinchè
i riflessi nervosi consentano all'autista di iniziare a frenare,
calcolare lo spazio percorso dall'istante in cui il guidatore è
costretto a fermarsi, nell'ipotesi che durante la frenata il moto
sia uniformemente ritardato con decelerazione - 10 m/s2.
[135 m]
89. Un'automobile lanciata a velocità v0 è
costretta improvvisamente a fermarsi perché si presenta un
ostacolo a distanza d. Supponendo che i riflessi nervosi
dell'autista consentano di iniziare la frenata dopo un intervallo
di tempo à.t, nell'ipotesi che durante la frenata il moto sia
uniformemente ritardato con decelerazione a, trovare la
condizione cui devono soddisfare i parametri v0 , Dt , a e d affinchè l'automobile non
investa l'ostacolo.
[ v0 • Dt - v02
/ 2a < d]
90. Calcolare il valore massimo che può avere la velocità di
un'automobile affinchè non investa un ostacolo presentatesi
improvvisamente a distanza d, nell'ipotesi che l'autista inizi a
frenare con un ritardo Dt e con
decelerazione costante a.
[ vmax = a • Dt + ((a
• Dt)2 - 2 a • d)1/2]
91. Un'automobile che si muove di moto uniformemente vario
lungo un rettilineo percorre un primo spazio s = 100 m in un
tempo t1 = 5,0 s e successivamente un secondo spazio s2
uguale al primo nel tempo t2 = 15 s.
Calcolare:
a) l'accelerazione dell'automobile;
b) la velocità iniziale espressa in km/h.
Rappresentare il diagramma della velocità in funzione del tempo.
[- 1,3 m/s2; 1,3 • 102km/h]
92. Un mobile si muove di moto uniformemente vario partendo
dalla quiete con accelerazione a. Una massa m possiede una
velocità espressa, in funzione dello spazio s percorso, dalla
relazione seguente: v = (g•s)1/2.
Si domanda per quale valore di a i due movimenti avvengono con la
stessa velocità.
[g/2]
93. Dimostrare la legge di Galileo secondo la quale gli spazi percorsi da un grave in caduta libera nei successivi intervalli di tempo di 1 s sono direttamente proporzionali alla successione dei numeri dispari 1, 3, 5, 7, ...
94. Un grave lanciato verticalmente verso l'alto con velocità
iniziale uguale a 9,8 m/s raggiunge l'altezza massima e dopo
ricade al suolo. Rappresentare graficamente il diagramma della
velocità in funzione del tempo nell'ipotesi che l'attrito sia
trascurabile.
Il diagramma richiesto, gli assi coordinati e l'ordinata estrema
individuano due triangoli. Qual è il significato fisico delle
due aree?
95. Un proiettile viene sparato verticalmente verso l'alto con
velocità iniziale uguale a 392 m/s.
Calcolare l'altezza massima raggiunta e il tempo impiegato a
raggiungerla, trascurando la resistenza dell'aria.
[ 7840 m; 40s]
96. Un proiettile viene sparato lungo la verticale verso
l'alto. Determinare la velocità di lancio e l'altezza del punto
per cui passa in ascesa e in discesa rispettivamente dopo 4 s e 8
s ed eseguire una verifica dei risultati trovati.
[58,8 m/s; 156,8 m]
97. Un sasso viene lanciato verticalmente verso l'alto con
velocità v0.
Determinare la condizione cui devono soddisfare parametri v0
e h affinchè il sasso passi per il punti all'altezza h.
Quante volte passa?
[ una volta per h = v02 /2g; due volte per
h < v02 /2g]
98. Un prestigiatore si esibisce in una stanza. In un certo
momento dello spettacolo egli lancia verticalmente verso l'alto
una palla che dopo 1 s raggiunge il soffitto con velocità nulla.
Calcolare: a) la velocità iniziale con la quale lancia la palla;
b) l'altezza del soffitto.
[9,8 m/s; 4,9 m]
99. Se il prestigiatore dell'esercizio precedente lancia una
seconda palla verso l'alto con la stessa velocità iniziale
nell'istante in cui la prima è sul soffitto, quanto tempo dopo
il lancio della seconda palla una passa accanto all'altra? In
tale istante a che distanza si trovano le due palle al di sopra
delle mani del prestigiatore?
[0,37 s: 2,02 m]
100. Due gravi vengono lanciati verticalmente verso l'alto da
uno stesso punto, entrambi con velocità iniziale 9,8 m/s.
Sapendo che tra i due lanci intercorre un intervallo di tempo di
1 s, determinare dopo quanto tempo dal primo lancio i due gravi
si incontrano.
[15 s]