[20 m; 42 m; 10,5 m/s]
Il moto
(rettilineo,
curvilinio e armonico)
61. Un giovane, nell'intervallo di tempo di 4 h, percorre 6 km
durante la prima ora e 3 km durante la seconda ora. Dopo essersi
riposato per 1 h, percorre 5 km durante la quarta ora. Calcolare
la velocitÓ media durante: a) le prime due ore; b) le prime tre
ore; c) l'intero intervallo di tempo di 4 h.
[4,5 km; 3 km/h; 3,5 km/h]
62. Due atleti, Mario e Franco, stanno facendo una corsa.
Franco parte 16 m dietro Mario correndo alla velocitÓ media di 9
m/s. Se Mario corre alla velocitÓ media di 8 m/s, calcolare dopo
quanto tempo Franco raggiunge Mario e lo spazio percorso da
Franco in tale intervallo e tempo.
[16s; 144 m]
63. Risolvere il precedente esercizio nel caso in cui Franco
parte con un ritardo di 4 s rispetto a Mario.
[52 s; 432 m]
64. Per un treno espresso da Bologna ad Ancona si ricava, da un orario delle FF.SS., la seguente tabella:
| tragitto | km | tempo impiegato |
| Bologna-Forlý | 65,0 km | 42,0 min |
| Forlý-Cesena | 18,0 km | 12,0 min |
| Cesena-Rimini | 29,0 km | 18,0 min |
| Rimini-Pesaro | 33,0 km | 59,0 km |
| Pesaro-Ancona | 20,0 min | 37,0 min |
Determinare il diagramma orario, sapendo che in ogni stazione
effettua una sosta di 3 min. Calcolare inoltre le velocitÓ medie
nei cinque tratti percorsi.
[92,8 km/h; 90,0 km/h; 96,7 km/h; 99,0 km/h; 95,7 km/h]
65. Un treno si muove alla velocitÓ costante di 15 m/s per 2
s, successivamente si muove per 4,0 s con accelerazione costante
uguale a 2,0 m/s2. Dal grafico velocitÓ-tempo del moto del treno
calcolare la velocitÓ dopo 5,0 s e la distanza percorsa in tale
tempo.
[21 m/s; 84 m]
66. Una Fiat Uno viaggia su un'autostrada alla velocitÓ
costante di 120 km/h. Una Lancia Thema s'immette nella stessa
autostrada e allo stesso casello dopo un'ora muovendosi alla
velocitÓ costante di 180 km/h. Rappresentare i diagrammi orari
delle due automobili e determinare graficamente l'intervallo di
tempo, a partire dall'ingresso della Lancia nell'autostrada, dopo
il quale avviene il sorpasso. Qual Ŕ la distanza percorsa dalle
due auto nel momento del sorpasso?
[2h;360km]
67. Dall'analisi dei diagrammi orari delle automobili
dell'esercizio precedente ricavare la distanza tra le due
automobili in funzione del tempo a partire dall'istante in cui la
Lancia fa il suo ingresso in autostrada. Qual Ŕ la pendenza del
grafico ottenuto? E la sua equazione?
[-60km/h;d=120-60t]
67. Un'automobile viaggia in alcuni intervalli di tempo con le velocitÓ e per le durate indicate nella tabella seguente:
intervallo di tempo |
1 |
2 |
3 |
4 |
velocitÓ (km/h) |
80 |
100 |
120 |
60 |
durata dell'intervallo (h) |
2 |
2 |
1 |
3 |
Rappresentare il diagramma orario dell'automobile e
determinare graficamente lo spazio percorso. Calcolare la
velocitÓ media sull'intero percorso.
[760 km: 95 km/h]
68. Un corpo si muove lungo l'asse x con legge oraria x = t2
- 40 t, con x espresso in metri e t in secondi. Determinare la
velocitÓ in funzione del tempo e la distanza massima percorsa
dal corpo allontanandosi a sinistra dell'origine. Calcolare
inoltre la velocitÓ con la quale il corpo passa di nuovo per
l'origine dopo l'istante iniziale.
[v = 2t- 40; - 400 m; 40 m/s]
69. Un corpo si muove lungo l'asse x con velocitÓ espressa in
funzione del tempo dalla relazione v = 10 - 5t, con v misurata in
metri al secondo e t in secondi. Calcolare lo spazio percorso in
funzione del tempo e quello percorso fino a quando il corpo si
arresta. _
[s = 10t - 5/2 t2; 10 m]
70. Un'automobile, che sta viaggiando alla velocitÓ di 20 m/s
sull'autostrada da Ancona a Bologna, a 2 km dall'uscita di Ancona
Nord, inizia ad accelerare di 0,2 m/s2 per 60 s.
Calcolare la velocitÓ al termine dei 60 s e la distanza da
Ancona Nord alla quale si trova al termine di questo intervallo
di tempo.
[32 m/s; 440 m]
71. Un'automobile passa alla velocitÓ di 30,0 m/s davanti a
un'auto della polizia, ferma per il controllo della velocitÓ
degli autoveicoli. L'auto della polizia parte dopo 7,2 s con
accelerazione di 2,0 m/s2. Nell'ipotesi che
l'accelerazione si mantenga costante, calcolare la distanza che
dovrÓ percorrere l'auto della polizia per raggiungere
l'automobile e l'intervallo di tempo impiegato.
[36 s; 1296 m]
72. Un aeroplano mentre vola alla velocitÓ di 300 m/s
accelera con accelerazione costante uguale a 5,00 m/s2
per 4.00 s. Da questo istante continua il suo volo alla velocitÓ
raggiunta. Eseguire un diagramma velocitÓ-tempo per i primi 10,0
s dall'istante in cui inizia ad accelerare. Calcolare inoltre lo
spazio percorso dall'aeroplano dopo i primi 4 s e dopo i primi 10
s.
[1,24 • 103 m; 3,16 • 103 m]
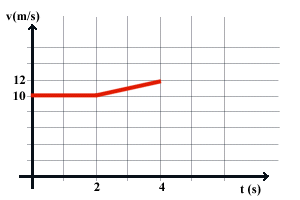
73. II grafico velocitÓ-tempo di un ciclista Ŕ riportato in
figura. Calcolare lo spazio percorso dopo 2,0 s e dopo 4,0 s e la
velocitÓ media nei primi 4,0 s.

[20 m; 42 m; 10,5 m/s]
74. Utilizzando il grafico velocitÓ-tempo del ciclista
dell'esercizio precedente, calcolare l'accelerazione per t = 1 s
e per t = 3 s. Rappresentare il grafico accelerazione-tempo
durante i primi 4 s.
[0; 1 m/s2]
75. Un punto materiale si muove con legge oraria s(t) = 4t2
+ 2t 1 in cui s e t sono espressi rispettivamente in metri e in
secondi. Determinare la legge secondo cui la velocitÓ varia in
funzione del tempo, partendo dalla definizione di velocitÓ
istantanea come limite della velocitÓ media.
Calcolare inoltre la velocitÓ media, utilizzando una
calcolatrice, nell'intervallo di tempo [1 - Dt,
1 + Dt] di centro 1 con Dt = 2; 1; 0,1. In quale relazione sono le
velocitÓ medie cosý calcolate con la velocitÓ istantanea per t
= 1? Ripetere il calcolo della velocitÓ media con Dt? generico ricorrendo al calcolo
letterale.
[v=2 + 8t, ...]
76. La velocitÓ e lo spazio percorso da un punto materiale in moto sopra una retta sono espressi in funzione del tempo dalla tabella qui sotto. Eseguendo opportune rappresentazioni grafiche, determinare la legge tempo-velocitÓ e la legge tempo-spazio ed eseguire una verifica dei risultati ottenuti.
| t(s) | 0 | 4 | 8 | 12 | 16 |
| v(m/s) | 0 | 16 | 32 | 48 | 64 |
| x(m) | 0 | 32 | 128 | 288 | 512 |
[x= 4t; x=2t2]
77. Risolvere l'esercizio precedente nel caso in cui la velocitÓ e lo spazio percorso sono espressi in funzione del tempo dalla tabella sotto.
| t(s) | 0 | 4 | 8 | 12 | 16 |
| v(m/s) | 0 | 40 | 80 | 120 | 160 |
| x(m) | 0 | 80 | 320 | 720 | 1280 |
[x=10t; x = 5t2]
78. Un ciclista pedala alla velocitÓ di 36 km/h; durante gli
ultimi 4 s dello sprint finale aumenta la velocitÓ fino a 50,4
km/h. Calcolare l'accelerazione media e, nell'ipotesi che
l'accelerazione si mantenga costante, lo spazio percorso durante
i 4 s finali.
[1 m/s2; 48 m]
79. Un'automobile viaggia alla velocitÓ di 36 km/h. Premendo
il pedale dell'acceleratore per 10 s la velocitÓ arriva con
accelerazione costante a 108 km/h.
Determinare la pendenza del grafico velocitÓ-tempo e lo spazio
percorso dall'automobile nell'intervallo di tempo considerato.
[2,0 m/s2; 2,0 • 102 m]
80. Un'automobile parte da ferma con accelerazione costante
uguale a 2 m/s2. Calcolare lo spazio percorso
dall'automobile dopo aver raggiunto la velocitÓ di 32 m/s.
[256 m]