
COME CON L'ISTESSE
LINEE POSSIAMO TROVARE LA PROPORZIONE
TRA DUE FIGURE SUPERFICIALI TRA DI LORO SIMILI.
Operazione IX.
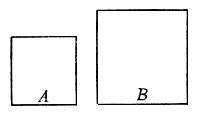 Sianci, per essempio, proposti li due quadrati A, B, o vero
qualunque due altre figure, delle quali le due medesime linee A, B siano
lati omologhi. Volendo trovar qual proporzione abbino tra di loro le dette superficie,
prendasi con un compasso la linea B, la quale, aprendo lo Strumento, si applichi a
qual si voglia punto di esse Linee Geometriche, e sia, per essempio, al 20; dipoi, non
movendo lo Strumento, prendasi col compasso la linea A, e questa applicata alle
Linee Geometriche, veggasi a che numero si adatti; e trovato, v. g., che si aggiusti al
numero 10, dirai la proporzione delle due figure esser quella che ha 20 a 10, cioè
doppia. E quando la grandezza di questa linea non si accomodasse precisamente ad alcuna
delle divisioni, dobbiamo rinovare l'operazione, ed, applicando ad altri punti che alli
20, tentare sin tanto che l'altra linea ancora esattamente si accomodi a qualche punto; il
che trovato, sapremo consequentemente la proporzione delle due figure assegnateci, per
esser lei sempre la medesima che quella de i numeri delli due punti, alli quali le dette
linee, nella medesima apertura dello Strumento, si accomodano. E quando dell'una delle due
piante proposteci fusse data la capacità, si troverà il contenuto dell'altra nel
medesimo modo. Come, per essempio: Essendo la pianta della linea B 30 campi, si
cerca quanto saria la pianta A: accomoda la linea B trasversalmente ai punti
30, e vedi poi a qual numero si adatti, pur trasversalmente, la linea A; e tanti
campi dirai contenere la pianta di essa linea A. Sianci, per essempio, proposti li due quadrati A, B, o vero
qualunque due altre figure, delle quali le due medesime linee A, B siano
lati omologhi. Volendo trovar qual proporzione abbino tra di loro le dette superficie,
prendasi con un compasso la linea B, la quale, aprendo lo Strumento, si applichi a
qual si voglia punto di esse Linee Geometriche, e sia, per essempio, al 20; dipoi, non
movendo lo Strumento, prendasi col compasso la linea A, e questa applicata alle
Linee Geometriche, veggasi a che numero si adatti; e trovato, v. g., che si aggiusti al
numero 10, dirai la proporzione delle due figure esser quella che ha 20 a 10, cioè
doppia. E quando la grandezza di questa linea non si accomodasse precisamente ad alcuna
delle divisioni, dobbiamo rinovare l'operazione, ed, applicando ad altri punti che alli
20, tentare sin tanto che l'altra linea ancora esattamente si accomodi a qualche punto; il
che trovato, sapremo consequentemente la proporzione delle due figure assegnateci, per
esser lei sempre la medesima che quella de i numeri delli due punti, alli quali le dette
linee, nella medesima apertura dello Strumento, si accomodano. E quando dell'una delle due
piante proposteci fusse data la capacità, si troverà il contenuto dell'altra nel
medesimo modo. Come, per essempio: Essendo la pianta della linea B 30 campi, si
cerca quanto saria la pianta A: accomoda la linea B trasversalmente ai punti
30, e vedi poi a qual numero si adatti, pur trasversalmente, la linea A; e tanti
campi dirai contenere la pianta di essa linea A.
Torna alla pagina dell'indice
COME SI POSSA
COSTITUIRE UNA FIGURA SUPERFICIALE
SIMILE ED EGUALE A MOLTE ALTRE SIMILI PROPOSTECI.
Operazione X.
 Sianci, per essempio, proposte tre figure simili, delle quali li
lati omologhi siano le linee A, B, C, alle quali se ne debbe trovar
una sola eguale, e pure ad esse simile. Prendi col compasso la lunghezza della linea C,
e questa, aperto lo Strumento, applicherai a qual numero più ti piace delle Linee
Geometriche, e sia, v. g., applicata alli punti 12.12; dipoi, lasciato lo Strumento in tal
sito, prendi la linea B, e vedi a che numero delle medesime linee si accomodi, che
sia, per essempio, al 9; e perché l'altra si era aggiustata al 12, congiugnerai questi
due numeri 9 e 12 insieme, e terrai a memoria 21; piglia dipoi la terza linea A, e,
secondo il medesimo ordine, considera a qual numero delle medesime linee trasversalmente
si adatti, e trovato, v. g., adattarsi al 6, aggiugnerai 6 al 21, che salvasti, e averai
in tutto 27. Piglia dunque la distanza trasversale tra li punti 27, ed averai la linea D;
sopra la quale facendo una figura simile a le altre 3 proposte, sarà ancora di grandezza
alle medesime tre insieme eguale. E col medesimo ordine ne potrai ridurre in una sola
quante ne venissero proposte, pur che le proposte siano tutte simili tra di loro. Sianci, per essempio, proposte tre figure simili, delle quali li
lati omologhi siano le linee A, B, C, alle quali se ne debbe trovar
una sola eguale, e pure ad esse simile. Prendi col compasso la lunghezza della linea C,
e questa, aperto lo Strumento, applicherai a qual numero più ti piace delle Linee
Geometriche, e sia, v. g., applicata alli punti 12.12; dipoi, lasciato lo Strumento in tal
sito, prendi la linea B, e vedi a che numero delle medesime linee si accomodi, che
sia, per essempio, al 9; e perché l'altra si era aggiustata al 12, congiugnerai questi
due numeri 9 e 12 insieme, e terrai a memoria 21; piglia dipoi la terza linea A, e,
secondo il medesimo ordine, considera a qual numero delle medesime linee trasversalmente
si adatti, e trovato, v. g., adattarsi al 6, aggiugnerai 6 al 21, che salvasti, e averai
in tutto 27. Piglia dunque la distanza trasversale tra li punti 27, ed averai la linea D;
sopra la quale facendo una figura simile a le altre 3 proposte, sarà ancora di grandezza
alle medesime tre insieme eguale. E col medesimo ordine ne potrai ridurre in una sola
quante ne venissero proposte, pur che le proposte siano tutte simili tra di loro.
Torna alla pagina dell'indice
PROPOSTE DUE
FIGURE SIMILI E DISEGUALI, TROVAR LA TERZA
SIMILE ED EGUALE ALLA DIFFERENZA DELLE DUE PROPOSTE.
Operazione XI.
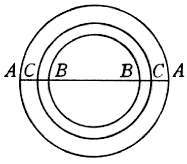 La presente operazione è il converso della già dichiarata nel precedente
capitolo; e la sua operazione sarà in tal guisa. Sianci, per essempio, proposti 2 cerchi
diseguali, e del maggiore sia diametro la linea AA, e del minore la BB:
volendo trovar il semidiametro del cerchio eguale alla differenza delli due A, B,
prendi con un compasso la lunghezza della linea maggiore A, ed applicala, aprendo
lo Strumento, a qual punto più ti piacerà delle Linee Geometriche, e sia, per essempio,
applicata al numero 20; e non movendo lo Strumento, considera a qual punto delle medesime
linee si aggiusta la linea B, e trovato, per essempio, accomodarsi al numero 8,
sottratto questo di 20, resterà 12; e presa la distanza tra li punti 12.12, averai la
linea C, il cui cerchio sarà eguale alla differenza delli due A, B.
E quello che si è assemplificato ne i cerchi per via de i loro semidiametri, intendasi
esser l'istesso nelle altre figure simili, operando con uno de i loro dati omologhi. La presente operazione è il converso della già dichiarata nel precedente
capitolo; e la sua operazione sarà in tal guisa. Sianci, per essempio, proposti 2 cerchi
diseguali, e del maggiore sia diametro la linea AA, e del minore la BB:
volendo trovar il semidiametro del cerchio eguale alla differenza delli due A, B,
prendi con un compasso la lunghezza della linea maggiore A, ed applicala, aprendo
lo Strumento, a qual punto più ti piacerà delle Linee Geometriche, e sia, per essempio,
applicata al numero 20; e non movendo lo Strumento, considera a qual punto delle medesime
linee si aggiusta la linea B, e trovato, per essempio, accomodarsi al numero 8,
sottratto questo di 20, resterà 12; e presa la distanza tra li punti 12.12, averai la
linea C, il cui cerchio sarà eguale alla differenza delli due A, B.
E quello che si è assemplificato ne i cerchi per via de i loro semidiametri, intendasi
esser l'istesso nelle altre figure simili, operando con uno de i loro dati omologhi.
Torna alla pagina dell'indice
ESTRAZIONE DELLA
RADICE QUADRATA CON L'AIUTO DELLE MEDESIME LINEE.
Operazione XII.
Tre differenti modi di operare nell'estrazion della radice quadrata saranno nel
presente capitolo dichiarati, uno per li numeri mediocri, uno per li grandi, ed il terzo
per li piccioli: intendendo per i numeri mediocri quelli che sono, tanto nel meno quanto
nel più, intorno al 5000; maggiori, quelli che sono intorno al 50000; minimi, quelli che
sono intorno al 100. E prima faremo principio da i numeri mediocri.
Per estrar dunque e trovar la radice quadrata di un numero mezano proposto, prima
devesi aggiustar lo Strumento, la qual cosa sarà con l'accomodare trasversalmente al 16
delle Linee Geometriche lo spazio di 40 punti preso rettamente dalle Linee Aritmetiche:
dipoi del numero proposto leva via le due ultime figure, che dinotano le unità e le
decine; e quel numero che resta, prendi trasversalmente dalle Linee Geometriche, e
misuralo rettamente sopra le Aritmetiche; e quello che trovi sarà la radice quadrata del
numero proposto. Come, per essempio, volendo la radice di questo numero 4630, levate le
due ultime figure, cioè il 30, resta 46; però piglierai trasversalmente 46 dalle Linee
Geometriche e lo misurerai rettamente sopra le Aritmetiche, e lo troverai contenere punti
68, che è la prossima radice cercata.
Ma sono in questa regola da notarsi due cose. La prima è, che quando le due ultime
figure, che si levano, passassero 50, devi al numero che resta aggiungere uno: come se,
v.g., volessi pigliare la radice di 4192, perché il 92 da levarsi passa 50, in luogo del
41, che restava, devi prendere 42, e nel resto seguire la regola di sopra.
L'altra cautela, che si deve osservare, è che quando quello che resta, detratte le due
ultime figure, passasse 50, in tal caso, poi che la divisione delle Linee Geometriche non
si estende oltre al 50, si deve del numero che resta prendere la metà o vero altra parte,
e questa distanza presa, si deve geometricamente raddoppiare o secondo il numero della
detta parte multiplicare; e quell'ultimo intervallo così multiplicato, misurato
rettamente sopra le Linee Aritmetiche, ti darà la radice che cerchi. Come, per essempio,
vogliamo la radice di 8412: aggiustato, come è detto, lo Strumento, e detratte le due
ultime figure, resta 84, il qual numero non è sopra le Linee Geometriche; però piglierai
la sua metà, cioè 42: preso dunque lo spazio trasversale tra li punti 42, bisognerà che
geometricamente sia raddoppiato, il che farai con aprir più lo Strumento, sin tanto che
il detto spazio si adatti a qualche numero del quale sopra le medesime linee ve ne sia uno
doppio; come, v. g., saria adattandolo al 20, pigliando poi l'intervallo tra li punti 40,
il quale, misurato finalmente sopra le Linee Aritmetiche, ti mostrerà 91 e due terzi in
circa, prossima radice del numero 8412 proposto. E se ti fusse bisognato del numero dato
pigliare la terza parte, nel triplicarla poi geometricamente, l'applicherai
trasversalmente ad un numero delle Linee Geometriche del quale ve ne sia un altro triplo,
come saria al 10 per pigliare il 30, o al 12 per pigliar il 36.
Quanto al modo di procedere per i numeri maggiori, non si averà altra differenza dal
modo precedente, se non nell'aggiustar lo Strumento e nel levar dal dato numero le tre
ultime note. E l'aggiustar lo Strumento si farà pigliando 100 rettamente dalle Linee
Aritmetiche, aggiustandolo poi trasversalmente alli punti 10.10 delle Geometriche: il che
fatto, volendo, v. g., la radice quadrata di 32140, tolte le tre ultime figure, resta 32,
e questo piglierai trasversalmente dalle Linee Geometriche; che, misurato rettamente sopra
le Aritmetiche, ti mostrerà 179, prossima radice di 32140. Avvertendo che l'istesse
cautele notate nell'operazione precedente si devono per l'appunto osservare in questa:
cioè, che quando le tre figure, che si detraggono, passano 500, si ha da aggiunger uno a
quello che resta; e se quel che resta passa 50, se ne piglierà una parte, cioè la metà
o il terzo, etc., dupplicando o triplicando, al modo dichiarato, quello che averai per la
detta parte preso.
Per li numeri minori, aggiusterai lo Strumento secondo il primo modo, cioè con buttare
40 a 16, pigliando poi trasversalmente dalle Linee Geometriche il numero proposto, senza
levarne figura alcuna; perché, misurando rettamente il detto spazio sopra le Linee
Aritmetiche, troverai la radice cercata in numero intero ed in frazione. Ma nota che le
decine delle Linee Aritmetiche ti debbono servire per unità, e le unità per decimi di
unità: come, per essempio, vogliamo la radice di 30; aggiusta lo Strumento, come è
detto, buttando 40, preso dalle Linee Aritmetiche rettamente, al 16 delle Geometriche
trasversalmente, dalle quali, preso transversalmente la distanza delli punti 30,
misurandola rettamente sopra le Aritmetiche, troverai punti 55, che importano 5 intieri e
5 decimi, cioè 5 e mezo; quanta è la prossima radice di 30. Avvertendo che in questa
regola ancora si devono osservare li avvertimenti e cauzioni nelle altre due regole
insegnate.
Torna alla pagina dell'indice
REGOLA PER LE
ORDINANZE DE GLI ESSERCITI DI FRONTE E FIANCO DISEGUALI.
Operazione XIII.
Per le ordinanze di fronte eguale al fianco ci servirà, come è manifesto,
l'estrarre la radice quadrata del numero de i soldati propostoci. Ma quando volessimo
formare un'ordinanza con una moltitudine assegnata di soldati, della quale la fronte ed il
fianco non fussero eguali, ma si rispondessero in una data proporzione, allora, per
risolvere il quesito, ci bisogna in altra maniera procedere, operando nel modo che nel
seguente essempio si dichiara.
Sendoci dunque ordinato che ritroviamo la fronte ed il fianco di 4335 soldati, messi in
ordinanza in maniera che per ogni cinque, che saranno nella fronte, ne siano tre nel
fianco, allora, per conseguir l'intento con l'aiuto del nostro Strumento, prima,
considerando i numeri della proporzione assegnataci esser 5 e 3, aggiungendo a ciascuno di
loro un 0, fingeremo che importino 50 e 30. E per trovar la fronte, prenderemo rettamente
con un compasso 50 dalle Linee Aritmetiche, e quest'intervallo accomoderemo
trasversalmente alle Linee Geometriche, ed a quel numero che si produce dalla
moltiplicazione tra di loro de i numeri della proporzione assegnata, cioè (nel presente
essempio) al 15; e lasciato lo Strumento in tale stato, si prenderà trasversalmente, pur
nelle medesime Linee Geometriche, la distanza tra li punti segnati dal numero che resta,
detratte le decine ed unità dal numero de i soldati propostoci, che nel presente essempio
è 43; e misurato tale intervallo rettamente sopra le Linee Aritmetiche, ci darà la
fronte di tale ordinanza, che sarà soldati 85. E col medesimo ordine troveremo il fianco,
pigliando rettamente 30 dalle Linee Aritmetiche, e buttandolo trasversalmente al 15 delle
Geometriche, e da esse immediatamente pigliando, pur trasversalmente, l'intervallo tra li
punti 43.43; il quale, misurato rettamente sopra le Linee Aritmetiche, ci darà 51 per il
fianco. Ed il medesimo ordine si terrà in ogni altra moltitudine di soldati, ed in
qualunque altra proporzione assegnataci: avvertendo che, sì come si disse nella radice
quadrata, quando le unità e decine che si levano dal numero proposto passassero 50, si
deve alle centinaia, che restano, aggiugnere uno di più, etc. Né voglio tacere come,
trovata che si sarà la fronte secondo la regola già dichiarata, si potria con altra
regola più spedita, e con le sole Linee Aritmetiche, trovar il fianco, in questa forma
operando. Già nell'essempio addotto fu trovato 85 per la fronte, e furno i numeri della
proporzione 5 e 3, che è quanto se si dicesse 50 e 30, o vero 100 e 60, etc.: però
quello 85, preso rettamente dalle Linee Aritmetiche, accomodisi trasversalmente al 100
delle medesime, e piglisi immediatamente l'intervallo, pur trasversale, tra li punti 60.60
delle medesime linee; il quale, misurato rettamente, ci mostrerà il medesimo numero 51,
che nell'altra maniera di operare fu ritrovato.
E questa operazione, che sotto l'essempio delle ordinanze aviamo dichiarata, intendasi
esser la regola di uno de i capitoli di algebra, cioè de i censi eguali al numero; onde
tutti i quesiti che per esso si risolvono, si scioglieranno anco operando col nostro
Strumento nella maniera già dichiarata.
Torna alla pagina dell'indice
INVENZIONE DELLA
MEDIA PROPORZIONALE PER VIA DELLE MEDESIME LINEE.
Operazione XIV.
 Con
l'aiuto di queste linee e loro divisioni potremo tra due linee, o vero due numeri dati,
trovare con gran facilità la linea o il numero medio proporzionale in questa maniera.
Siano li due numeri, o vero le due linee misurate proposteci, l'uno 36 e l'altro 16: e
presa col compasso la lunghezza dell'una, v. g., della 36, applicala, aprendo lo
Strumento, alli punti 36 delle Linee Geometriche, e non movendo lo Strumento, prendi
l'intervallo tra li punti 16.16 delle medesime linee, il quale, misurato sopra la medesima
scala, troverai esser punti 24; quanto appunto è il numero proporzionale tra 36 e 16. E
nota che, per misurar le linee proposte, potremo servirci non solo della scala notata
sopra lo Strumento, ma di qualunque altra ancora, quando quella dello Strumento fusse
troppo piccola per il nostro bisogno. Con
l'aiuto di queste linee e loro divisioni potremo tra due linee, o vero due numeri dati,
trovare con gran facilità la linea o il numero medio proporzionale in questa maniera.
Siano li due numeri, o vero le due linee misurate proposteci, l'uno 36 e l'altro 16: e
presa col compasso la lunghezza dell'una, v. g., della 36, applicala, aprendo lo
Strumento, alli punti 36 delle Linee Geometriche, e non movendo lo Strumento, prendi
l'intervallo tra li punti 16.16 delle medesime linee, il quale, misurato sopra la medesima
scala, troverai esser punti 24; quanto appunto è il numero proporzionale tra 36 e 16. E
nota che, per misurar le linee proposte, potremo servirci non solo della scala notata
sopra lo Strumento, ma di qualunque altra ancora, quando quella dello Strumento fusse
troppo piccola per il nostro bisogno.
Notando in oltre, che quando le linee, ed i numeri che le misurano, tra li quali
vogliamo trovare il medio proporzionale, fussero assai grandi, sì che passassero il 50,
che è il maggiore numero notato sopra le nostre Linee Geometriche, si potrà nondimeno
conseguir l'intento, operando con parti de i proposti numeri, o con altri minori di essi,
ma che abbino la medesima proporzione che hanno li primi; e la regola sarà in questo
modo. Vogliamo, verbi gratia, pigliare il numero medio proporzionale fra 144 ed 81,
li quali eccedono ambidue il cinquanta. Piglisi dalle Linee Aritmetiche 144 rettamente per
applicarlo trasversalmente alle Linee Geometriche; ma perché in esse non vi è numero
così grande, piglierò imaginariamente una parte di esso numero 144, come saria, v. g.,
il terzo, cioè 48, e l'intervallo già preso applicherò trasversalmente alli punti 48
delle Linee Geometriche. Dipoi, imaginata la terza parte di 81, che fu l'altro numero
dato, la quale è 27, piglierò tal numero pur trasversalmente dalle medesime Linee
Geometriche, e questo, misurato rettamente sopra le Aritmetiche, mi darà il medio
proporzionale ricercato, cioè 108.
Torna alla pagina dell'indice
DELLE LINEE STEREOMETRICHE;
E PRIMA COME COL MEZO DI ESSE SI POSSIN CRESCERE O DIMINUIRE
TUTTI LI CORPI SOLIDI SIMILI SECONDO LA DATA PROPORZIONE.
Operazione XV.
 Sono le presenti Linee Stereometriche così dette per esser la lor divisione
secondo la proporzione de i corpi solidi, sino a 148; e da esse trarremo molti usi: il
primo de i quali sarà il già proposto, cioè come, dato un lato di qual si voglia corpo
solido, si possa trovare il lato d'un altro, che ad esso abbia una data proporzione. Come,
per essempio, sia la linea A diametro, v. g., d'una sfera, o palla, per dirlo più
vulgarmente, o vero lato d'un cubo o altro solido, e siaci proposto di dover trovar il
diametro, o lato d'un altro, che a quello abbia la proporzione che ha 20 a 36: piglia col
compasso la linea A, ed aprendo lo Strumento, applicala al punto 36 delle Linee
Stereometriche; il che fatto, prendi immediatamente l'intervallo tra li punti 20.20, che
sarà la linea B, diametro o lato del solido, all'altro, il cui lato A,
nella proporzione data di 20 a 36. Sono le presenti Linee Stereometriche così dette per esser la lor divisione
secondo la proporzione de i corpi solidi, sino a 148; e da esse trarremo molti usi: il
primo de i quali sarà il già proposto, cioè come, dato un lato di qual si voglia corpo
solido, si possa trovare il lato d'un altro, che ad esso abbia una data proporzione. Come,
per essempio, sia la linea A diametro, v. g., d'una sfera, o palla, per dirlo più
vulgarmente, o vero lato d'un cubo o altro solido, e siaci proposto di dover trovar il
diametro, o lato d'un altro, che a quello abbia la proporzione che ha 20 a 36: piglia col
compasso la linea A, ed aprendo lo Strumento, applicala al punto 36 delle Linee
Stereometriche; il che fatto, prendi immediatamente l'intervallo tra li punti 20.20, che
sarà la linea B, diametro o lato del solido, all'altro, il cui lato A,
nella proporzione data di 20 a 36.
Torna alla pagina dell'indice
PROPOSTI DUE
SOLIDI SIMILI, TROVARE QUAL PROPORZIONE ABBINO FRA DI LORO.
Operazione XVI.
 Non è la presente operazione molto differente dalle dichiarate di sopra,
e puossi con gran facilità risolvere. Quando dunque ci venissero proposte le due linee A,
B, e dimandato qual proporzione abbino fra di loro i lor solidi simili, prenderemo
una di esse col compasso; e sia, v. g., presa l'A, la quale applicheremo, aprendo
lo Strumento, a qualche numero delle presenti linee, e sia applicata, v. g., al 50.50; e
subito presa la lunghezza dell'altra linea B, veggasi a qual numero si accomodi; e
trovato adattarsi, per essempio, al 21, diremo il solido A al solido B avere
la proporzione di 50 a 21. Non è la presente operazione molto differente dalle dichiarate di sopra,
e puossi con gran facilità risolvere. Quando dunque ci venissero proposte le due linee A,
B, e dimandato qual proporzione abbino fra di loro i lor solidi simili, prenderemo
una di esse col compasso; e sia, v. g., presa l'A, la quale applicheremo, aprendo
lo Strumento, a qualche numero delle presenti linee, e sia applicata, v. g., al 50.50; e
subito presa la lunghezza dell'altra linea B, veggasi a qual numero si accomodi; e
trovato adattarsi, per essempio, al 21, diremo il solido A al solido B avere
la proporzione di 50 a 21.
Torna alla pagina dell'indice
PROPOSTI SOLIDI
SIMILI QUANTI NE PIACERÀ,
TROVARNE UN SOLO EGUALE A TUTTI QUELLI.
Operazione XVII.
 Siano proposte le tre linee A, B, C, lati di
tre solidi simili; vogliamo trovarne uno eguale a tutti quelli. Per il che fare, prendasi
con un compasso la linea A, quale s'applichi a qualche punto delle Linee
Stereometriche, e sia, per essempio, al punto 30: e non movendo lo Strumento, considera a
qual numero s'adatti la linea B, e trovato, per essempio, adattarsi al 12, aggiugni
questo numero al numero 30 già detto, fa 42; il qual numero terrai a memoria: presa dipoi
con un compasso la linea C, considera a qual numero delle medesime linee
s'accomodi, e sia, per essempio, al 6, e congiunto questo numero con l'altro 42, averemo
48: sì che pigliando l'intervallo tra li punti 48.48, sarà trovata la linea D, il
cui solido sarà eguale alli tre proposti A, B, C. Siano proposte le tre linee A, B, C, lati di
tre solidi simili; vogliamo trovarne uno eguale a tutti quelli. Per il che fare, prendasi
con un compasso la linea A, quale s'applichi a qualche punto delle Linee
Stereometriche, e sia, per essempio, al punto 30: e non movendo lo Strumento, considera a
qual numero s'adatti la linea B, e trovato, per essempio, adattarsi al 12, aggiugni
questo numero al numero 30 già detto, fa 42; il qual numero terrai a memoria: presa dipoi
con un compasso la linea C, considera a qual numero delle medesime linee
s'accomodi, e sia, per essempio, al 6, e congiunto questo numero con l'altro 42, averemo
48: sì che pigliando l'intervallo tra li punti 48.48, sarà trovata la linea D, il
cui solido sarà eguale alli tre proposti A, B, C.
Torna alla pagina dell'indice
ESTRAZIONE DELLA
RADICE CUBA.
Operazione XVIII.
Due modi differenti dichiareremo per l'investigazione della radice cuba di
qualunque proposto numero.
Il primo ci servirà per i numeri mediocri, e l'altro per i massimi; intendendo per
numeri mediocri quelli, da i quali tratte le unità, decine e centinaia, li numeri che
restano non eccedono il 148. Per l'estrazione della radice cuba de i quali, prima
s'aggiusterà lo Strumento, con l'applicare trasversalmente alli punti 64 delle Linee
Stereometriche il 40 preso rettamente dalle Linee Aritmetiche: e fatto questo, leva le 3
ultime note dal numero proposto, e piglia quel che resta dalle Linee Stereometriche
trasversalmente, e misuralo rettamente sopra le Aritmetiche, e quello che trovi sarà la
radice cuba del numero proposto. Come, v. g., cerchiamo la radice cuba di 80216:
aggiustato, come s'è detto, lo Strumento, e tolte via le tre ultime note, resta 80;
piglia dunque trasversalmente 80 dalle Linee Stereometriche, e misuralo rettamente sopra
le Aritmetiche, e troverai 43; quanta è la radice prossima del dato numero. E nota, che
quando, detratte le tre ultime note, restasse più di 148, che è il maggior numero delle
Stereometriche, allora potrai operare per parti. Come, per essempio, si cerca la radice
cuba di 185840: e perché, detratte le ultime 3 note 840, resta 186 (dico 186, ben che
resti 185, perché le centinaia delle tre note detratte sono più di 5, cioè più di mezo
migliaio, onde, pigliandolo per un migliaio intero, fo che quel che resta sia 186, cioè
uno di più), che eccede il 148, piglieremo la sua metà, cioè 93, trasversalmente dalle
Stereometriche già aggiustate; e questo spazio preso si doverà stereometricamente
duplicare, cioè applicarlo a qualche numero delle medesime Stereometriche
trasversalmente, del qual ne sia uno doppio; e questo, preso pur trasversalmente, e
misuratolo sopra la scala Aritmetica, sarà la radice che si cercava. Stando dunque
nell'essempio proposto, applicheremo lo spazio, tra li punti 93 già preso, v. g., al 40
delle Linee Stereometriche, pigliando poi l'80, che, misurato sopra le Linee Aritmetiche,
ci mostrerà 57; ch'è la prossima radice del numero proposto.
L'altro modo di operare per li numeri massimi sarà con aggiustare lo Strumento
applicando la distanza di 100 punti, presa rettamente dalle Linee Aritmetiche, al 100
delle Stereometriche trasversalmente; e sarà aggiustato. Dipoi dal proposto numero devi
levare le quattro ultime note, ed il numero che resta prendere trasversalmente da esse
Linee Stereometriche, e misurarlo rettamente sopra le Aritmetiche: come, per essempio,
sendoci proposto il numero 1404988, avendo già aggiustato lo Strumento al modo detto, e
detratte le quattro ultime note, resta 140; il qual numero, preso trasversalmente dalle
Linee Stereometriche, e misurato rettamente sopra l'Aritmetiche, ci darà 112, radice
prossima del numero proposto. Non ci scordando, che quando le tre note rimanenti
importassero più di 148, numero maggiore delle nostre linee, si deve operare per parti,
come nell'altra regola superiore fu avvertito.
Torna alla pagina dell'indice
INVENZIONE DELLE
DUE MEDIE PROPORZIONALI.
Operazione XIX.
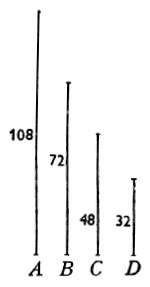 Quando
ci fussero proposti due numeri, o due linee misurate, tra le quali dovessimo trovare due
altre medie proporzionali, potremo ciò esseguire facilmente col mezo delle presenti
linee; e ciò con questo essempio si farà chiaro. Quando
ci fussero proposti due numeri, o due linee misurate, tra le quali dovessimo trovare due
altre medie proporzionali, potremo ciò esseguire facilmente col mezo delle presenti
linee; e ciò con questo essempio si farà chiaro.
Dove ci vengono proposte le due linee A, D, delle quali l'una sia, per
essempio, 108 e l'altra 32: e presa la maggiore con un compasso, adattisi, aperto lo
Strumento, alli numeri 108.108; e poi prendasi l'intervallo tra li punti 32.32, il quale
sarà la lunghezza della seconda linea B, che, misurata con la medesima scala con
la quale furono misurate le proposte linee, si troverà esser 72; e per trovarne la terza
linea C, adattisi pure di nuovo, sopra le medesime Linee Stereometriche, la linea B
alli punti 108.108, e tornisi di nuovo a pigliare la distanza tra li punti 32.32, che tale
sarà la grandezza della terza linea C; e misurata sopra la medesima scala, si
troverà essere punti 48. E notisi che non è necessario il prender prima la maggior linea
più che la minore; ma nell'uno e nell'altro modo operando, sempre si troverà l'istesso.
Torna alla pagina dell'indice
COME OGNI SOLIDO
PARALLELEPIPEDO SI POSSA COL MEZO DELLE LINEE STEREOMETRICHE RIDURRE IN CUBO.
Operazione XX.
Siaci proposto il solido parallelepipedo, le cui dimensioni siano diseguali, cioè
72, 32 e 84: cercasi il lato del cubo ad esso eguale. Piglia il medio proporzionale fra 72
e 32, nel modo dichiarato di sopra nell'operazione XIV, cioè piglia 72 rettamente dalla
scala Aritmetica, e buttalo trasversalmente al 72 delle Linee Geometriche; ma perché non
vanno tant'oltre, buttalo alla metà, cioè al 36: e subito prendi pur trasversalmente
l'altro numero dalle medesime linee, cioè 32; anzi pur, per dir meglio, piglia la sua
metà, cioè il 16 (avendo buttato il primo 72 alla sua metà parimente); e questo che
troverai, sarà, come è manifesto, il numero medio proporzionale tra 72 e 32: misuralo
dunque sopra le Linee Aritmetiche, e lo troverai esser 48; onde lo butterai
trasversalmente a questo medesimo numero 48 delle Linee Stereometriche; e senza muovere
poi lo Strumento, prendi pur trasversalmente il terzo numero del solido proposto, cioè
l'84, e sarà finita l'operazione, perché facendo questa tal linea lato di un Cubo,
quello sarà veramente eguale al solido proposto; e misurandola sopra la scala Aritmetica,
la troverai esser 57 e mezo in circa.
Torna alla pagina dell'indice
|