 |
Galileo Galilei
Intorno alle cose che stanno in su l'acqua o che in quella si muovonoSettima pagina |
Ma non è già che qual si voglia gran mole, che galleggi nell'acqua stagnante, non
possa esser mossa da qualunque minima forza, e solo è vero che minor forza più
lentamente la muove: ma quando la resistenza dell'acqua all'esser divisa fosse in alcun
modo sensibile, converrebbe che detta mole a qualche sensibil forza restasse al tutto
immobile; il che non avviene. Anzi dirò di più, che, quando noi ci ritirassimo a più
interna contemplazione della natura dell'acqua e de gli altri fluidi, forse scorgeremmo,
la costituzione delle parti loro esser tale che non solamente non contrasti alla
divisione, ma che niente vi sia che a divider s'abbia; sì che la resistenza che si sente
nel muoversi per l'acqua, sia simile a quella che proviamo nel caminar avanti per una gran
calca di persone, dove sentiamo impedimento, e non per difficoltà che si abbia nel
dividere, non si dividendo alcuno di quelli onde la calca è composta, ma solamente nel
muover lateralmente le persone, già divise non congiunte; e così proviamo resistenzia
nel cacciare un legno in un monte di rena, non perché parte alcuna della rena si abbia a
segare, ma solamente a muovere e sollevare. Due maniere pertanto, di penetrare ci si
rappresentano: una ne i corpi le cui parti fosser continue, e qui par necessaria la
divisione; l'altra negli aggregati di parti non continue, ma contigue solamente, e qui non
fu bisogno di dividere, ma di muover solamente. Ora, io non son ben resoluto se l'acqua e
gli altri fluidi si devono stimar di parti continue, o contigue solamente. Sento ben
inclinarmi al crederle più presto contigue (quando non sia in natura altra maniera di
aggregare che con l'unione o col toccamento de gli estremi), e a ciò m'induce il veder
gran differenza tra la copula delle parti di un corpo duro, e la copula delle medesime
parti quando l'istesso corpo sarà fatto liquido e fluido: perché, se, per esemplo, io
piglierò una massa d'argento o altro metallo freddo e duro, sentirò, nel dividerlo in
due parti, non solo la resistenza che si sentirebbe al muoverle solamente, ma un'altra
incomparabilmente maggiore, dependente da quella virtù, qualunque ella sia, che le tiene
attaccate; e così, se vorremo dividere ancora e dette due parti in altre due, e
successivamente in altre e altre, troverremo continuamente simili resistenze, ma sempre
minori quanto più le parti da dividersi saranno piccole; ma quando finalmente, adoprando
sottilissimi e acutissimi strumenti, quali sono le più tenui parti del fuoco, lo
solveremo forse nell'ultime e minime sue particelle, non resterà in loro più non solo la
resistenza alla divisione, ma né anco il poter più esser divise, e massime da strumenti
più grossi de gli aculei del fuoco. E qual sega o coltello, che si metta nell'argento ben
fuso, troverà da dividere cosa che sia avanzata al partimento del fuoco? certo nissuna,
perché o 'l tutto sarà già stato ridotto alle sottilissime e ultime divisioni, o, se
pure vi restassero parti capaci ancora di altre suddivisioni, non potriano riceverle se
non da divisori più acuti del fuoco; ma tale non è un'assicella o una verga di ferro,
che si movesse per il metallo fuso. Di costituzione e positura simile stimo esser le parti
dell'acqua e de gli altri fluidi, cioè incapaci di esser divise per la lor tenuità, o,
se pur non in tutto indivisibili, al meno certo non divisibili da una tavola o da altro
corpo solido trattabile dalle nostre mani, dovendo la sega esser più sottile del solido
da segarsi. Muovono dunque solamente, e non dividono, i corpi solidi che si pongono
nell'acqua; le cui parti, essendo già divise sino a i minimi e perciò potendo esserne
mosse molte insieme e poche e pochissime, dan subito luogo ad ogni piccolo corpuscolo che
in esse descenda, perché, per minimo e leggiero che sia, scendendo nell'aria e arrivando
alla superficie dell'acqua trova particelle di acqua più piccole e di resistenza minore
all'esser mosse e scacciate, che non è la forza sua propria premente e scacciante, onde
e' si tuffa e ne muove quella porzione che è proporzionata alla sua possanza. Non è
dunque resistenza alcuna nell'acqua all'esser divisa, anzi non vi son parti che a divider
s'abbino. Soggiungo appresso che, quando pure vi si trovasse qualche minima resistenza (il
che assolutamente è falsissimo), forse nel voler con un capello muover una grandissima
macchina natante, o nel voler con la giunta di un minimo grano di piombo far descendere al
fondo, o con la suttrazzione far salire alla superficie, una gran falda di materia
similissima in gravità all'acqua (il che parimente non accaderà quando si operi
destramente); notisi che una cotal resistenza è cosa diversissima da quella che gli
avversarii producono per causa del galleggiar le falde di piombo o l'assicelle d'ebano;
perché si potrà fare una tavola d'ebano, che posata su l'acqua galleggi, né sia
bastante anco la giunta di cento grani di piombo, posativi sopra, a sommergerla, che poi,
bagnata, non solo descenderà levati i detti piombi, ma non basteranno alcuni suveri o
altri corpi leggieri attaccatigli a ritenerla dallo scender sino al fondo. Or veggasi se,
dato anco che nella sustanza dell'acqua si trovasse qualche minima resistenza alla
divisione, questa ha che far nulla con quella causa che sostien l'assicella sopra l'acqua,
con resistenza centomila volte maggiore di quella che altri potesse ritrovar nelle parti
dell'acqua. Né mi si dica che la superficie solamente dell'acqua ha tal resistenza, ma
non le parti interne, o veramente che tal resistenza si trova grandissima nel cominciare a
fendere, come anco par che nel cominciare il moto si trovi maggior contrasto che nel
continuarlo: perché, prima, io permetterò che l'acqua si agiti e si confondano le parti
supreme con le medie e con l'infime, o vero che si levino totalmente via quelle di sopra e
si adoprino quelle di mezo; e tuttavia si vedrà far l'effetto stesso: di più, quel
capello che tira una trave per l'acqua ha pur a divider le parti supreme, ed ha anco a
cominciare il moto; e pur lo comincia, e pur le divide: e, finalmente, mettasi l'assicella
a mezz'acqua, e quivi si tenga sospesa un pezzo e ferma, e poi lascisi in libertà, che
ella subito comincerà il moto e lo continuerà sino al fondo; ma, di più, la tavoletta
quando si ferma sopra l'acqua, ha già non pur cominciato a muoversi ed a dividere, ma per
buono spazio si è affondata.
Ricevasi, dunque, per vera e indubitata conclusione, che l'acqua non ha renitenza
alcuna alla semplice divisione, e che non è possibile il ritrovar corpo solido alcuno, di
qualunque figura esser si voglia, al quale, messo nell'acqua, resti dalla crassizie di
quella proibito e tolto il muoversi in su o in giù, secondoché egli supererà o sarà
superato dall'acqua in gravità, ancorché l'eccesso e differenza sia insensibile. Quando,
dunque, noi vediamo la falda d'ebano, o d'altra materia più grave dell'acqua, trattenersi
a' confini dell'acqua e dell'aria senza sommergersi, ad altro fonte bisogna che
ricorriamo, per investigar la cagion di cotale effetto, che alla larghezza della figura
impotente a superar la renitenza con la quale l'acqua contrasta alla divisione, già che
tal resistenza non è, e da quello che non è non si dee attendere azione alcuna. Resta,
dunque, come già s'è detto, verissimo, ciò avvenire perché quello che si posa in tal
modo su l'acqua, non è il medesimo corpo che quello che si mette nell'acqua: perché
questo, che si mette nell'acqua, è la pura falda d'ebano, che, per esser più grave
dell'acqua, va al fondo; e quello che si posa su l'acqua, è un composto d'ebano e di
tanta aria, che tra ambedue sono in ispecie men gravi dell'acqua, e però non discendono.
Confermo ancor più questo ch'io dico. Già, signori avversari, noi convegniamo che la
gravità del solido, maggiore o minore della gravità dell'acqua, è vera e propriissima
cagione dell'andare o non andare al fondo. Ora, se voi volete mostrare che, oltre alla
detta cagion, ce ne sia un'altra, la qual sia così potente che possa impedire e rimuovere
l'andare al fondo a quei solidi medesimi che per loro gravità vi vanno, e questa dite che
è l'ampiezza della figura, voi siete in obbligo, qualunque volta vogliate mostrare una
tale esperienza, di render prima i circustanti sicuri, che quel solido, che voi ponete
nell'acqua, non sia men grave in ispecie di lei; perché, quando voi ciò non faceste,
ciascuno potrebbe con ragion dire che non la figura, ma la leggerezza, fosse cagion di tal
galleggiare. Ma io vi dico che, quando voi mostrate di metter nell'acqua l'assicella
d'ebano, non vi ponete altramente un solido più grave in ispecie dell'acqua, ma un più
leggiere; perché, oltr'all'ebano, è in acqua una mole d'aria, unita con l'assicella,
tanta e così leggiera, che d'amendue si fa un composto men grave dell'acqua: rimovete per
tanto l'aria, e ponete nell'acqua l'ebano solo, ché così vi porrete un solido più grave
dell'acqua; e se questo non andrà in fondo, voi bene avrete filosofato, e io male.
Ora, poi ch'e' s'è ritrovata la vera cagion del galleggiar di quei corpi, che per
altro, come più gravi dell'acqua, dovrieno discendere in fondo, parmi che, per intera e
distinta cognizion di questa materia, sia bene l'andar dimostrativamente scoprendo quei
particolari accidenti che accaggiono intorno a cotali effetti, investigando quali
proporzioni debbano aver diverse figure di differenti materie con la gravità dell'acqua,
per potere, in virtù dell'aria contigua, sostenersi a galla.
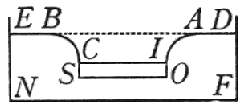 Sia,
dunque, per chiara intelligenza, il vaso DFNE, nel quale sia contenuta l'acqua; e
sia una lamina, o tavoletta, la cui grossezza venga compresa tra le linee IC, OS,
e sia di materia più grave dell'acqua, sì che, posta su l'acqua, s'avvalli e abbassi
sotto il livello di essa acqua, lasciando gli arginetti AI, BC, li quali
sien della massima altezza che esser possano; in modo che se la lamina IS
s'abbassasse ancora per qualsivoglia minimo spazio, gli arginetti non più consistessero,
ma, scacciando l'aria AICB, si diffondessero sopra la superficie IC e
sommergessero la lamina. È dunque l'altezza AI, BC la massima profondità
che ammettono gli arginetti dell'acqua. Ora io dico che da questa e dalla proporzione che
avrà in gravità la materia della lamina all'acqua, noi potremo agevolmente ritrovar di
quanta grossezza, al più, si possano fare le dette lamine, acciò si sostengano su
l'acqua. Imperocché, se la materia della lamina IS sarà, v. g., il doppio più
grave dell'acqua, una lamina di tal materia potrà esser grossa, al più, quanto è
l'altezza massima degli argini, cioè quanto è l'altezza AI. Il che dimostrerremo
così. Sia il solido IS di gravità doppia alla gravità dell'acqua, e sia o prisma
o cilindro retto, cioè che abbia le due superficie piane, superiore e inferiore, simili
ed eguali e a squadra con l'altre superficie laterali, e sia la sua grossezza IO
eguale all'altezza massima degli argini dell'acqua: dico che, posto su l'acqua, non si
sommergerà. Imperocché, essendo l'altezza AI eguale all'altezza IO, sarà
la mole dell'aria ABCI eguale alla mole del solido CIOS, e tutta la mole AOSB
doppia della mole IS: e avvegnaché la mole dell'aria AC non cresca o
diminuisca la gravità della mole IS, e 'l solido IS si pone doppio in
gravità all'acqua, adunque tant'acqua quanta è la mole sommersa AOSB, composta
dell'aria AICB e del solido IOSC, pesa appunto quanto essa mole sommersa AOSB:
ma quando tanta mole d'acqua, quanta è la parte sommersa del solido, pesa quanto lo
stesso solido, esso non discende più, ma si ferma, come da Archimede, e sopra da noi, è
stato dimostrato: adunque IS non discenderà più, ma si fermerà. E se il solido IS
sarà in gravità sesquialtero all'acqua, resterà a galla, sempre che la sua grossezza
non sia più che 'l doppio dell'altezza massima dell'argine, cioè di AI.
Imperocché, essendo IS sesquialtero in gravità all'acqua, ed essendo l'altezza OI
doppia della IA, sarà ancora il solido sommerso AOSB sesquialtero in mole
al solido IS: e perché l'aria AC non cresce o scema il peso del solido IS,
adunque tanta acqua, quanta è la mole sommersa AOSB, pesa quanto essa mole
sommersa: adunque tal mole si fermerà. E in somma, universalmente, ogni volta che
l'eccesso della gravità del solido sopra la gravità dell'acqua, alla gravità dell'acqua
avrà la medesima proporzione che l'altezza dell'arginetto alla grossezza del solido, tal
solido non andrà al fondo; ma d'ogni maggior grossezza, andrebbe. Sia,
dunque, per chiara intelligenza, il vaso DFNE, nel quale sia contenuta l'acqua; e
sia una lamina, o tavoletta, la cui grossezza venga compresa tra le linee IC, OS,
e sia di materia più grave dell'acqua, sì che, posta su l'acqua, s'avvalli e abbassi
sotto il livello di essa acqua, lasciando gli arginetti AI, BC, li quali
sien della massima altezza che esser possano; in modo che se la lamina IS
s'abbassasse ancora per qualsivoglia minimo spazio, gli arginetti non più consistessero,
ma, scacciando l'aria AICB, si diffondessero sopra la superficie IC e
sommergessero la lamina. È dunque l'altezza AI, BC la massima profondità
che ammettono gli arginetti dell'acqua. Ora io dico che da questa e dalla proporzione che
avrà in gravità la materia della lamina all'acqua, noi potremo agevolmente ritrovar di
quanta grossezza, al più, si possano fare le dette lamine, acciò si sostengano su
l'acqua. Imperocché, se la materia della lamina IS sarà, v. g., il doppio più
grave dell'acqua, una lamina di tal materia potrà esser grossa, al più, quanto è
l'altezza massima degli argini, cioè quanto è l'altezza AI. Il che dimostrerremo
così. Sia il solido IS di gravità doppia alla gravità dell'acqua, e sia o prisma
o cilindro retto, cioè che abbia le due superficie piane, superiore e inferiore, simili
ed eguali e a squadra con l'altre superficie laterali, e sia la sua grossezza IO
eguale all'altezza massima degli argini dell'acqua: dico che, posto su l'acqua, non si
sommergerà. Imperocché, essendo l'altezza AI eguale all'altezza IO, sarà
la mole dell'aria ABCI eguale alla mole del solido CIOS, e tutta la mole AOSB
doppia della mole IS: e avvegnaché la mole dell'aria AC non cresca o
diminuisca la gravità della mole IS, e 'l solido IS si pone doppio in
gravità all'acqua, adunque tant'acqua quanta è la mole sommersa AOSB, composta
dell'aria AICB e del solido IOSC, pesa appunto quanto essa mole sommersa AOSB:
ma quando tanta mole d'acqua, quanta è la parte sommersa del solido, pesa quanto lo
stesso solido, esso non discende più, ma si ferma, come da Archimede, e sopra da noi, è
stato dimostrato: adunque IS non discenderà più, ma si fermerà. E se il solido IS
sarà in gravità sesquialtero all'acqua, resterà a galla, sempre che la sua grossezza
non sia più che 'l doppio dell'altezza massima dell'argine, cioè di AI.
Imperocché, essendo IS sesquialtero in gravità all'acqua, ed essendo l'altezza OI
doppia della IA, sarà ancora il solido sommerso AOSB sesquialtero in mole
al solido IS: e perché l'aria AC non cresce o scema il peso del solido IS,
adunque tanta acqua, quanta è la mole sommersa AOSB, pesa quanto essa mole
sommersa: adunque tal mole si fermerà. E in somma, universalmente, ogni volta che
l'eccesso della gravità del solido sopra la gravità dell'acqua, alla gravità dell'acqua
avrà la medesima proporzione che l'altezza dell'arginetto alla grossezza del solido, tal
solido non andrà al fondo; ma d'ogni maggior grossezza, andrebbe.
Sia il solido IS più grave dell'acqua, e di grossezza tale che tal proporzione
abbia l'altezza dell'argine AI alla grossezza del solido IO, quale ha
l'eccesso della gravità di esso solido IS sopra la gravità d'una mole d'acqua
eguale alla mole IS, alla gravità della mole d'acqua eguale alla mole IS:
dico che il solido IS non si sommergerà; ma d'ogni maggior grossezza, andrà al
fondo. Imperocché, essendo come AI ad IO, così l'eccesso della gravità
del solido IS sopra la gravità d'una mole d'acqua eguale alla mole IS, alla
gravità della medesima mole d'acqua, sarà, componendo, come AO ad OI così
la gravità del solido IS alla gravità d'una mole d'acqua eguale alla mole IS,
e, convertendo, come IO ad OA così la gravità d'una mole d'acqua eguale
alla mole IS alla gravità del solido IS: ma come IO ad OA,
così una mole d'acqua IS ad una mole d'acqua eguale alla mole ABSO, e la
gravità d'una mole d'acqua IS alla gravità d'una mole d'acqua AS: adunque
come la gravità d'una mole d'acqua eguale alla mole IS alla gravità del solido IS,
così la medesima gravità d'una mole d'acqua IS alla gravità d'una mole d'acqua AS.
Adunque la gravità del solido IS è eguale alla gravità d'una mole d'acqua eguale
alla mole AS: ma la gravità del solido IS è la medesima che la gravità
del solido AS, composto del solido IS e dell'aria ABCI: adunque tanto
pesa tutto il solido composto AOSB, quanto pesa l'acqua che si conterrebbe nel
luogo di esso composto AOSB; e però si farà l'equilibrio e la quiete, né più si
profonderà esso solido IOSC. Ma se la sua grossezza IO si crescesse,
bisognerebbe crescere ancora l'altezza dell'argine AI per mantener la debita
proporzione: ma, per lo supposto, l'altezza dell'argine AI è la massima che la
natura dell'acqua e dell'aria permettano, senza che l'acqua scacci l'aria aderente alla
superficie del solido IC e ingombri lo spazio AICB: adunque solido di
maggior grossezza che IO, e della medesima materia del solido IS, non
resterà senza sommergersi, ma discenderà al fondo: che è quello che bisognava
dimostrare.
In conseguenza di questo che s'è dimostrato, molte e varie conclusioni si posson
raccorre, dalle quali più e più sempre venga confermata la verità della mia principal
proposizione, e scoperto quanto imperfettamente sia stato sin ora filosofato circa la
presente quistione.
E prima, raccogliesi dalle cose dimostrate, che tutte le materie, ancorché gravissime,
possono sostenersi su l'acqua, sino allo stesso oro, grave più d'ogni altro corpo
conosciuto da noi: perché, considerata la sua gravità esser quasi venti volte maggior di
quella dell'acqua, e, più, determinata l'altezza massima dell'argine che può far l'acqua
senza rompere il ritegno dell'aria aderente alla superficie del solido che si posa su
l'acqua, se noi faremo una lamina d'oro così sottile che non ecceda in grossezza la
diciannovesima parte dell'altezza del detto arginetto, questa, posata leggiermente su
l'acqua, resterà senza andare in fondo. E se l'ebano, per caso, sarà in proporzione
sesquisettima più grave dell'acqua, la massima grossezza che si possa dare ad una
tavoletta d'ebano, sì che ella possa sostenersi senza sommergersi, sarà sette volte più
che l'altezza dell'arginetto. Lo stagno, v. g., otto volte più grave dell'acqua,
galleggerà ogni volta che la grossezza della sua lamina non ecceda la settima parte
dell'altezza dell'arginetto.
E già non voglio passar sotto silenzio di notare, come un secondo corollario
dependente dalle cose dimostrate, che l'ampiezza della figura non solamente non è cagion
del galleggiar quei corpi gravi che per altro si sommergono, ma né anche da lei depende
il determinare quali sieno quelle falde d'ebano, di ferro o d'oro che possano stare a
galla; anzi tal determinazione dalla sola grossezza di esse figure d'ebano o d'oro si dee
attendere, escludendo totalmente la considerazione della lunghezza e della larghezza, come
quelle che in verun conto non hanno parte in questo effetto. Già si è fatto manifesto,
come cagione del galleggiare le dette falde ne è solamente il ridursi ad esser men gravi
dell'acqua, mercé dell'accoppiamento di quell'aria che insieme con loro discende e occupa
luogo nell'acqua; il qual luogo occupato se, avanti che l'acqua circunfusa si sparga ad
ingombrarlo, sarà capace di tant'acqua che pesasse quanto la falda, resta la falda
sospesa su l'acqua, né più si sommerge. Or veggasi da quale delle tre dimensioni del
solido dependa il determinare quale e quanta debba esser la mole di quello, acciocché
l'aiuto dell'aria, che se le accoppierà, possa esser bastante a renderlo men grave in
ispecie dell'acqua, ond'egli resti senza sommergersi: troverrassi senz'alcun dubbio che la
lunghezza o larghezza non hanno che fare in simil determinazione, ma solamente l'altezza o
vogliam dir la grossezza. Imperocché, se si piglierà una falda o tavoletta, per esemplo,
d'ebano, la cui altezza alla massima possibile altezza dell'arginetto abbia la proporzione
dichiarata di sopra, il perché ella soprannuoti sì, ma non già se s'accresce punto la
sua grossezza, dico che, servata la sua grossezza, e crescendo due quattro e dieci volte
la sua superficie, o scemandola col dividerla in quattro o sei o venti e cento parti,
sempre resterà nel medesimo modo a galla; ma se si crescerà solo un capello la sua
grossezza, sempre si profonderà, quando bene la superficie si multiplicasse per cento e
cento volte. Ora, conciossiacosa che quella sia cagione, la qual posta, si pon l'effetto,
e tolta, si toglie, e per crescere o diminuire in qualunque modo la larghezza e lunghezza
non si pone o rimuove l'effetto d'andare o non andare al fondo; adunque l'ampiezza o
picciolezza della superficie non hanno azione alcuna circa l'andare o non andare al fondo.
E che, posta la proporzione dell'altezza dell'argine all'altezza del solido nel modo di
sopra detto, la grandezza o piccolezza della superficie non faccia variazione alcuna, è
manifesto da quello che di sopra si è dimostrato, e da questo: che i prismi e i cilindri
che hanno la medesima base, son fra di loro come l'altezze; onde i cilindri o prismi,
cioè le tavolette, grandi o piccole ch'elle sieno, pur che tutte sien d'egual grossezza,
hanno la medesima proporzione all'aria sua conterminale, che ha per base la medesima
superficie della tavoletta e per altezza l'arginetto dell'acqua; sì che sempre di tale
aria e della tavoletta si compongono solidi, che in gravità pareggiano una mole d'acqua
eguale alla mole di essi solidi, composti dell'aria e della tavoletta: per lo che tutti i
detti solidi restano nel medesimo modo a galla.
Raccoglieremo, nel terzo luogo, come ogni sorta di figura e di qualsivoglia materia,
benché più grave dell'acqua, può, per beneficio dell'arginetto, non solamente
sostenersi senza andare al fondo, ma alcune figure, benché di materia gravissima, restare
anche tutte sopra l'acqua, non si bagnando se non la superficie inferiore che tocca
l'acqua; e queste saranno tutte le figure le quali dalla base inferiore in su si vanno
assottigliando: il che noi esemplificheremo per ora nelle piramidi o coni, delle quali
figure le passioni son comuni. Dimostreremo dunque, come è possibile formare una piramide
o cono di qualsivoglia materia proposta, il quale, posato con la base sopra l'acqua, resti
non solo senza sommergersi, ma senza bagnarsi altro che la base. Per la cui esplicazione
fa di bisogno prima dimostrare il seguente lemma, cioè che:
I solidi de' quali le moli in proporzione rispondono contrariamente alle lor gravità
in ispecie, son di gravità assoluta eguali.
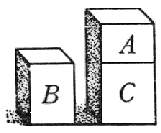 Sieno
due solidi, AC e B; e sia la mole AC alla mole B come la
gravità in ispecie del solido B alla gravità in ispecie del solido AC:
dico, i solidi AC e B esser di peso assoluto eguali, cioè egualmente gravi.
Imperocché, se la mole AC sia eguale alla mole B, sarà, per l'assunto, la
gravità in ispecie di B eguale alla gravità in ispecie di AC; ed essendo
eguali in mole e della medesima gravità in ispecie, peseranno anche assolutamente tanto
l'uno come l'altro. Ma se le lor moli saranno diseguali, sia la mole AC maggiore,
ed in essa prendasi la parte C eguale alla mole B; e perché le moli B,
C sono eguali, la medesima proporzione avrà il peso assoluto di B al peso
assoluto di C, che ha la gravità in ispecie di B alla gravità in ispecie
di C, o vero di CA, che in ispecie è la medesima: ma qual proporzione ha la
gravità in ispecie di B alla gravità in ispecie di CA, tale, per lo dato,
ha la mole AC alla mole B, cioè alla mole C: adunque il peso
assoluto di B al peso assoluto di C è come la mole AC alla mole C.
Ma come la mole AC alla mole C, così è il peso assoluto di AC al
peso assoluto di C: adunque il peso assoluto di B al peso assoluto di C
ha la medesima proporzione che 'l peso assoluto di AC al medesimo peso assoluto di C:
adunque i due solidi AC e B pesano di peso assoluto egualmente: che è
quello che bisognava dimostrare. Sieno
due solidi, AC e B; e sia la mole AC alla mole B come la
gravità in ispecie del solido B alla gravità in ispecie del solido AC:
dico, i solidi AC e B esser di peso assoluto eguali, cioè egualmente gravi.
Imperocché, se la mole AC sia eguale alla mole B, sarà, per l'assunto, la
gravità in ispecie di B eguale alla gravità in ispecie di AC; ed essendo
eguali in mole e della medesima gravità in ispecie, peseranno anche assolutamente tanto
l'uno come l'altro. Ma se le lor moli saranno diseguali, sia la mole AC maggiore,
ed in essa prendasi la parte C eguale alla mole B; e perché le moli B,
C sono eguali, la medesima proporzione avrà il peso assoluto di B al peso
assoluto di C, che ha la gravità in ispecie di B alla gravità in ispecie
di C, o vero di CA, che in ispecie è la medesima: ma qual proporzione ha la
gravità in ispecie di B alla gravità in ispecie di CA, tale, per lo dato,
ha la mole AC alla mole B, cioè alla mole C: adunque il peso
assoluto di B al peso assoluto di C è come la mole AC alla mole C.
Ma come la mole AC alla mole C, così è il peso assoluto di AC al
peso assoluto di C: adunque il peso assoluto di B al peso assoluto di C
ha la medesima proporzione che 'l peso assoluto di AC al medesimo peso assoluto di C:
adunque i due solidi AC e B pesano di peso assoluto egualmente: che è
quello che bisognava dimostrare.
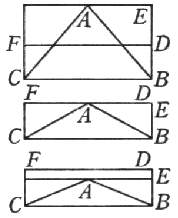 Avendo
dimostrato questo, dico che è possibile di qual si voglia materia proposta formare una
piramide o cono, sopra qualsivoglia base, il quale, posato su l'acqua, non si sommerga né
bagni, altro che la base. Sia la massima possibile altezza dell'argine la linea DB;
e 'l diametro della base del cono da farsi, di qualunque materia assegnata, sia la linea BC,
ad angolo retto con DB; e la proporzione che ha la gravità in ispecie della
materia della piramide o cono da farsi, alla gravità in ispecie dell'acqua, la medesima
abbia l'altezza dell'argine DB alla terza parte dell'altezza della piramide o cono ABC,
fatto su la base il cui diametro sia BC: dico che detto cono ABC, e ogni
altro più basso di lui, resterà sopra la superficie dell'acqua BC senza
sommergersi. Tirisi la DF parallela alla BC, e intendasi il prisma o
cilindro EC, il quale sarà triplo al cono ABC: e perché il cilindro DC
al cilindro CE ha la medesima proporzione che l'altezza DB all'altezza BE,
ma il cilindro CE al cono ABC è come l'altezza EB alla terza parte
dell'altezza del cono, adunque, per la proporzione eguale, il cilindro DC al cono ABC
è come DB alla terza parte dell'altezza BE. Ma come DB alla terza
parte di BE, così è la gravità in ispecie del cono ABC alla gravità in
ispecie dell'acqua: adunque, come la mole del solido DC alla mole del cono ABC,
così la gravità in ispecie di esso cono alla gravità in ispecie dell'acqua: adunque,
per lo lemma precedente, il cono ABC pesa assolutamente come una mole d'acqua
eguale alla mole DC. Ma l'acqua che per la 'mposizione del cono ABC viene
scacciata del suo luogo, è quanta capirebbe precisamente nel luogo DC, ed è in
peso eguale al cono che la scaccia: adunque si farà l'equilibrio, e 'l cono resterà
senza più profondarsi. Ed è manifesto, che faccendosi sopra la medesima base un cono
meno alto, sarà anche men grave, e tanto più resterà senza sommergersi. Avendo
dimostrato questo, dico che è possibile di qual si voglia materia proposta formare una
piramide o cono, sopra qualsivoglia base, il quale, posato su l'acqua, non si sommerga né
bagni, altro che la base. Sia la massima possibile altezza dell'argine la linea DB;
e 'l diametro della base del cono da farsi, di qualunque materia assegnata, sia la linea BC,
ad angolo retto con DB; e la proporzione che ha la gravità in ispecie della
materia della piramide o cono da farsi, alla gravità in ispecie dell'acqua, la medesima
abbia l'altezza dell'argine DB alla terza parte dell'altezza della piramide o cono ABC,
fatto su la base il cui diametro sia BC: dico che detto cono ABC, e ogni
altro più basso di lui, resterà sopra la superficie dell'acqua BC senza
sommergersi. Tirisi la DF parallela alla BC, e intendasi il prisma o
cilindro EC, il quale sarà triplo al cono ABC: e perché il cilindro DC
al cilindro CE ha la medesima proporzione che l'altezza DB all'altezza BE,
ma il cilindro CE al cono ABC è come l'altezza EB alla terza parte
dell'altezza del cono, adunque, per la proporzione eguale, il cilindro DC al cono ABC
è come DB alla terza parte dell'altezza BE. Ma come DB alla terza
parte di BE, così è la gravità in ispecie del cono ABC alla gravità in
ispecie dell'acqua: adunque, come la mole del solido DC alla mole del cono ABC,
così la gravità in ispecie di esso cono alla gravità in ispecie dell'acqua: adunque,
per lo lemma precedente, il cono ABC pesa assolutamente come una mole d'acqua
eguale alla mole DC. Ma l'acqua che per la 'mposizione del cono ABC viene
scacciata del suo luogo, è quanta capirebbe precisamente nel luogo DC, ed è in
peso eguale al cono che la scaccia: adunque si farà l'equilibrio, e 'l cono resterà
senza più profondarsi. Ed è manifesto, che faccendosi sopra la medesima base un cono
meno alto, sarà anche men grave, e tanto più resterà senza sommergersi.
È manifesto ancora, come si possono far coni e piramidi di qualsivoglia materia più
grave dell'acqua, li quali, posti nell'acqua con la sommità o punta in giù, restino
senza andare in fondo. Perché, se ripiglieremo quello che di sopra fu dimostrato de'
prismi e cilindri, e che in base eguali a quelle di essi cilindri formeremo coni della
medesima materia e tre volte più alti de' cilindri, quelli resteranno a galla; perché
saranno in mole e peso eguali ad essi cilindri, e, per aver le lor base eguali a quelle
de' cilindri, lasceranno sopra eguali moli d'aria contenuta dentro gli arginetti.
Questo, che per modo d'esemplo s'è dimostrato de' prismi, cilindri coni e piramidi, si
potrebbe dimostrare di tutte l'altre figure solide; ma bisognerebbe, tanta è la
moltitudine e la varietà de' lor sintomi e accidenti, formarne un volume intero, volendo
comprendere le particolari dimostrazioni di tutti e de' loro segmenti. Ma voglio, per non
estendere il presente discorso in infinito, contentarmi che da quanto ho dichiarato ogni
uno di mediocre intelligenza possa comprendere, come non è materia alcuna così grave,
insino all'oro stesso, della quale non si possano formar tutte le sorte di figure, le
quali, in virtù dell'aria superiore ad esse aderente, e non per resistenza dell'acqua
alla penetrazione, restino sostenute, sì che non discendano al fondo: anzi di più
mostrerò, per rimuovere un tale errore, come una piramide o cono, posto nell'acqua con la
punta in giù, resterà senza andare a fondo, e 'l medesimo, posto con la base in giù,
andrà in fondo, e sarà impossibile il farlo soprannotare; e pur tutto l'opposito accader
dovrebbe, se la difficultà del fender l'acqua fusse quella che impedisse la scesa,
conciosiacosa che il medesimo cono è molto più accomodato a fendere e penetrare con la
punta acutissima che con la base larga e spaziosa.
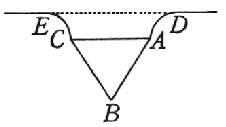 E
sia, per dimostrar questo, il cono ABC, due volte grave quanto l'acqua, e sia la
sua altezza tripla all'altezza dell'arginetto DAEC: dico, primieramente, che, posto
nell'acqua leggiermente con la punta in giù, non discenderà al fondo. Imperocché il
cilindro aereo, contenuto tra gli argini DA, CE, in mole è eguale al cono ABC,
tal che tutta la mole del solido composto dell'aria DACE e del cono ABC
sarà doppia del cono ACB: e perché il cono ABC si pone di materia il
doppio più grave dell'acqua, adunque tant'acqua quant'è tutta la mole DABCE,
locata sotto 'l livello dell'acqua, pesa quanto il cono ABC, e però si farà
l'equilibrio; e 'l cono ABC non calerà più a basso. E
sia, per dimostrar questo, il cono ABC, due volte grave quanto l'acqua, e sia la
sua altezza tripla all'altezza dell'arginetto DAEC: dico, primieramente, che, posto
nell'acqua leggiermente con la punta in giù, non discenderà al fondo. Imperocché il
cilindro aereo, contenuto tra gli argini DA, CE, in mole è eguale al cono ABC,
tal che tutta la mole del solido composto dell'aria DACE e del cono ABC
sarà doppia del cono ACB: e perché il cono ABC si pone di materia il
doppio più grave dell'acqua, adunque tant'acqua quant'è tutta la mole DABCE,
locata sotto 'l livello dell'acqua, pesa quanto il cono ABC, e però si farà
l'equilibrio; e 'l cono ABC non calerà più a basso.
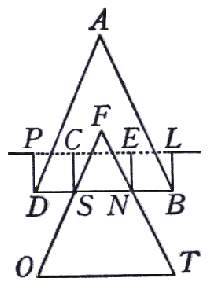 Dico
ora, di più, che 'l medesimo cono, posato con la base all'ingiù, calerà al fondo, ed
essere impossibile che egli in modo alcuno resti a galla. Sia dunque il cono ABD,
doppio in gravità all'acqua, e sia la sua altezza tripla dell'altezza dell'argine LB.
È già manifesto che tutto fuori dell'acqua non resterà: perché, essendo il cilindro
compreso dentro agli argini LB, DP eguale al cono ABD, ed essendo la
materia del cono doppia in gravità all'acqua, è manifesto che il peso di esso cono sarà
doppio al peso della mole d'acqua eguale al cilindro LBDP; adunque non resterà in
questo stato, ma discenderà. Dico, in oltre, che molto meno si fermerà sommergendone una
parte: il che s'intenderà comparando con l'acqua tanto la parte che si sommergerà,
quanto l'altra che avanzerà fuori. Sommergasi, dunque, del cono ABD la parte NTOS,
e avanzi la punta NSF: sarà l'altezza del cono FNS o più che la metà di
tutta l'altezza del cono FTO, o vero non sarà più. Se sarà più che la metà, il
cono FNS sarà più che la metà del cilindro ENSC; imperocché l'altezza
del cono FNS sarà più che sesquialtera dell'altezza del cilindro ENSC: e
perché si pone che la materia del cono sia in ispecie il doppio più grave dell'acqua,
l'acqua che si conterrebbe dentro all'arginetto ENSC sarebbe assolutamente men
grave del cono FNS: onde il cono solo FNS non può esser sostenuto
dall'arginetto. Ma la parte sommersa NTOS, per essere in ispecie più grave il
doppio dell'acqua, tenderà al fondo: adunque tutto il cono FTO, tanto rispetto
alla parte sommersa, quanto all'eminente, discenderà al fondo. Ma se l'altezza della
punta FNS sarà la metà di tutta l'altezza del cono FTO, sarà la medesima
altezza di esso cono FNS sesquialtera all'altezza EN; e però ENSC
sarà doppio del cono FNS, e tanta acqua in mole quanto è il cilindro ENSC,
peserebbe quanto la parte del cono FNS. Ma perché l'altra parte sommersa NTOS
è in gravità doppia all'acqua, tanta mole d'acqua quanta è quella che si compone del
cilindro ENSC e del solido NTOS peserà manco del cono FTO tanto,
quanto è il peso d'una mole d'acqua eguale al solido NTOS: adunque il cono
discenderà ancora. Dico
ora, di più, che 'l medesimo cono, posato con la base all'ingiù, calerà al fondo, ed
essere impossibile che egli in modo alcuno resti a galla. Sia dunque il cono ABD,
doppio in gravità all'acqua, e sia la sua altezza tripla dell'altezza dell'argine LB.
È già manifesto che tutto fuori dell'acqua non resterà: perché, essendo il cilindro
compreso dentro agli argini LB, DP eguale al cono ABD, ed essendo la
materia del cono doppia in gravità all'acqua, è manifesto che il peso di esso cono sarà
doppio al peso della mole d'acqua eguale al cilindro LBDP; adunque non resterà in
questo stato, ma discenderà. Dico, in oltre, che molto meno si fermerà sommergendone una
parte: il che s'intenderà comparando con l'acqua tanto la parte che si sommergerà,
quanto l'altra che avanzerà fuori. Sommergasi, dunque, del cono ABD la parte NTOS,
e avanzi la punta NSF: sarà l'altezza del cono FNS o più che la metà di
tutta l'altezza del cono FTO, o vero non sarà più. Se sarà più che la metà, il
cono FNS sarà più che la metà del cilindro ENSC; imperocché l'altezza
del cono FNS sarà più che sesquialtera dell'altezza del cilindro ENSC: e
perché si pone che la materia del cono sia in ispecie il doppio più grave dell'acqua,
l'acqua che si conterrebbe dentro all'arginetto ENSC sarebbe assolutamente men
grave del cono FNS: onde il cono solo FNS non può esser sostenuto
dall'arginetto. Ma la parte sommersa NTOS, per essere in ispecie più grave il
doppio dell'acqua, tenderà al fondo: adunque tutto il cono FTO, tanto rispetto
alla parte sommersa, quanto all'eminente, discenderà al fondo. Ma se l'altezza della
punta FNS sarà la metà di tutta l'altezza del cono FTO, sarà la medesima
altezza di esso cono FNS sesquialtera all'altezza EN; e però ENSC
sarà doppio del cono FNS, e tanta acqua in mole quanto è il cilindro ENSC,
peserebbe quanto la parte del cono FNS. Ma perché l'altra parte sommersa NTOS
è in gravità doppia all'acqua, tanta mole d'acqua quanta è quella che si compone del
cilindro ENSC e del solido NTOS peserà manco del cono FTO tanto,
quanto è il peso d'una mole d'acqua eguale al solido NTOS: adunque il cono
discenderà ancora.
Anzi, perché il solido NTOS è settuplo al cono FNS, del quale il
cilindro ES è doppio, sarà la proporzione del solido NTOS al cilindro ENSC
come di 7 a 2: adunque tutto il solido composto del cilindro ENSC e del solido NTOS
è molto meno che doppio del solido NTOS: adunque il solido solo NTOS è
molto più grave che una mole d'acqua eguale al composto del cilindro ENSC e NTOS:
dal che ne segue che, quando anche si rimovesse e togliesse via la parte del cono FNS,
il restante solo NTOS andrebbe al fondo. E se più si profonderà il cono FTO,
tanto più sarà impossibile che si sostenga a galla, crescendo sempre la parte sommersa NTOS
e scemando la mole dell'aria contenuta dentro all'arginetto, il quale si fa sempre minore
quanto più il cono si sommerge.
Tal cono, dunque, che con la base in su e la cuspide in giù si sostiene senza andare
al fondo, posto con la base in giù è impossibile che non si sommerga. Lungi dal vero,
adunque, hanno filosofato coloro che hanno attribuito la cagion del soprannotare alla
resistenza dell'acqua in esser divisa come a principio passivo, e alla larghezza della
figura di chi l'ha da dividere, come efficiente.
Vengo, nel quarto luogo, a raccogliere e concludere la ragione di quello che io proposi
agli avversari, cioè: Che è possibile formar corpi solidi di qual si voglia figura e di
qual si voglia grandezza, li quali per sua natura vadano a fondo, ma con l'aiuto dell'aria
contenuta nell'arginetto restino senza sommergersi.
La verità di questa proposizione è assai manifesta in tutte quelle figure solide le
quali terminano nella lor più alta parte in una superficie piana; perché, formandosi
tali figure di qualche materia grave in ispecie come l'acqua, mettendole nell'acqua sì
che tutta la mole si ricuopra, è manifesto che si fermeranno in tutti i luoghi, dato
però che tal maniera di peso eguale all'acqua si potesse a capello aggiustare, e
resteranno anche, in conseguenza, al pelo dell'acqua, senza farsi arginetto alcuno. Se
dunque, rispetto alla materia, tali figure sono atte a restare senza sommergersi, benché
prive dell'aiuto dell'arginetto, chiara cosa è ch'elle si potranno far tanto crescer di
gravezza, senza crescer la lor mole, quanto è il peso di tanta acqua, quanta si
conterrebbe dentro all'arginetto che si facesse intorno alla loro piana superficie
superiore; dal cui aiuto sostenute, resteranno a galla; ma bagnate andranno al fondo,
essendo state fatte più gravi dell'acqua. Nelle figure, dunque, che terminano di sopra in
un piano, chiaramente si comprende come l'arginetto, posto o tolto, può vietare o
permettere la scesa: ma in quelle che si vanno verso la sommità attenuando, potrà
qualcuno, e non senza molta apparente cagione, dubitare se queste possano far lo stesso, e
massimamente quelle che vanno a terminare in una acutissima punta, come sono i coni e le
piramidi sottili. Di queste, dunque, come più dubbie di tutte l'altre, cercherò di
dimostrare come esse ancora soggiacciono al medesimo accidente d'andare e non andare al
fondo le medesime, e sieno di qual si voglia grandezza.
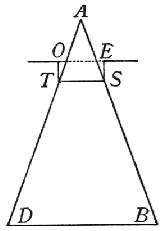 Sia
dunque il cono ABD, fatto di materia grave in ispecie come l'acqua: è manifesto
che, messo tutto sott'acqua, resterà in tutti i luoghi (intendasi sempre quando
esquisitissimamente pesasse quanto l'acqua, il che è quasi impossibile a effettuarsi), e
che ogni piccola gravità che se gli aggiunga, andrà al fondo. Ma se si calerà a basso
leggiermente, dico che si farà l'arginetto ESTO, e che resterà fuori dell'acqua
la punta AST, d'altezza tripla all'altezza dell'argine ES. Il che si fa
manifesto: imperocché, pesando la materia del cono egualmente come l'acqua, la parte
sommersa SBDT resta indifferente al muoversi in giù o in su; e 'l cono AST
essendo eguale in mole all'acqua che si conterrebbe dentro all'arginetto ESTO, gli
sarà anche eguale in gravità; e però sarà in tutto fatto l'equilibrio e, in
conseguenza, la quiete. Sia
dunque il cono ABD, fatto di materia grave in ispecie come l'acqua: è manifesto
che, messo tutto sott'acqua, resterà in tutti i luoghi (intendasi sempre quando
esquisitissimamente pesasse quanto l'acqua, il che è quasi impossibile a effettuarsi), e
che ogni piccola gravità che se gli aggiunga, andrà al fondo. Ma se si calerà a basso
leggiermente, dico che si farà l'arginetto ESTO, e che resterà fuori dell'acqua
la punta AST, d'altezza tripla all'altezza dell'argine ES. Il che si fa
manifesto: imperocché, pesando la materia del cono egualmente come l'acqua, la parte
sommersa SBDT resta indifferente al muoversi in giù o in su; e 'l cono AST
essendo eguale in mole all'acqua che si conterrebbe dentro all'arginetto ESTO, gli
sarà anche eguale in gravità; e però sarà in tutto fatto l'equilibrio e, in
conseguenza, la quiete.
Nasce ora il dubbio, se si possa far più grave il cono ABD tanto, che quando
sia messo tutto sott'acqua vada al fondo, ma non già tanto che si levi all'arginetto la
facultà del poter sostenerlo senza sommergersi. E la ragione del dubitare è questa: che
se bene, quando il cono ABD è in ispecie grave come l'acqua, l'arginetto ESTO
lo sostiene non solamente quando la punta AST è tripla in altezza all'altezza
dell'argine ES, ma più ancora quando minor parte ne restasse fuori dell'acqua
(perché se bene, nel discender che fa il cono, la punta AST scema, e scema
altresì l'arginetto ESTO, nientedimeno con maggior proporzione scema la punta che
l'argine; la quale si diminuisce secondo tutte e tre le dimensioni, ma l'argine secondo
due solamente, restando sempre l'altezza la medesima; o vogliam dire perché il cono ST
va scemando secondo la proporzione de' cubi delle linee che di mano in mano si fanno
diametri delle base de' coni emergenti, e gli arginetti scemando secondo la proporzion de'
quadrati delle medesime linee, onde le proporzioni delle punte son sempre sesquialtere
delle proporzioni de' cilindri contenuti dentro agli arginetti: onde se, per esemplo,
l'altezza della punta emergente fosse doppia o eguale all'altezza dell'argine, in questi
casi il cilindro contenuto dentro all'argine sarebbe assai maggiore della detta punta,
perché sarebbe o sesquialtero o triplo; il perché ci avanzerebbe forza per sostener
tutto il cono, già che la parte sommersa non graverebbe più niente); tuttavia, quando
venga aggiunta alcuna gravità a tutta la mole del cono, sì che anche la parte sommersa
non resti senza qualche eccesso di gravità sopra la gravità dell'acqua, non resta chiaro
se 'l cilindro contenuto dentr'all'arginetto, nel calar che farà il cono, potrà ridursi
a tal proporzione con la punta emergente e a tale eccesso di mole sopra la mole di essa,
che possa ristorar l'eccesso della gravità in ispecie del cono sopra la gravità
dell'acqua. E la dubitazione procede perché, se bene, nell'abbassarsi che fa il cono, la
punta emergente AST si diminuisce, per la qual cosa scema ancora l'eccesso della
gravità del cono sopra la gravità dell'acqua, il punto sta che l'argine ancora si
ristrigne, e 'l cilindro contenuto da esso si diminuisce. Tutta via si dimostrerrà come,
essendo il cono ABD di qual si voglia grandezza, e fatto in prima di materia in
gravità similissima all'acqua, se gli possa aggiugner qualche peso, per lo quale e' possa
discendere al fondo quando sia posto sott'acqua, e possa anche, in virtù dell'arginetto,
fermarsi senza sommergersi.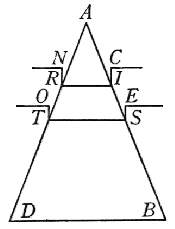
Sia dunque il cono ABD di qualsivoglia grandezza e di gravità simile in ispezie
all'acqua: è manifesto che, messo leggiermente nell'acqua, resterà senza sommergersi, e
fuor dell'acqua avanzerà la punta AST, d'altezza tripla all'altezza dell'argine ES.
Intendasi ora essere il cono ABD abbassato più, sì che avanzi solamente fuor
dell'acqua la punta AIR, alta per la metà della punta AST, con l'arginetto
attorno CIRN. E perché il cono AST al cono AIR è come il cubo della
linea ST al cubo della linea IR; ma il cilindro ESTO al cilindro CIRN
è come il quadrato di ST al quadrato IR; sarà il cono AST ottuplo
al cono AIR, e 'l cilindro ESTO quadruplo al cilindro CIRN: ma il
cono AST è eguale al cilindro ESTO: adunque il cilindro CIRN sarà
doppio al cono AIR, e l'acqua, che si conterrebbe dentro all'arginetto CIRN,
doppia in mole e in peso al cono AIR, e però potente a sostenere il doppio del
peso del cono AIR. Adunque, se a tutto 'l cono ABD s'accrescerà tanto peso
quanto è la gravità del cono AIR, cioè quant'è l'ottava parte del peso del cono
AST, potrà bene ancora esser sostenuto dall'arginetto CIRN; ma senza quello
andrà al fondo, essendosi, per l'aggiunta del peso eguale all'ottava parte del peso del
cono AST, reso il cono ABD più grave in ispecie dell'acqua. Ma se l'altezza
del cono AIR fusse due terzi dell'altezza del cono AST, sarebbe il cono AST
al cono AIR come 27 a 8, e 'l cilindro ESTO al cilindro CIRN come 9 a
4, cioè come 27 a 12, e però il cilindro CIRN al cono AIR come 12 a 8, e
l'eccesso del cilindro CIRN sopra 'l cono AIR al cono AST come 4 a
27: adunque se al cono ABD s'aggiugnerà tanta gravità quant'è li 4
ventisettesimi del peso del cono AST, che è un poco più della sua settima parte,
resterà ancora a galla, e l'altezza della emergente sarà doppia dell'altezza
dell'arginetto. Questo, che s'è dimostrato ne' coni, accade precisamente nelle piramidi,
ancor che e gli uni e l'altre fossero acutissime: dal che si conclude, che il medesimo
accidente accadrà tanto più agevolmente in tutte l'altre figure, quanto in meno acute
sommità vanno a terminare, venendo aiutate da argini più spaziosi.
Tutte le figure adunque, di qualunque grandezza, possono andare e non andare al fondo,
secondo che le lor sommità si bagneranno o non si bagneranno: ed essendo questo accidente
comune a tutte le sorte di figure, senza eccettuarne pur una, adunque la figura non ha
parte alcuna nella produzion di quest'effetto, dell'andare alcuna volta al fondo e
alcun'altra no, ma solamente l'essere ora congiunte con l'aria sopreminente e ora
separate. La qual cagione, in fine, chi rettamente e, come si dice, con amendue gli occhi
considererà questo negozio, conoscerà che si riduce, anzi che realmente è la stessa
vera naturale e primaria cagione del soprannotare o andare al fondo, cioè l'eccesso o
mancamento della gravità dell'acqua verso la gravità di quella mole corporea che si
mette nell'acqua. Perché, sì come una falda di piombo grossa come una costola di
coltello, che per sé sola messa nell'acqua, va al fondo, se sopra se le n'attaccherà una
di suvero grossa quattro dita, resta a galla, perché ora il solido che si pone in acqua
non è altramente, come prima, più grave dell'acqua, ma meno; così la tavoletta d'ebano,
per sua natura più grave dell'acqua, e però discendente in fondo quando per sé sola sia
posta in acqua, se si poserà sopra l'acqua congiunta con un suolo d'aria, la quale
insieme con l'ebano vada abbassandosi, e che sia tanta che con quello faccia un composto
men grave di tanta acqua in mole quanta è la mole già abbassata e sommersa sotto il
livello della superficie dell'acqua, non andrà altramente, ma si fermerà, non per altra
cagione che per la universale e comunissima, che è che le moli corporee men gravi in
ispecie che l'acqua non vanno al fondo. Onde, chi pigliasse una piastra di piombo, grossa,
per esemplo, un dito e larga un palmo per ogni verso, e tentasse di farla restare a galla
col posarla leggiermente, perderebbe ogni fatica, perché, quando si fosse profondata un
capello più che la possibile altezza degli arginetti dell'acqua, si ricoprirebbe e
profonderebbe: ma se, mentre che ella si va abbassando, alcuno le andasse fabbricando
intorno intorno alcune sponde che ritenessero lo spargimento dell'acqua sopra essa
piastra, le quali sponde si alzassero tanto, che dentro di loro potesse capir tant'acqua
che pesasse quanto la detta piastra, ella, senza alcun dubbio, non si profonderebbe più,
ma resterebbe sostenuta in virtù dell'aria contenuta dentro alle già dette sponde; ed in
somma si sarebbe formato un vaso col fondo di piombo. Ma se la sottigliezza del piombo
sarà tale, che pochissima altezza di sponde bastasse per circondar tant'aria che potesse
mantenerlo a galla, e' resterà anche senza le sponde, ma non già senza l'aria; perché
l'aria da per sé stessa si fa sponde, bastanti, per piccola altezza, a ritener lo
'ngombramento dell'acqua; onde quello che 'n questo caso galleggia, è pure un vaso
ripieno d'aria, in virtù della quale resta senza sommergersi.
Voglio, per ultimo, con un'altra esperienza tentar di rimuovere ogni difficultà, se
pur restasse ancora, appresso qualcuno, dubbio circa l'operazione di questa continuazion
dell'aria con la sottil falda che galleggia, e poi por fine a questa parte del mio
Discorso.
Io mi fingo d'essere in questione con alcuno degli avversarii, se la figura abbia
azione alcuna circa l'accrescere o diminuire la resistenza in alcun peso all'essere alzato
nell'aria; e pongo di voler sostener la parte affermativa, affermando che una mole di
piombo, ridotto in figura d'una palla, con manco forza s'alzerà che se il medesimo fusse
fatto in una sottilissima e larghissima falda, come quello che in questa figura spaziosa
ha da fender gran quantità d'aria, e in quella più ristretta e raccolta, pochissima. E
per mostrar come tal mio parer sia vero, sospendo da un sottil filo, prima, la palla, e
quella pongo nell'acqua, legando il filo, che la regge, ad uno de' bracci della bilancia,
la quale tengo in aria, e all'altra lance vo aggiugnendo tanto peso, che finalmente
sollevi la palla del piombo e l'estragga fuor dell'acqua; per che fare vi bisognano, v.
g., 30 once di peso: riduco poi il medesimo piombo in una falda piana e sottile, la qual
pongo parimente nell'acqua, sospesa con 3 fili, li quali la sostengano parallela alla
superficie dell'acqua; e aggiugnendo, nello stesso modo, pesi nell'altra lance, sin che la
falda venga alzata ed estratta fuori dell'acqua, mostro che once 36 non son bastanti di
separarla dall'acqua e sollevarla per aria: e sopra tale esperienza fondato, affermo
d'aver pienamente dimostrata la verità della mia proposizione. Si fa l'avversario innanzi
e, faccendomi abbassare alquanto la testa, mi fa veder cosa della quale io non m'era prima
accorto, e mi mostra che, nell'uscir che fa la falda fuor dell'acqua, ella si tira dietro
un'altra falda d'acqua, la quale, avanti che si divida e separi dalla inferior superficie
della falda di piombo, si eleva sopra il livello dell'altr'acqua più che una costola di
coltello: torna poi a rifar l'esperienza con la palla, e mi fa veder che pochissima
quantità d'acqua è quella che s'attacca alla sua figura stretta e raccolta: mi soggiugne
poi, che non è maraviglia se nel separar la sottile e larghissima falda dall'acqua si
senta molto maggior resistenza che nel separar la palla, poiché insieme con la falda si
ha da alzar gran quantità d'acqua, il che non accade nella palla. Fammi, oltr'a ciò,
avvertito, come la nostra quistione è, se la resistenza all'esser sollevato si ritrova
maggiore in una spaziosa falda di piombo che in una palla, e non se più resista una falda
di piombo con gran quantità d'acqua che una palla con pochissima acqua. Mostrami, in
fine, che il por prima la falda e la palla in acqua, per far prova poi delle loro
resistenze in aria, è fuor del caso nostro, li quali trattiamo del sollevare in aria e
cose locate in aria, e non della resistenza che si fa ne' confini dell'aria e dell'acqua e
da cose che sieno parte in aria e parte in acqua; e finalmente mi fa toccar con mano, che
quando la sottil falda è in aria e libera dal peso dell'acqua, con la stessa forza a
capello si solleva che la palla. Io, vedute e intese queste cose, non so che altro fare se
non chiamarmi persuaso, e ringraziar l'amico d'avermi fatto capace di quello di che per
l'addietro non mi era accorto; e da tale accidente avvertito, dire a gli avversarii, che
la nostra quistione è, se egualmente vada al fondo nell'acqua una palla e una tavola
d'ebano, e non una palla d'ebano e una tavola d'ebano congiunta con un'altra tavola
d'aria; e, più, che noi parliamo dell'andare o non andare al fondo nell'acqua, e non di
quello che accaggia ne' confini dell'acqua e dell'aria a' corpi che sieno parte in aria e
parte in acqua; né meno trattiamo della maggiore o minor forza che si ricerchi nel
separar questo o quel corpo dall'aria; non tacendo loro, in ultimo, che tanto per appunto
resiste e, per così dire, pesa l'aria all'in giù nell'acqua, quanto pesi e resista
nell'acqua all'in su nell'aria, e che la stessa fatica ci vuole a mandar sott'acqua un
utre pien d'aria che ad alzarlo in aria pien d'acqua, rimossa però la considerazion del
peso della pelle e considerando l'acqua e l'aria solamente. E, parimente, è vero che la
stessa fatica si ricerca per mandare, spignendo a basso, un bicchiere e simil vaso sotto
l'acqua, mentre è pieno d'aria, che a sollevarlo sopra la superficie dell'acqua,
tenendolo con la bocca in giù, mentre egli sia pieno d'acqua; la quale nello stesso modo
è costretta a seguitare il bicchiere, che la contiene, e alzarsi sopra l'altr'acqua nella
region dell'aria, che vien forzata l'aria a seguire il medesimo vaso sotto a' confini
dell'acqua, sin che in questo caso l'acqua, sopraffacendo gli orli del bicchiere, vi
precipita dentro, scacciandone l'aria, e in quello, uscendo il medesimo orlo fuori
dell'acqua e pervenendo a' confini dell'aria, l'acqua casca a basso e l'aria sottentra a
riempiere la cavità del vaso. Al che ne séguita, che non meno trapassi i limiti delle
convenzioni quello che produce una tavola congiunta con molta aria, per vedere se discende
al fondo nell'acqua, che quello che fa prova della resistenza all'esser sollevato in aria
con una falda di piombo congiunta con altrettanta acqua.
Ho detto quanto m'è venuto in mente, per mostrar la verità della parte che ho preso a
sostenere: restami da considerar ciò che in tale materia scrive Aristotile, nel fine de'
libri Del cielo. Nel qual particolare io noterò due cose: l'una, che essendo vero,
come s'è dimostrato, che la figura non ha che fare circa 'l semplicemente muoversi o non
muoversi in su o in giù, pare che Aristotile nel primo ingresso di questa speculazione
abbia avuto la medesima oppinione, sì come dall'essaminar le sue parole parmi che si
possa raccorre: bene è vero che, nel voler poi render la ragione di tal effetto, come
quegli che non l'ha, per quant'io stimo, bene incontrata, il che nel secondo luogo andrò
esaminando, par che si riduca ad ammetter l'ampiezza della figura a parte di
quest'operazione.
Quanto al primo punto, ecco le parole precise d'Aristotile: "Le figure non son
cause del muoversi semplicemente in giù o in su, ma del muoversi più tardo o più
veloce; e per quali cagioni ciò accaggia, non è difficile il vederlo".
Qui, primieramente, io noto che, essendo quattro i termini che cascono nella presente
considerazione, cioè moto, quiete, tardo e veloce, e nominando Aristotile le figure come
cause del tardo e del veloce, escludendole dall'esser cause del moto assoluto e semplice,
par necessario che egli l'escluda altresì dall'esser cause di quiete; sì che la mente
sua sia stata il dire: Le figure non son cause del muoversi assolutamente o non muoversi,
ma del tardo e del veloce. Imperocché, se alcuno dicesse, la mente d'Aristotile esser
d'escluder ben le figure dall'esser cause di moto, ma non già dall'esser cause di quiete,
sì che il senso fosse di rimuovere dalle figure l'esser cause del muoversi semplicemente,
ma non già l'esser cause del quietarsi; io domanderei, se si dee con Aristotile intendere
che tutte le figure universalmente sieno in qualche modo cause della quiete in quei corpi
che per altro si moverebbono, o pure alcune particolari solamente, come, per esempio, le
figure larghe e sottili. Se tutte indifferentemente, adunque ogni corpo quieterà, perché
ogni corpo ha qualche figura; il che è falso: ma se alcune particolari solamente potranno
essere in qualche modo causa di quiete, come, v. g., le larghe, adunque le altre saranno
in qualche modo causa di muoversi; perché, se dal vedere alcuni corpi di figura raccolta
muoversi, che poi, dilatati in falde, si fermano, posso inferir l'ampiezza della figura
essere a parte nella causa di tal quiete, così dal veder simil falde quietare, che poi
raccolte si muovono, potrò con pari ragione affermare, la figura unita e raccolta aver
parte nel cagionare 'l moto, come rimovente di chi l'impediva; il che è poi dirittamente
opposto a quello che dice Aristotile, cioè che le figure non son cause del muoversi. In
oltre, se Aristotile avesse ammesse, e non escluse, le figure all'esser cause del non
muoversi in alcuni corpi, che figurati d'altra figura si moverebbono, male a proposito
avrebbe, nelle parole immediatamente seguenti, proposto con modo dubitativo, "onde
avvenga che le falde larghe e sottili di ferro o di piombo si fermino sopra l'acqua",
già che la causa era in pronto, cioè l'ampiezza della figura. Concludasi, dunque, che 'l
concetto d'Aristotile in questo luogo sia d'affermare che le figure non sien cause del
muoversi assolutamente o non muoversi, ma solamente del muoversi velocemente o tardamente:
il che si dee tanto più credere, quanto che, in effetto, è sentenza e concetto
verissimo. Ora, essendo tale la mente d'Aristotile, e' apparendo, in conseguenza, più
presto contraria, nel primo aspetto, che favorevole al detto degli avversari, è forza che
la 'nterpretazion loro non sia precisamente tale, ma quale in parte intesi da alcun di
essi, e 'n parte da altri fu referto; e agevolmente si può stimare esser così, essendo
esplicazione conforme al senso d'interpreti celebri: ed è, che l'avverbio semplicemente
o assolutamente, posto nel testo, non si debba congiungere col verbo muoversi,
ma co 'l nome cause; sì che il sentimento delle parole d'Aristotile sia
l'affermare che le figure non son cause assolutamente del muoversi o non muoversi, ma son
ben cause secundum quid, cioè in qualche modo, per lo che vengon nominate cause
aiutrici e concomitanti. E tal proposizione vien ricevuta e posta per vera dal Sig.
Buonamico nel lib. 5, cap. 28, dove egli scrive così: "Sono altre cause
concomitanti, per le quali alcune cose galleggiano e altre si sommergono, tra le quali il
primo luogo ottengon le figure de' corpi, ec.".
Intorno a tal esposizione mi nascon diversi dubbi e difficultà, per le quali mi par
che le parole d'Aristotile non sien capaci di simil costruzione e sentimento. E le
difficultà son queste.
Prima, nell'ordine e disposizion delle parole d'Aristotile la particula simpliciter
o, vogliamo dire, absolute è attaccata col verbo si muovono, e separata
dalla parole cause: il che è gran presunzione a favor mio; poiché la scrittura e
'l testo dice: "Le figure non son cause del muoversi semplicemente in su o in giù,
ma sì bene del più tardo o più veloce"; e non dice: "Le figure non sono
semplicemente cause del muoversi in su o in giù"; e quando le parole d'un testo
ricevono, trasposte, senso differente da quello ch'elle suonano portate con l'ordine in
che l'autor le dispose, non conviene il permutarle. E chi vorrà affermare che Aristotile,
volendo scrivere una proposizione, disponesse le parole in modo ch'elle importassero un
sentimento diversissimo, anzi contrario? contrario, dico, perché, intese com'elle sono
scritte, dicono che le figure non son cause del muoversi; ma trasposte, dicono le figure
esser causa del muoversi, ec.
Di più, se la 'ntenzione d'Aristotile fusse stata di dire che le figure non son
semplicemente cause del muoversi in su o in giù, ma solamente cause secundum quid,
non occorreva che soggiugnesse quelle parole "ma son cause del più veloce o più
tardo". Anzi, il soggiugner questo sarebbe stato non solo superfluo, ma falso:
conciossiaché tutto il corso della proposizione importerebbe questo: "Le figure non
son causa assoluta del muoversi in su o in giù, ma son ben causa assoluta del tardo o del
veloce": il che non è vero; perché le cause primarie del più o men veloce vengon
da Aristotile, del 4 della Fisica, al testo 71, attribuite alla maggiore o minor
gravità de' mobili, paragonati tra di loro, e alla maggiore o minor resistenza de' mezzi,
dependente dalla lor maggiore o minor crassizie; e queste vengon poste da Aristotile come
cause primarie, e queste due sole vengono in quel luogo nominate; e la figura vien poi
considerata, al t. 74, più presto come causa strumentaria della forza della gravità, la
quale divide o con la figura o con l'impeto; e veramente la figura per sé stessa, senza
la forza della gravità o leggerezza, non opererebbe niente.
Aggiungo che, se Aristotile avesse avuto concetto che la figura fusse stata in qualche
modo causa del muoversi o non muoversi, il cercare, ch'e' fa immediatamente, in forma di
dubitare, onde avvenga che una falda di piombo soprannuoti, sarebbe stato a sproposito:
perché, se all'ora all'ora egli aveva detto che la figura era in certo modo causa del
muoversi o non muoversi, non occorreva volgere in dubbio per qual cagion la falda di
piombo galleggi, attribuendone poi la causa alla figura, e formando un discorso in questa
maniera: "La figura è causa secundum quid del non andare al fondo: ma ora si
dubita, per qual cagione una sottil falda di piombo non vada al fondo; si risponde, ciò
provenire dalla figura"; discorso che sarebbe indecente ad un fanciullo, non che ad
Aristotile. E dove è la occasione di dubitare? e chi non vede che, quando Aristotile
avesse stimato che la figura fosse in qualche modo causa del soprannotare, avrebbe, senza
la forma di dubitare, scritto: "La figura è causa in certo modo del soprannotare; e
però la falda di piombo, rispetto alla sua figura sparsa e larga, soprannuota"? Ma
se noi prenderemo la proposizione d'Aristotile come dico io e come è scritta, e come in
effetto è vera, il progresso suo cammina benissimo, sì nell'introduzione del veloce e
del tardo, come nella dubitazione, la qual molto a proposito ci cade; e dirà così:
"Le figure non son cause del muoversi o non muoversi semplicemente in su o in giù,
ma sì bene del muoversi più veloce o più tardo: ma se così è, si dubita della causa
onde avvenga che una falda larga e sottile di ferro o di piombo soprannuoti, ec.". E
l'occasion del dubitare è in pronto, perché pare, al primo aspetto, che di questo
soprannotare ne sia causa la figura, poiché lo stesso piombo, o minor quantità, ma
d'altra figura, va al fondo: e noi già abbiamo affermato, che la figura non ha azione in
questo effetto.
Finalmente, se la 'ntenzion d'Aristotile in questo luogo fusse stata di dir che le
figure, benché non assolutamente, sieno al manco in qualche modo cagion del muoversi o
non muoversi, io metto in considerazione che egli nomina non meno il movimento all'in su,
che l'altro all'in giù: e perché, nell'esemplificarlo poi, non si produce
altr'esperienza che d'una falda di piombo e d'una tavoletta d'ebano, materie che per lor
natura vanno in fondo, ma in virtù (come essi dicono) della figura restano a galla,
converrebbe che chi che sia producesse alcun'altra esperienza di quelle materie che per
lor natura vengono a galla, ma ritenute dalla figura restano in fondo. Ma già che
quest'è impossibile a farsi, concludiamo che Aristotile in questo luogo non ha voluto
attribuire azione alcuna alla figura, nel semplicemente muoversi o non muoversi.
Che poi egli abbia esquisitamente filosofato nell'investigar le soluzioni de' dubbi
ch'ei propone, non torre'io già a sostenere; anzi varie difficultà, che mi si
rappresentano, mi danno occasione di dubitare ch'ei non ci abbia interamente spiegata la
vera cagion della presente conclusione. Le quali diffucultà io andrò movendo, pronto al
mutar credenza, qualunque volta mi sia mostrato, altra, da quel ch'io dico, esser la
verità; alla confession della quale son molto più accinto, che alla contraddizione.
Proposta che ha Aristotile la quistione "onde avvenga che le falde larghe di ferro
o di piombo soprannuotino", soggiugne (quasi fortificando l'occasion del dubitare):
"conciosia che altre cose minori e manco gravi, se saranno rotonde o lunghe, come
sarebbe un ago, vanno al fondo". Or qui dubito, anzi pur son certo, che un ago,
posato leggiermente su l'acqua, resti a galla, non meno che le sottili falde di ferro e di
piombo.
Io non posso credere, ancorché stato mi sia referto, che alcuno, per difendere
Aristotile, dicesse che egli intende d'un ago messo non per lo lungo, ma eretto e per
punta: tuttavia, per non lasciare anche tal refugio, benché debolissimo e quale anche
Aristotile medesimo, per mio credere, ricuserebbe, dico che si dee intender che l'ago sia
posato secondo la dimensione che vien nominata da Aristotile, che è la lunghezza.
Perché, se altra dimensione che la nominata prender si potesse e dovesse, io direi che
anche le falde di ferro e di piombo vanno al fondo, se altri le metterà per taglio e non
per piano: ma perché Aristotile dice "le figure larghe non vanno al fondo", si
dee intender "posate per lo largo": e però quando dice "le figure lunghe,
come un ago, benché leggieri, non restano a galla", si dee intender "posate per
lo lungo".
 |
 |
Di più, il dir che
Aristotile intese |
|
|