Galileo Galilei Intorno alle cose che stanno in su l'acqua o che in quella si muovono Ottava pagina

Di più, il dir che Aristotile intese dell'ago messo per punta, é un fargli dire una sciocchezza grande: perché in questo luogo dice che piccole particelle di piombo o ferro, se saranno rotonde o lunghe com'un ago, vanno in fondo, tal che, anco per suo credere, un granello di ferro non può restare a galla; e se egli così credette, qual semplicità sarebbe stata il soggiugnere, che né anco un ago, messo eretto, vi sta? e che altro è un ago tale, che molti sì fatti grani posti l'un sopra l'altro? Troppo indegno di tant'uomo era il dir, che un sol grano di ferro non può galleggiare, e che né anco galleggerebbe a porgliene cento altri addosso.

Finalmente, o Aristotile credeva che un ago, posato su l'acqua per lo lungo, restasse a galla; o credeva ch'e' non restasse. S'ei credeva ch'e' non restasse, ha ben potuto anche dirlo, come veramente l'ha detto: ma s'e' credeva e sapeva ch'e' soprannotasse, per qual cagione, insieme col problema dubitativo del galleggiar le figure larghe, benché di materia grave, non ha egli anche introdotta la dubitazione, ond'avvegna che anche le figure lunghe e sottili, benché di ferro o di piombo, soprannuotano? e massimamente che l'occasion del dubitare par maggiore nelle figure lunghe e strette che nelle larghe e sottili; sì come dal non n'aver dubitato Aristotile si fa manifesto.

Non minore sproposito addosserebbe ad Aristotile chi, per difenderlo, dicesse che egli intese di un ago assai grosso, e non di un sottile: perché io pur domanderò ciò ch'e' credette d'un ago sottile, e bisognerà risponder ch'e' credesse ch'e' galleggiasse; ed io di nuovo l'accuserò dell'avere sfuggito un problema più maraviglioso e difficile, ed introdotto il più facile e di meraviglia minore.

Diciamo, dunque, pur liberamente, che Aristotile ha creduto che le figure larghe solamente stessero a galla; ma le lunghe e sottili, com'un ago, no: il che tuttavia è falso, come falso è ancor de' corpi rotondi; perché, come dalle cose di sopra dimostrate si può raccorre, piccoli globetti di ferro, e anche di piombo, nello stesso modo galleggiano.

Propone poi un'altra conclusione, che similmente par diversa dal vero: ed è, che alcune cose per la lor piccolezza nuotano nell'aria, come la minutissima polvere di terra e le sottili foglie dell'oro battuto. Ma a me pare che la sperienza ci mostri, ciò non accadere non solamente nell'aria, ma né anche nell'acqua; nella quale discendono sino a quelle particole di terra che la 'ntorbidano, la cui piccolezza è tale che non si veggono, se non quando son molte centinaia insieme. La polvere, dunque, di terra, e l'oro battuto, non si sostiene altramente in aria, ma discende al basso, e solamente vi va vagando quando venti gagliardi la sollevano o altra agitazione di aria la commuove: il che anche avviene nella commozione dell'acqua, per la quale si solleva la sua deposizione dal fondo, e s'intorbida. Ma Aristotile non può intender di questo impedimento della commozione, del quale egli non fa menzione; né nomina altro che la leggerezza di tali minimi, e la resistenza della crassizie dell'acqua e dell'aria: dal che si vede che egli tratta dell'aria quieta, e non agitata e commossa; ma, in tal caso, né oro né terra, per minutissimi che sieno, si sostengono, anzi speditamente discendono.

Passa poi al confutar Democrito, il qual, per sua testimonianza, voleva che alcuni atomi ignei, li quali continuamente ascendono per l'acqua, spignessero in su e sostenessero quei corpi gravi che fossero molto larghi, e che gli stretti scendessero al basso, perché poca quantità de' detti atomi contrasta loro e repugna.

Confuta, dico, Aristotile questa posizione, dicendo che ciò doverrebbe molto più accader nell'aria; sì come il medesimo Democrito insta contro di sé, ma, dopo aver mossa l'instanza, la scioglie lievemente, con dire che quei corpuscoli, che ascendono in aria, fanno impeto non unitamente. Qui io non dirò che la cagione addotta da Democrito sia vera: ma dirò solo, parermi che non interamente venga confutata da Aristotile, mentr'egli dice che, se fusse vero che gli atomi calidi, che ascendono, sostenessero i corpi gravi, ma assai larghi, ciò dovrieno far molto più nell'aria che nell'acqua; perché forse, per opinion d'Aristotile, i medesimi corpuscoli calidi con maggior forza e velocità sormontano per l'aria che per l'acqua. E se questa è, sì come io credo, l'instanza d'Aristotile, parmi d'aver cagione di dubitar ch'e' possa essersi ingannato in più d'un conto.

Prima: perché que' calidi, o sieno corpuscoli ignei, o sieno esalazioni, o in somma sieno qualunque materia che anche in aria ascenda in su, non è credibile che più velocemente salgano per l'aria che per l'acqua; anzi, all'incontro, per avventura, più impetuosamente si muovono per l'acqua che per l'aria, come in parte di sopra ho dimostrato. E qui non so scorger la cagione, per la quale Aristotile, vedendo che 'l moto all'in giù, dello stesso mobile, è più veloce nell'aria che nell'acqua, non ci abbia fatti cauti che del moto contrario dee accader l'opposito di necessità, cioè ch'e' sia più veloce nell'acqua che nell'aria: perché, avvenga che 'l mobile, che discende, più velocemente si muove per l'aria che per l'acqua, se noi c'immagineremo che la sua gravità si vada gradatamente diminuendo, egli prima diverrà tale che, scendendo velocemente nell'aria, tardissimamente scenderà nell'acqua; di poi potrà esser tale che, scendendo pure ancora per l'aria, ascenda nell'acqua; e fatto ancora men grave, ascenderà velocemente per l'acqua, e pur discenderà ancora per l'aria; e in somma, avanti ch'ei cominci a potere ascender, benché tardissimamente, per l'aria, velocissimamente sormonterà per l'acqua. Come dunque è vero, che quel che si muove all'in su, più velocemente si muova per l'aria che per l'acqua? Quel ch'ha fatto credere ad Aristotile, il moto in su farsi più velocemente in aria che in acqua, è stato, prima, l'aver riferite le cause del tardo e del veloce, tanto del moto in su quanto dello in giù, solamente alla diversità delle figure del mobile e alla maggiore o minor resistenza della maggior o minor crassizie o sottilità del mezzo, non curando la comparazion degli eccessi delle gravità de' mobili e de' mezzi: la qual tuttavia è 'l punto principalissimo in questa materia. Che se l'incremento e 'l decremento della tardità o velocità non avessero altro rispetto che alla grossezza o sottilità de' mezzi, ogni mobile, che scendesse per l'aria, scenderebbe anche per l'acqua: perché qualunque differenza si ritrovi tra la crassizie dell'acqua e quella dell'aria, può benissimo ritrovarsi tra la velocità dello stesso mobile nell'aria e qualche altra velocità; e questa dovrebbe esser sua propria nell'acqua: il che tuttavia è falsissimo. L'altra occasione è, che egli ha creduto che, sì come c'è una qualità positiva e intrinseca per la quale i corpi elementari hanno propensione di muoversi verso il centro della terra, così ce ne sia un'altra, pure intrinseca, per la quale alcuni di tali corpi abbiano impeto di fuggire 'l centro e muoversi all'in su, in virtù del qual principio intrinseco, detto da lui leggierezza, i mobili di tal moto più agevolmente fendano i mezzi più sottili che i più crassi: ma tal posizione mostra parimente di non esser sicura, come di sopra accennai in parte, e come con ragioni ed esperienze potrei mostrare, se l'occasion presente n'avesse maggior necessità, o se con poche parole potessi spedirmi.

L'instanza, dunque, di Aristotile contro a Democrito, mentre dice che, se gli atomi ignei ascendenti sostenessero i corpi gravi ma di figura larga, ciò dovrebbe avvenire maggiormente nell'aria che nell'acqua, perché tali corpuscoli più velocemente si muovono in quella che in questa, non è buona; anzi dee appunto accader l'opposito, perché più lentamente ascendono per l'aria: e, oltre al muoversi lentamente, non vanno uniti insieme, come nell'acqua, ma si discontinuano e, come diciamo noi, si sparpagliano; e però, come ben risponde Democrito risolvendo l'instanza, non vanno a urtare e fare impeto unitamente.

S'inganna, secondariamente, Aristotile, mentre e' vuole che detti corpi gravi più agevolmente fossero da calidi ascendenti sostenuti nell'aria che nell'acqua: non avvertendo che i medesimi corpi sono molto più gravi in quella che in questa, e che tal corpo peserà dieci libre in aria, che nell'acqua non peserà mezz'oncia; come, dunque, dovrà esser più agevole il sostenerlo nell'aria che nell'acqua?

Concludasi, per tanto, che Democrito in questo particolare ha meglio filosofato che Aristotile. Ma non però voglio io affermare che Democrito abbia rettamente filosofato, anzi pure dirò io che c'è esperienza manifesta che distrugge la sua ragione: e questa è che, s'e' fosse vero che atomi caldi ascendenti nell'acqua sostenessero un corpo che, senza 'l loro ostacolo, anderebbe al fondo, ne seguirebbe che noi potessimo trovare una materia pochissimo superiore in gravità all'acqua, la quale, ridotta in una palla o altra figura raccolta, andasse al fondo, come quella che incontrasse pochi atomi ignei, e che, distesa poi in una ampia e sottil falda, venisse sospinta in alto dalle impulsioni di gran moltitudine de' medesimi corpuscoli, e poi trattenuta al pelo della superficie dell'acqua; il che non si vede accadere, mostrandoci l'esperienza che un corpo di figura, v. g., sferica, il quale a pena e con grandissima tardità va al fondo, vi resterà e vi discenderà ancora, ridotto in qualunque altra larghissima figura. Bisogna dunque dire, o che nell'acqua non sieno tali atomi ignei ascendenti, o, se vi sono, che non sieno potenti a sollevare e spignere in su alcuna falda di materia che, senza loro, andasse al fondo. Delle quali due posizioni io stimo che la seconda sia vera, intendendo dell'acqua constituita nella sua natural freddezza: ma se noi piglieremo un vaso, di vetro o di rame o di qual si voglia altra materia dura, pieno d'acqua fredda, dentro la quale si ponga un solido di figura piana o concava, ma che in gravità ecceda l'acqua così poco che lentamente si conduca al fondo, dico che, mettendo alquanti carboni accesi sotto il detto vaso, come prima i nuovi corpuscoli ignei, penetrata la sustanzia del vaso, ascenderanno per quella dell'acqua, senza dubbio, urtando nel solido sopraddetto, lo spigneranno sino alla superficie, e quivi lo tratterranno sin che dureranno le incursioni de' detti corpuscoli; le quali cessando dopo la suttrazion del fuoco, tornerà il solido al fondo, abbandonato da' suoi puntelli. Ma nota Democrito, che questa causa non ha luogo se non quando si tratti d'alzare e sostenere falde di materie poco più gravi dell'acqua o vero sommamente sottili; ma in materie gravissime e di qualche grossezza, come falde di piombo o d'altri metalli, cessa totalmente un tale effetto. In testimonio di che, notisi che tali falde, sollevate da gli atomi ignei, ascendono per tutta la profondità dell'acqua e si fermano al confin dell'aria, restando però sott'acqua; ma le falde degli avversari non si fermano se non quando hanno la superficie superiore asciutta, né vi è mezzo d'operare che, quando sono dentr'all'acqua, non calino al fondo. Altra, dunque, è la causa del soprannotare le cose delle quali parla Democrito, e altra quella delle cose delle quali parliamo noi.

Ma, tornando ad Aristotile, parmi che egli assai più freddamente confuti Democrito, che lo stesso Democrito non fa, per detto d'Aristotile, l'istanze che egli si muove contro: e l'oppugnarlo con dire che, se i calidi ascendenti fossero quelli che sollevassero le sottil falde, molto più dovrebbe un tal solido esser sospinto e sollevato per aria, mostra in Aristotile la voglia d'atterrar Democrito superiore all'esquisitezza del saldo filosofare. Il qual desiderio in altre occasioni si scuopre, e, senza molto discostarsi da questo luogo, nel testo precedente a questo capitolo che abbiamo per le mani: dov'ei tenta pur di confutare il medesimo Democrito, perché egli, non si contentando del nome solo, aveva voluto più particolarmente dichiarare che cosa fusse la gravità e la leggerezza, cioè la causa dell'andare in giù e dell'ascendere, e aveva introdotto il pieno e 'l vacuo, dando questo al fuoco, per lo quale si movesse in su, e quello alla terra, per lo quale ella discendesse, attribuendo poi all'aria più del fuoco e all'acqua più della terra. Ma Aristotile, volendo anche del moto all'in su una causa positiva e non, come Platone o questi altri, una semplice negazione o privazione, qual sarebbe il vacuo referito al pieno, argomenta contro a Democrito, e dice: Se è vero quanto tu supponi, adunque sarà una gran mole d'acqua la quale avrà più di fuoco che una piccola mole d'aria, e una grande d'aria che avrà più terra che una piccola d'acqua; il perché bisognerebbe che una gran mole d'aria venisse più velocemente a basso che una piccola quantità d'acqua: ma ciò non si vede mai in alcun modo: adunque Democrito erroneamente discorre. Ma, per mia opinione, la dottrina di Democrito non resta per tale instanza abbattuta; anzi, s'io non erro, la maniera di dedurre d'Aristotile o non conclude, o, se è concludente, altrettanto si potrà ritorcer contro di lui. Concederà Democrito ad Aristotile, che si possa pigliare una gran mole d'aria, la quale contenga più di terra che una piccola quantità d'acqua; ma ben negherà che tal mole d'aria sia per andar più velocemente a basso che una poca acqua: e questo per più ragioni. Prima, perché, se la maggior quantità di terra, contenuta nella gran mole d'aria, dovesse esser cagione di velocità maggiore che minor quantità di terra contenuta nella piccola mole d'acqua, bisognerebbe prima che fusse vero che una maggior mole di terra semplice si movesse più velocemente che una minore: ma quest'è falso, benché Aristotile in più luoghi l'affermi per vero; perché non la maggior gravità assoluta, ma la maggior gravità in ispecie, è cagione di velocità maggiore; né più velocemente discende una palla di legno che pesi dieci libbre, che una che pesi dieci once e sia della stessa materia; ma ben discende più velocemente una palla di piombo di quattro once, che una di legno di venti libbre, perché 'l piombo è in ispecie più grave del legno: adunque non è necessario che una gran mole d'aria, per la molta terra contenuta in essa, discenda più velocemente che piccola mole d'acqua; anzi, per l'opposito, qualunque mole d'acqua dovrà muoversi più veloce di qualunque altra d'aria, per esser la participazion della parte terrea in ispecie maggior nell'acqua che nell'aria. Notisi, nel secondo luogo, come, nel multiplicar la mole dell'aria, non si multiplica solamente quello che vi è di terreo, ma il suo fuoco ancora: onde non meno se le cresce la causa dell'andare in su, in virtù del fuoco, che quella del venire all'ingiù, per conto della sua terra multiplicata. Bisognava, nel crescer la grandezza dell'aria, multiplicar quello che ella ha di terreo solamente, lasciando il suo primo fuoco nel suo stato: ché allora, superando 'l terreo dell'aria augumentata la parte terrea della piccola quantità dell'acqua, si sarebbe potuto più verisimilmente pretender che con impeto maggiore dovesse scender la molta quantità dell'aria che la poca acqua. È, dunque, la fallacia più nel discorso d'Aristotile che in quello di Democrito; il quale, con altrettanta ragione, potrebbe impugnare Aristotile, e dire: Se è vero che gli estremi elementi sieno l'uno semplicemente grave e l'altro semplicemente lieve, e che i medii partecipino dell'una e dell'altra natura, ma l'aria più della leggerezza, e l'acqua più della gravità; adunque sarà una gran mole d'aria la cui gravità supererà la gravità d'una piccola quantità d'acqua, e però tal mole d'aria discenderà più velocemente che quella poca acqua: ma ciò non si vede mai accadere: adunque non è vero che gli elementi di mezzo sieno partecipi dell'una e dell'altra qualità. Simile argomento è fallace, non meno che l'altro contr'a Democrito.

Ultimamente, avendo Aristotile detto che, se la posizion di Democrito fusse vera, bisognerebbe che una gran mole d'aria si movesse più velocemente che una piccola d'acqua, e poi soggiunto che ciò non si vede mai in alcun modo; parmi che altri possa restar con desiderio d'intender da lui, in qual luogo dovrebbe accader questo ch'e' deduce contro a Democrito, e quale esperienza ne insegni ch'e' non v'accaggia. Il creder di vederlo nell'elemento dell'acqua o 'n quel dell'aria, è vano, perché né l'acqua per acqua né l'aria per aria si muovono o moverebbon giammai, per qualunque participazione altri assegni loro di terra o di fuoco: la terra, per non esser corpo fluido e cedente alla mobilità d'altri corpi, è luogo e mezzo inettissimo a simile esperienza: il vacuo, per detto d'Aristotile medesimo, non si dà, e, benché si desse, nulla si moverebbe in lui: resta la region del fuoco; ma essendo per tanto spazio distante da noi, quale esperienza potrà assicurarci, o avere accertato Aristotile, in maniera ch'e' si debba, come di cosa notissima al senso, affermare quanto e' produce in confutazion di Democrito, cioè che non più velocemente si muova una gran mole d'aria che una piccola d'acqua? Ma io non voglio più lungamente dimorare in questa materia, dove sarebbe che dire assai: e, lasciato anche Democrito da una banda, torno al testo d'Aristotile, nel quale egli si va accingendo per render le vere cause onde avvenga che le sottil falde di ferro o di piombo soprannuotino all'acqua, e più l'oro stesso, assottigliato in tenuissime foglie, e la minuta polvere, non pure nell'acqua, ma nell'aria ancora, vadano notando; e pone che, de' continui, altri sieno agevolmente divisibili e altri no, e che, degli agevolmente divisibili, alcuni sien più e altri meno tali; e queste afferma dovere stimarsi che sien le cagioni. Soggiugne poi, quello essere agevolmente divisibile che ben si termina, e più quello che più, e tale esser più l'aria che l'acqua, e l'acqua che la terra. E ultimamente suppone, che in ciascun genere più agevolmente si divide e si distrae la minor quantitade che la maggiore.

Qui io noto, che le conclusion d'Aristotile in genere son tutte vere, ma parmi che egli le applichi a particolari ne' quali esse non hanno luogo, come bene lo hanno in altri: come, v. gr., la cera è più agevolmente divisibile che il piombo, e il piombo che l'argento; sì come la cera più agevolmente riceve tutti i termini che 'l piombo, e 'l piombo che l'argento. È vero, in oltre, che più agevolmente si divide poca quantità d'argento che una gran massa: e tutte queste proposizioni son vere, perché vero è che nell'argento nel piombo e nella cera è semplicemente resistenza all'esser diviso, e dov'è l'assoluto è anche il respettivo. Ma se tanto nell'acqua, quanto nell'aria, non è renitenza alcuna alla semplice divisione, come potremo dire che più difficilmente dividasi l'acqua che l'aria? Noi non ci sappiamo staccare dall'equivocazione: onde io torno a replicare, che altra cosa è il resistere alla divisione assoluta, altra il resistere alla division fatta con tanta e tanta velocità. Ma per far la quiete e ostare al moto, è necessaria la resistenza alla divisione assoluta; e la resistenza alla presta divisione cagiona non la quiete, ma la tardità del moto: ma che tanto nell'aria, quanto nell'acqua, la resistenza alla semplice division non vi sia, è manifesto; perché niun corpo solido si trova, il quale non divida l'aria e l'acqua ancora. E che l'oro battuto o la minuta polvere non sieno potenti a superar la renitenza dell'aria, è contrario a quello che l'esperienza ci mostra, vedendosi e l'oro e la polvere andar vagando per l'aria e finalmente discendere al basso, e fare anche lo stesso nell'acqua, se vi saranno locati dentro e separati dall'aria. E perché, come io dico, né l'acqua né l'aria resistono punto alla semplice divisione, non si può dir che l'acqua resista più che l'aria. Né sia chi m'opponga l'esemplo di corpi leggerissimi, come d'una penna o d'un poco di midolla di sagginale o di canna palustre che fende l'aria e l'acqua no, e che da questo voglia poi inferire, l'aria esser più agevolmente divisibile che l'acqua: perché io gli dirò che, s'egli ben osserverà, vedrà il medesimo solido dividere ancora la continuità dell'acqua, e sommergersi una parte di lui, e parte tale che altrettanta acqua in mole peserebbe quanto tutto lui. E se pure egli persistesse nel dubitare che tal solido non si profondasse per impotenza di divider l'acqua, io tornerò a dirgli ch'e' lo spinga sotto acqua, e vedrallo poi, messo ch'e' l'abbia in sua libertà, divider l'acqua ascendendo, non men prontamente ch'e' si dividesse l'aria discendendo. Sì che il dire "Questo tal solido scende nell'aria, ma giunto all'acqua cessa di muoversi; e però l'acqua più difficilmente si divide", non conclude niente; perché io, all'incontro, gli proporrò un legno o un pezzo di cera, il quale dal fondo dell'acqua si eleva e agevolmente si divide la sua resistenza, che poi, arrivato all'aria, si ferma e a pena la intacca; onde io potrò, con altrettanta ragione, dire che l'acqua più agevolmente si divide che l'aria.

Io non voglio, in questo proposito, restar d'avvertire un'altra fallacia di questi pure che attribuiscono la cagion dell'andare o non andare al fondo, alla minore o maggior resistenza della crassizie dell'acqua all'esser divisa, servendosi dell'esemplo d'un uovo, il quale nell'acqua dolce va al fondo, ma nella salsa galleggia, e adducendo per cagion di ciò la poca resistenza dell'acqua dolce all'esser divisa, e la molta dell'acqua salsa. Ma, s'io non erro, dalla stessa esperienza si può non meno dedurre anche tutto l'opposito, cioè che l'acqua dolce sia più crassa, e la salsa più tenue e sottile; poiché un uovo dal fondo dell'acqua salsa speditamente ascende al sommo e divide la sua resistenza, il che non può egli fare nella dolce, nel cui fondo resta senza poter sollevarsi ad alto. A simili angustie conducono i falsi principii: ma chi, rettamente filosofando, riconoscerà per cagioni di tali effetti gli eccessi della gravità de' mobili e de' mezzi, dirà che l'uovo va al fondo nell'acqua dolce perché è più grave di lei, e viene a galla nella salsa perché è men grave di quella; e senza intoppo alcuno molto saldamente stabilirà le sue conclusioni.

Cessa, dunque, totalmente la ragione che Aristotile soggiugne nel testo, dicendo: "Le cose, dunque, che hanno gran larghezza, restano sopra, perché comprendono assai; e quello che è maggiore, non agevolmente si divide"; cessa, dico, tal discorso, perché non è vero che nell'acqua o nell'aria sia resistenza alcuna alla divisione; oltreché la falda di piombo, quando si ferma, ha già divisa e penetrata la crassizie dell'acqua, e profondatasi dieci e dodici volte più che non è la sua propria grossezza. Oltre che, tal resistenza all'esser divisa quando pur fusse nell'acqua, sarebbe semplicità il dir che ella fusse più nelle parti superiori che nelle medie e più basse: anzi, se differenza vi dovesse essere, dovrieno le più crasse esser le inferiori, sì che la falda non meno dovrebbe essere inabile a penetrare le parti più basse, che le superiori dell'acqua; tuttavia noi veggiamo che non prima si bagna la superficie superior della lamina, che ella precipitosamente e senza alcun ritegno discende sino al fondo.

Io non credo già che alcuno (stimando forse di potere in tal guisa difendere Aristotile) dicesse che, essendo vero che la molta acqua resiste più che la poca, la detta lamina, fatta più bassa, discenda perché minor mole d'acqua gli resti da dividere: perché, se dopo l'aver veduta la medesima falda galleggiare in un palmo d'acqua e anche poi nella medesima sommergersi, e' tenterà la stessa esperienza sopra una profondità di dieci o venti braccia, vedrà seguirne il medesimo effetto per appunto. E qui torno a ricordare, per rimuovere un errore assai comune, che quella nave, o altro qual si voglia corpo, che sopra la profondità di cento o di mille braccia galleggia col tuffar solamente sei braccia della sua propria altezza, galleggerà nello stesso modo appunto nell'acqua che non abbia maggior profondità di sei braccia e un mezzo dito. Né credo altresì che si possa dir, le parti superiori dell'acqua esser le più crasse, benché gravissimo autore abbia stimato, nel mare l'acque superiori esser tali, pigliandone argomento dal ritrovarsi più salate che quelle del fondo: ma io dubiterei dell'esperienza, se già nell'estrar l'acqua del fondo non s'incontrasse qualche polla d'acqua dolce, che quivi scaturisse: ma ben veggiamo, all'incontro, l'acque dolci de' fiumi dilatarsi, anche per alcune miglia, oltre alle lor foci sopra l'acqua salsa del mare, senza discendere in quella o con essa confondersi, se già non accade qualche commozione e turbamento de' venti.

Ma, tornando ad Aristotile, gli dico che la larghezza della figura non ha che fare in questo negozio né punto né poco; perché la stessa falda di piombo, o d'altra materia, fattone strisce quanto si voglia strette, soprannuota né più né meno; e lo stesso faranno le medesime strisce di nuovo tagliate in piccoli quadretti, perché non la larghezza, ma la grossezza, è quella che opera in questo fatto. Dicogli, di più, che, quando ben fusse vero che la renitenza alla divisione fusse la propria cagione del galleggiare, molto e molto meglio galleggerebbono le figure più strette e più corte che le più spaziose e larghe; sì che, crescendo l'ampiezza della figura, si diminuirebbe l'agevolezza del soprannotare, e scemando quella, si crescerebbe questa.

E, per dichiarazione di quanto io dico, metto in considerazione che, quando una sottil falda di piombo discende dividendo l'acqua, la divisione e discontinuazione si fa tra le parti dell'acqua che sono intorno intorno al perimetro e circonferenza di essa falda; e secondo la grandezza maggiore o minore di tal circuito, ha da dividere maggiore o minor quantità d'acqua: sì che, se il circuito, v. g., d'una tavola sarà dieci braccia, nel profondarla per piano si ha da far la separazione e divisione e, per così dire, un taglio su dieci braccia di lunghezza d'acqua; e similmente una falda minore, che abbia quattro braccia di perimetro, dee fare un taglio di quattro braccia. 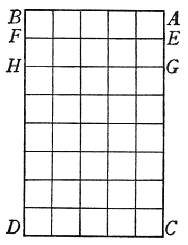Stante questo, chi avrà un po' di geometria comprenderà non solamente che una tavola, segata in molte strisce, assai meglio soprannoterà che quando era intera, ma che tutte le figure, quanto più saranno corte e strette, tanto meglio doveranno stare a galla.  Sia la tavola ABCD, lunga, per esemplo, otto palmi e larga cinque: sarà il suo ambito palmi venzei; e venzei palmi sarà la lunghezza del taglio, ch'ella dee far nell'acqua per discendervi. Ma se noi la segheremo, v. g., in otto tavolette, secondo le linee EF, GH, ec., facendo sette segamenti, verremo ad aggiugnere alli venzei palmi del circuito della tavola intera altri settanta di più; onde le otto tavolette, così segate e separate, avranno a tagliare novanzei palmi d'acqua: e se, di più, segheremo ciascuna delle dette tavolette in cinque parti, riducendole in quadrati, alli circuiti di palmi novanzei, con quattro tagli d'otto palmi l'uno, n'aggiugneremo ancora palmi sessantaquattro; onde i detti quadrati, per discender nell'acqua, dovranno dividere censessanta palmi d'acqua. Ma la resistenza di censessanta è assai maggiore che quella di venzei: adunque, a quanto minori superficie noi ci condurremo, tanto vedremo che più agevolmente galleggerebbono. E lo stesso interverrà di tutte l'altre figure, le cui superficie sieno fra di loro simili, ma differenti in grandezza; perché, diminuite o cresciute quanto si voglia le dette superficie, sempre con subdupla proporzione scemano o crescono i loro perimetri, cioè le resistenze ch'e' trovano in fender l'acqua: adunque più agevolmente galleggeranno di mano in mano le falde e tavolette, secondo ch'elle saranno di minore ampiezza.

Ciò è manifesto: perché, mantenendosi sempre la medesima altezza del solido, con la medesima proporzione che si cresce o scema la base, cresce ancora o scema l'istesso solido, onde, scemando più 'l solido che 'l circuito, più scema la causa dell'andare in fondo che la causa del galleggiare; ed all'incontro, crescendo più 'l solido che 'l circuito, più cresce la causa dell'andar in fondo, e meno quella del restar a galla.

E questo tutto seguirebbe in dottrina d'Aristotile, contr'alla sua medesima dottrina.

Finalmente, a quel che si legge nell'ultima parte del testo, cioè che si dee comparar la gravità del mobile con la resistenza del mezzo alla divisione, perché se la virtù della gravità eccederà la resistenza del mezzo, il mobile discenderà, se no, soprannoterà; non occorre risponder altro che quel che già s'è detto, cioè che non la resistenza alla divisione assoluta, la quale non è nell'acqua o nell'aria, ma la gravità del mezzo, si dee chiamare in paragone con la gravità del mobile: la qual se sarà maggior nel mezzo, il mobile non vi discenderà, né meno vi si tufferà tutto, ma una parte solamente; perché nel luogo ch'egli occuperebbe nell'acqua, non vi dee dimorar corpo che pesi manco d'altrettant'acqua: ma se 'l mobile sarà egli più grave, discenderà al fondo, ad occupare un luogo dov'è più conforme alla natura che vi dimori egli, che altro corpo men grave. E questa è la sola, vera, propria e assoluta cagione del soprannotare o andare al fondo, sì che altra non ve n'ha parte: e la tavoletta degli avversari soprannuota, quando è accoppiata con tanta d'aria, che insieme con essa forma un corpo men grave di tanta acqua quanta andrebbe a riempiere il luogo da tal composto occupato nell'acqua; ma quando si metterà nell'acqua il semplice ebano, conforme al tenor della nostra quistione, andrà sempre al fondo, benché fosse sottile come una carta.

IL FINE

Io Francesco Nori, Canonico Fiorentino, avendo rivista la presente opera, non ho in essa notato cosa alcuna disforme dalla pietà Cristiana né da' buon costumi, e la giudico degna delle stampe.

Niccolò dell'Antella Senatore.