 |
Galileo Galilei
Intorno alle cose che stanno in su l'acqua o che in quella si muovonoTerza pagina |
Il che dichiarato e supposto, vengo a dimostrare la verità di quanto ho accennato,
formando il seguente teorema.
La mole dell'acqua che si alza nell'immergere un prisma o cilindro solido, o che
s'abbassa nell'estrarlo, è minore della mole di esso solido demersa o estratta; e ad essa
ha la medesima proporzione, che la superficie dell'acqua circunfusa al solido alla
medesima superficie circunfusa insieme con la base del solido.
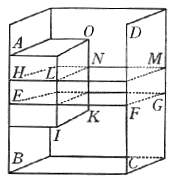 Sia il vaso ABCD, ed in esso l'acqua alta sino al livello EFG, avanti che il
prisma solido HIK vi sia immerso; ma dopo che egli è demerso, siasi sollevata l'acqua
sino al livello LM: sarà dunque già il solido HIK tutto sott'acqua, e la mole dell'acqua
alzata sarà LG, la quale è minore della mole del solido demerso, cioè di HIK, essendo
eguale alla sola parte EIK, che si trova sotto il primo livello EFG. Il che è manifesto:
perché se si cavasse fuori il solido HIK, l'acqua LG tornerebbe nel luogo occupato dalla
mole EIK, dove era contenuta avanti l'immersione del prisma: ed essendo la mole LG eguale
alla mole EK, aggiunta comunemente la mole EN, sarà tutta la mole EM, composta della
parte del prisma EN e dell'acqua NF, eguale a tutto 'l solido HIK, e però la mole LG alla
EM arà la medesima proporzione che alla mole HIK: ma la mole LG alla mole EM ha la
medesima proporzione che la superficie LM alla superficie MH: adunque é manifesto, la
mole dell'acqua sollevata LG alla mole del solido demerso HIK aver la medesima proporzione
che la superficie LM, che è quella dell'acqua ambiente il solido, a tutta la superficie
HM, composta della detta ambiente e della base del prisma HN. Ma se intenderemo, il primo
livello dell'acqua essere secondo la superficie HM, ed il prisma già demerso HIK esser
poi estratto ed alzato sino in EAO, e l'acqua essersi abbassata dal primo livello HLM sino
in EFG, è manifesto che, essendo il prisma EAO l'istesso che HIK, la parte sua superiore
HO sarà eguale all'inferiore EIK, rimossa la parte comune EN; ed, in conseguenza, la mole
dell'acqua LG essere eguale alla mole HO, e però minore del solido che si trova fuor
dell'acqua, che è tutto 'l prisma EAO, al quale similmente essa mole d'acqua abbassata LG
ha la medesima proporzione che la superficie dell'acqua circumfusa LM alla medesima
superficie circumfusa insieme con la base del prisma AO: il che ha la medesima
dimostrazione che l'altro caso di sopra. Sia il vaso ABCD, ed in esso l'acqua alta sino al livello EFG, avanti che il
prisma solido HIK vi sia immerso; ma dopo che egli è demerso, siasi sollevata l'acqua
sino al livello LM: sarà dunque già il solido HIK tutto sott'acqua, e la mole dell'acqua
alzata sarà LG, la quale è minore della mole del solido demerso, cioè di HIK, essendo
eguale alla sola parte EIK, che si trova sotto il primo livello EFG. Il che è manifesto:
perché se si cavasse fuori il solido HIK, l'acqua LG tornerebbe nel luogo occupato dalla
mole EIK, dove era contenuta avanti l'immersione del prisma: ed essendo la mole LG eguale
alla mole EK, aggiunta comunemente la mole EN, sarà tutta la mole EM, composta della
parte del prisma EN e dell'acqua NF, eguale a tutto 'l solido HIK, e però la mole LG alla
EM arà la medesima proporzione che alla mole HIK: ma la mole LG alla mole EM ha la
medesima proporzione che la superficie LM alla superficie MH: adunque é manifesto, la
mole dell'acqua sollevata LG alla mole del solido demerso HIK aver la medesima proporzione
che la superficie LM, che è quella dell'acqua ambiente il solido, a tutta la superficie
HM, composta della detta ambiente e della base del prisma HN. Ma se intenderemo, il primo
livello dell'acqua essere secondo la superficie HM, ed il prisma già demerso HIK esser
poi estratto ed alzato sino in EAO, e l'acqua essersi abbassata dal primo livello HLM sino
in EFG, è manifesto che, essendo il prisma EAO l'istesso che HIK, la parte sua superiore
HO sarà eguale all'inferiore EIK, rimossa la parte comune EN; ed, in conseguenza, la mole
dell'acqua LG essere eguale alla mole HO, e però minore del solido che si trova fuor
dell'acqua, che è tutto 'l prisma EAO, al quale similmente essa mole d'acqua abbassata LG
ha la medesima proporzione che la superficie dell'acqua circumfusa LM alla medesima
superficie circumfusa insieme con la base del prisma AO: il che ha la medesima
dimostrazione che l'altro caso di sopra.
E di qui si raccoglie, che la mole dell'acqua che s'alza nell'immersion del solido, o
che s'abbassa nell'estrarlo, non è eguale a tutta la mole del solido che si trova demersa
o estratta, ma a quella parte solamente, che nell'immersione resta sotto il primo livello
dell'acqua, e nell'estrazione riman sopra simil primo livello: che è quello che doveva
esser dimostrato. Seguiteremo ora le altre cose.
E prima dimostrerremo, che quando in uno de' vasi sopraddetti, di qualunque
larghezza, benché immensa o angusta, sia collocato un tal prisma o cilindro, circondato
da acqua, se alzeremo tal solido a perpendicolo, l'acqua circunfusa s'abbasserà; e
l'abbassamento dell'acqua all'alzamento del prisma avrà la medesima proporzione, che
l'una delle base del prisma alla superficie dell'acqua circunfusa.
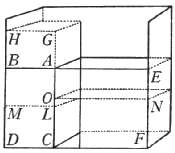 Sia
nel vaso, qual si è detto, collocato il prisma ACDB, e nel resto dello spazio
infusa l'acqua, sino al livello EA; e alzandosi il solido AD, sia trasferito
in GM, e l'acqua s'abbassi da EA in NO: dico che la scesa dell'acqua,
misurata dalla linea AO, alla salita del prisma, misurata dalla linea GA, ha
la stessa proporzione, che la base del solido GH alla superficie dell'acqua NO.
Il che è manifesto: perché la mole del solido GABH, alzata sopra 'l primo livello
EAB, è eguale alla mole dell'acqua, che si è abbassata, ENOA: son dunque
due prismi eguali, ENOA e GABH: ma de' prismi eguali le base rispondono
contrariamente alle altezze: adunque, come l'altezza OA all'altezza AG,
così è la superficie o base GH alla superficie dell'acqua NO. Quando
dunque, per esemplo, una colonna fusse collocata in piede in un grandissimo vivaio pieno
d'acqua, o pure in un pozzo, capace di poco più che la mole di detta colonna,
nell'alzarla ed estrarla dell'acqua, secondo che la colonna si sollevasse, l'acqua, che la
circonda, s'andrebbe abbassando; e l'abbassamento dell'acqua allo spazio dell'alzamento
della colonna avrebbe la medesima proporzione, che la grossezza della colonna all'eccesso
della larghezza del pozzo o vivaio sopra la grossezza di essa colonna: sì che, se il
pozzo fusse l'ottava parte più largo della grossezza della colonna, e la larghezza del
vivaio venticinque volte maggiore della medesima grossezza, nell'alzar che si facesse la
colonna un braccio, l'acqua del pozzo s'abbasserebbe sette braccia, e quella del vivaio un
ventiquattresimo di braccio solamente. Sia
nel vaso, qual si è detto, collocato il prisma ACDB, e nel resto dello spazio
infusa l'acqua, sino al livello EA; e alzandosi il solido AD, sia trasferito
in GM, e l'acqua s'abbassi da EA in NO: dico che la scesa dell'acqua,
misurata dalla linea AO, alla salita del prisma, misurata dalla linea GA, ha
la stessa proporzione, che la base del solido GH alla superficie dell'acqua NO.
Il che è manifesto: perché la mole del solido GABH, alzata sopra 'l primo livello
EAB, è eguale alla mole dell'acqua, che si è abbassata, ENOA: son dunque
due prismi eguali, ENOA e GABH: ma de' prismi eguali le base rispondono
contrariamente alle altezze: adunque, come l'altezza OA all'altezza AG,
così è la superficie o base GH alla superficie dell'acqua NO. Quando
dunque, per esemplo, una colonna fusse collocata in piede in un grandissimo vivaio pieno
d'acqua, o pure in un pozzo, capace di poco più che la mole di detta colonna,
nell'alzarla ed estrarla dell'acqua, secondo che la colonna si sollevasse, l'acqua, che la
circonda, s'andrebbe abbassando; e l'abbassamento dell'acqua allo spazio dell'alzamento
della colonna avrebbe la medesima proporzione, che la grossezza della colonna all'eccesso
della larghezza del pozzo o vivaio sopra la grossezza di essa colonna: sì che, se il
pozzo fusse l'ottava parte più largo della grossezza della colonna, e la larghezza del
vivaio venticinque volte maggiore della medesima grossezza, nell'alzar che si facesse la
colonna un braccio, l'acqua del pozzo s'abbasserebbe sette braccia, e quella del vivaio un
ventiquattresimo di braccio solamente.
Dimostrato questo, non sarà difficile lo 'ntendere, per la sua vera cagione, come un
prisma o cilindro retto, di materia in ispecie men grave dell'acqua, se sarà circondato
dall'acqua secondo tutta la sua altezza, non resterà sotto, ma si solleverà, benché
l'acqua circunfusa fosse pochissima e di gravità assoluta quanto si voglia inferiore alla
gravità di esso prisma.
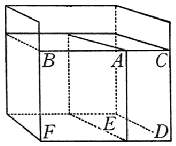 Sia
dunque nel vaso CDFB posto il prisma AEFB, men grave in ispecie dell'acqua,
e, infusa l'acqua, alzisi sino all'altezza del prisma: dico che lasciato il prisma in sua
libertà, si solleverà, sospinto dall'acqua circunfusa CDEA. Imperocché, essendo
l'acqua CE più grave in ispecie del solido AF, maggior proporzione avrà il
peso assoluto dell'acqua CE al peso assoluto del prisma AF che la mole CE
alla mole AF (imperocché la stessa proporzione ha la mole alla mole, che il peso
assoluto al peso assoluto, quando le moli sono della medesima gravità in ispecie): ma la
mole CE alla mole AF ha la medesima proporzione, che la superficie
dell'acqua CA alla superficie o base del prisma AB, la quale è la medesima
che la proporzione dell'alzamento del prisma, quando si elevasse, all'abbassamento
dell'acqua circunfusa CE: adunque il peso assoluto dell'acqua CE al peso
assoluto del prisma AF ha maggior proporzione, che l'alzamento del prisma AF
all'abbassamento di essa acqua CE. Il momento, dunque, composto della gravità
assoluta dell'acqua CE e della velocità del suo abbassamento, mentre ella fa
forza, premendo, di scacciare e di sollevare il solido AF, è maggiore del momento
composto del peso assoluto del prisma AF e della tardità del suo alzamento, col
qual momento egli contrasta allo scacciamento e forza fattagli dal momento dell'acqua:
sarà dunque sollevato il prisma. Sia
dunque nel vaso CDFB posto il prisma AEFB, men grave in ispecie dell'acqua,
e, infusa l'acqua, alzisi sino all'altezza del prisma: dico che lasciato il prisma in sua
libertà, si solleverà, sospinto dall'acqua circunfusa CDEA. Imperocché, essendo
l'acqua CE più grave in ispecie del solido AF, maggior proporzione avrà il
peso assoluto dell'acqua CE al peso assoluto del prisma AF che la mole CE
alla mole AF (imperocché la stessa proporzione ha la mole alla mole, che il peso
assoluto al peso assoluto, quando le moli sono della medesima gravità in ispecie): ma la
mole CE alla mole AF ha la medesima proporzione, che la superficie
dell'acqua CA alla superficie o base del prisma AB, la quale è la medesima
che la proporzione dell'alzamento del prisma, quando si elevasse, all'abbassamento
dell'acqua circunfusa CE: adunque il peso assoluto dell'acqua CE al peso
assoluto del prisma AF ha maggior proporzione, che l'alzamento del prisma AF
all'abbassamento di essa acqua CE. Il momento, dunque, composto della gravità
assoluta dell'acqua CE e della velocità del suo abbassamento, mentre ella fa
forza, premendo, di scacciare e di sollevare il solido AF, è maggiore del momento
composto del peso assoluto del prisma AF e della tardità del suo alzamento, col
qual momento egli contrasta allo scacciamento e forza fattagli dal momento dell'acqua:
sarà dunque sollevato il prisma.
Séguita ora che procediamo avanti a dimostrare più particolarmente, sino a quanto
saranno tali solidi, men gravi dell'acqua, sollevati, cioè qual parte di loro resterà
sommersa, e quale sopra la superficie dell'acqua. Ma prima è necessario dimostrare il
seguente lemma.
I pesi assoluti de' solidi hanno la proporzion composta delle proporzioni delle lor
gravità in specie e delle lor moli.
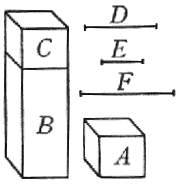 Sieno
due solidi A e B: dico, il peso assoluto di A al peso assoluto di B
aver la proporzion composta delle proporzioni della gravità in ispecie di A alla
gravità in ispecie di B e della mole A alla mole B. Abbia la linea D
alla E la medesima proporzione che la gravità in ispecie di A alla gravità
in ispecie di B, e la E alla F sia come la mole A alla mole B;
è manifesto, la proporzione D ad F esser composta delle proporzioni D
ad E ed E ad F: bisogna dunque dimostrare, come D ad F,
così essere il peso assoluto di A al peso assoluto di B. Pongasi il solido C
eguale ad A in mole, e della medesima gravità in ispecie del solido B:
perché dunque A e C sono in mole eguali, il peso assoluto di A al
peso assoluto di C avrà la medesima proporzione che la gravità in ispecie di A
alla gravità in ispecie di C o di B, che è in ispecie la medesima, cioè
che la linea D alla E: e perché C e B sono della medesima
gravità in ispecie, sarà come il peso assoluto di C al peso assoluto di B,
così la mole C, o vero la mole A, alla mole B, cioè la linea E
alla F. Come dunque il peso assoluto di A al peso assoluto di C,
così la linea D alla E, e come il peso assoluto di C al peso
assoluto di B, così la linea E alla F: adunque, per la proporzione
eguale, il peso assoluto di A al peso assoluto di B è come la linea D
alla linea F: che bisognava dimostrare. Sieno
due solidi A e B: dico, il peso assoluto di A al peso assoluto di B
aver la proporzion composta delle proporzioni della gravità in ispecie di A alla
gravità in ispecie di B e della mole A alla mole B. Abbia la linea D
alla E la medesima proporzione che la gravità in ispecie di A alla gravità
in ispecie di B, e la E alla F sia come la mole A alla mole B;
è manifesto, la proporzione D ad F esser composta delle proporzioni D
ad E ed E ad F: bisogna dunque dimostrare, come D ad F,
così essere il peso assoluto di A al peso assoluto di B. Pongasi il solido C
eguale ad A in mole, e della medesima gravità in ispecie del solido B:
perché dunque A e C sono in mole eguali, il peso assoluto di A al
peso assoluto di C avrà la medesima proporzione che la gravità in ispecie di A
alla gravità in ispecie di C o di B, che è in ispecie la medesima, cioè
che la linea D alla E: e perché C e B sono della medesima
gravità in ispecie, sarà come il peso assoluto di C al peso assoluto di B,
così la mole C, o vero la mole A, alla mole B, cioè la linea E
alla F. Come dunque il peso assoluto di A al peso assoluto di C,
così la linea D alla E, e come il peso assoluto di C al peso
assoluto di B, così la linea E alla F: adunque, per la proporzione
eguale, il peso assoluto di A al peso assoluto di B è come la linea D
alla linea F: che bisognava dimostrare.
Passo ora a dimostrar come: Se un cilindro o prisma solido sarà men grave in ispecie
dell'acqua, posto in un vaso come di sopra, di qual si voglia grandezza, e infusa poi
l'acqua, resterà il solido senza essere sollevato sin che l'acqua arrivi a tal parte
dell'altezza di quello, alla quale tutta l'altezza del prisma abbia la medesima
proporzione che la gravità in ispecie dell'acqua alla gravità in ispecie di esso solido;
ma infondendo più acqua, il solido si solleverà.
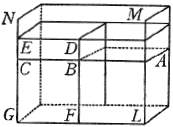 Sia
il vaso MLGN, di qualunque grandezza, ed in esso sia collocato il prisma solido DFGE,
men grave in ispecie dell'acqua; e qual proporzione ha la gravità in ispecie dell'acqua a
quella del prisma, tale abbia l'altezza DF all'altezza FB: dico che,
infondendosi acqua sino all'altezza FB, il solido DG non si eleverà, ma ben
sarà ridotto all'equilibrio, sì che ogni poco più d'acqua che si aggiunga, si
solleverà. Sia dunque infusa l'acqua sino al livello ABC; e perché la gravità in
ispecie del solido DG alla gravità in ispecie dell'acqua è come l'altezza BF
all'altezza FD, cioè come la mole BG alla mole GD, e la proporzione
della mole BG alla mole GD con la proporzione della mole GD alla mole
AF compongono la proporzione della mole BG alla mole AF, adunque la
mole BG alla mole AF ha la proporzion composta delle proporzioni della
gravità in ispecie del solido GD alla gravità in ispecie dell'acqua e della mole GD
alla mole AF. Ma le medesime proporzioni, della gravità in ispecie di GD
alla gravità in ispecie dell'acqua, e della mole GD alla mole AF,
compongono ancora, per lo lemma precedente, la proporzione del peso assoluto del solido DG
al peso assoluto della mole dell'acqua AF: adunque, come la mole BG alla
mole AF, così è il peso assoluto del solido DG al peso assoluto della mole
dell'acqua AF. Ma come la mole BG alla mole AF, così è la base del
prisma DE alla superficie dell'acqua AB, e così la scesa dell'acqua AB
alla salita del solido DG: adunque la scesa dell'acqua alla salita del prisma ha la
medesima proporzione, che il peso assoluto del prisma al peso assoluto dell'acqua; adunque
il momento resultante dalla gravità assoluta dell'acqua AF e dalla velocità del
moto nell'abbassarsi, col qual momento ella fa forza per cacciare e sollevare il prisma DG,
è eguale al momento che risulta dalla gravità assoluta del prisma DG e dalla
velocità del moto con la quale, sollevato, ascenderebbe; col qual momento e' resiste
all'essere alzato: perché dunque tali momenti sono eguali, si farà l'equilibrio tra
l'acqua e 'l solido. Ed è manifesto che, aggiugnendo un poco d'acqua sopra l'altra AF,
s'accrescerà gravità e momento, onde il prisma DG sarà superato e alzato, sin
che la sola parte BF resti sommersa: che è quello che bisognava dimostrare. Sia
il vaso MLGN, di qualunque grandezza, ed in esso sia collocato il prisma solido DFGE,
men grave in ispecie dell'acqua; e qual proporzione ha la gravità in ispecie dell'acqua a
quella del prisma, tale abbia l'altezza DF all'altezza FB: dico che,
infondendosi acqua sino all'altezza FB, il solido DG non si eleverà, ma ben
sarà ridotto all'equilibrio, sì che ogni poco più d'acqua che si aggiunga, si
solleverà. Sia dunque infusa l'acqua sino al livello ABC; e perché la gravità in
ispecie del solido DG alla gravità in ispecie dell'acqua è come l'altezza BF
all'altezza FD, cioè come la mole BG alla mole GD, e la proporzione
della mole BG alla mole GD con la proporzione della mole GD alla mole
AF compongono la proporzione della mole BG alla mole AF, adunque la
mole BG alla mole AF ha la proporzion composta delle proporzioni della
gravità in ispecie del solido GD alla gravità in ispecie dell'acqua e della mole GD
alla mole AF. Ma le medesime proporzioni, della gravità in ispecie di GD
alla gravità in ispecie dell'acqua, e della mole GD alla mole AF,
compongono ancora, per lo lemma precedente, la proporzione del peso assoluto del solido DG
al peso assoluto della mole dell'acqua AF: adunque, come la mole BG alla
mole AF, così è il peso assoluto del solido DG al peso assoluto della mole
dell'acqua AF. Ma come la mole BG alla mole AF, così è la base del
prisma DE alla superficie dell'acqua AB, e così la scesa dell'acqua AB
alla salita del solido DG: adunque la scesa dell'acqua alla salita del prisma ha la
medesima proporzione, che il peso assoluto del prisma al peso assoluto dell'acqua; adunque
il momento resultante dalla gravità assoluta dell'acqua AF e dalla velocità del
moto nell'abbassarsi, col qual momento ella fa forza per cacciare e sollevare il prisma DG,
è eguale al momento che risulta dalla gravità assoluta del prisma DG e dalla
velocità del moto con la quale, sollevato, ascenderebbe; col qual momento e' resiste
all'essere alzato: perché dunque tali momenti sono eguali, si farà l'equilibrio tra
l'acqua e 'l solido. Ed è manifesto che, aggiugnendo un poco d'acqua sopra l'altra AF,
s'accrescerà gravità e momento, onde il prisma DG sarà superato e alzato, sin
che la sola parte BF resti sommersa: che è quello che bisognava dimostrare.
Da quanto si è dimostrato si fa manifesto, come i solidi men gravi in ispecie
dell'acqua si sommergono solamente sin tanto, che tanta acqua in mole quanta è la parte
del solido sommersa pesi assolutamente quanto tutto il solido. Imperocché, essendosi
posto che la gravità in ispecie dell'acqua alla gravità in ispecie del prisma DG
abbia la medesima proporzione che l'altezza DF all'altezza FB, cioè che il
solido DG al solido GB, dimostrerremo agevolmente, che tanta acqua in mole
quanta è la mole del solido BG, pesa assolutamente quanto tutto il solido DG.
Imperocché, per lo lemma precedente, il peso assoluto d'una mole d'acqua eguale alla mole
BG, al peso assoluto del prisma DG ha la proporzione composta delle
proporzioni della mole BG alla mole GD e della gravità in ispecie
dell'acqua alla gravità in ispecie del prisma: ma la gravità in ispecie dell'acqua, alla
gravità in ispecie del prisma è posta come la mole DG alla mole GB:
adunque la gravità assoluta d'una mole d'acqua uguale alla mole BG, alla gravità
assoluta del solido GD ha la proporzione composta delle proporzioni della mole BG
alla mole GD e della mole DG alla mole GB, che è proporzione
d'egualità. La gravità, dunque, assoluta d'una mole d'acqua eguale alla parte della mole
del prisma BG, è eguale alla gravità assoluta di tutto 'l solido DG.
 Séguita
in oltre che, posto un solido men grave dell'acqua in un vaso di qual si voglia grandezza,
e circunfusagli attorno acqua sino a tale altezza, che tanta acqua in mole, quanta sia la
parte del solido sommersa, pesi assolutamente quanto tutto il solido, egli da tale acqua
sarà giustamente sostenuto, e sia l'acqua circunfusa in quantità immensa o
pochissima. Imperocchè, se il cilindro o prisma M, men grave dell'acqua, v.
g., in proporzione subsesquiterza, sarà posto nel vaso immenso ABCD, e alzatagli
attorno l'acqua sino a' tre quarti della sua altezza, cioè sino al livello AD,
sarà sostenuto e equilibrato per appunto: lo stesso gli accadrebbe se il vaso ENSF
fusse piccolissimo, in modo che tra 'l vaso e 'l solido M restasse uno angustissimo
spazio, e solamente capace di tanta acqua che né anche fusse la centesima parte della
mole M, dalla quale egli similmente sarebbe sollevato e retto, come prima ella
fusse alzata sino alli tre quarti dell'altezza del solido. Il che a molti potrebbe, nel
primo aspetto, aver sembianza di grandissimo paradosso, e destar concetto che la
dimostrazione di tale effetto fosse sofistica e fallace; ma per quelli che per tale la
reputassero, c'è la sperienza di mezo, che potrà rendergli certi: ma chi sarà capace di
quanto importi la velocità del moto, e come ella a capello ricompensa il difetto e 'l
mancamento di gravità, cesserà di maravigliarsi, nel considerare come all'alzamento del
solido M pochissimo s'abbassa la gran mole dell'acqua ABCD, ma assaissimo ed
in uno stante decresce la piccolissima mole dell'acqua ENSF come prima il solido M
si eleva, benché per brevissimo spazio; onde il momento composto della poca gravità
assoluta dell'acqua ENSF e della grandissima velocità nello abbassarsi, pareggia
la forza e 'l momento che risulta dalla composizione dell'immensa gravità dell'acqua ABCD
con la grandissima tardità nell'abbassarsi, avvegna che, nell'alzarsi il solido M,
l'abbassamento della pochissima acqua ES si muove tanto più velocemente che la
grandissima mole dell'acqua AC, quanto appunto questa è più di quella. Il che
dimostrerremo così. Séguita
in oltre che, posto un solido men grave dell'acqua in un vaso di qual si voglia grandezza,
e circunfusagli attorno acqua sino a tale altezza, che tanta acqua in mole, quanta sia la
parte del solido sommersa, pesi assolutamente quanto tutto il solido, egli da tale acqua
sarà giustamente sostenuto, e sia l'acqua circunfusa in quantità immensa o
pochissima. Imperocchè, se il cilindro o prisma M, men grave dell'acqua, v.
g., in proporzione subsesquiterza, sarà posto nel vaso immenso ABCD, e alzatagli
attorno l'acqua sino a' tre quarti della sua altezza, cioè sino al livello AD,
sarà sostenuto e equilibrato per appunto: lo stesso gli accadrebbe se il vaso ENSF
fusse piccolissimo, in modo che tra 'l vaso e 'l solido M restasse uno angustissimo
spazio, e solamente capace di tanta acqua che né anche fusse la centesima parte della
mole M, dalla quale egli similmente sarebbe sollevato e retto, come prima ella
fusse alzata sino alli tre quarti dell'altezza del solido. Il che a molti potrebbe, nel
primo aspetto, aver sembianza di grandissimo paradosso, e destar concetto che la
dimostrazione di tale effetto fosse sofistica e fallace; ma per quelli che per tale la
reputassero, c'è la sperienza di mezo, che potrà rendergli certi: ma chi sarà capace di
quanto importi la velocità del moto, e come ella a capello ricompensa il difetto e 'l
mancamento di gravità, cesserà di maravigliarsi, nel considerare come all'alzamento del
solido M pochissimo s'abbassa la gran mole dell'acqua ABCD, ma assaissimo ed
in uno stante decresce la piccolissima mole dell'acqua ENSF come prima il solido M
si eleva, benché per brevissimo spazio; onde il momento composto della poca gravità
assoluta dell'acqua ENSF e della grandissima velocità nello abbassarsi, pareggia
la forza e 'l momento che risulta dalla composizione dell'immensa gravità dell'acqua ABCD
con la grandissima tardità nell'abbassarsi, avvegna che, nell'alzarsi il solido M,
l'abbassamento della pochissima acqua ES si muove tanto più velocemente che la
grandissima mole dell'acqua AC, quanto appunto questa è più di quella. Il che
dimostrerremo così.
Nel sollevarsi il solido M, l'alzamento suo all'abbassamento dell'acqua ENSF
circunfusa ha la medesima proporzione, che la superficie di essa acqua alla superficie o
base di esso solido M; la qual base alla superficie dell'acqua AD ha la
proporzion medesima, che l'abbassamento dell'acqua AC all'alzamento del solido M;
adunque, per la proporzion perturbata, nell'alzarsi il medesimo solido M,
l'abbassamento dell'acqua ABCD all'abbassamento dell'acqua ENSF ha la
medesima proporzione, che la superficie dell'acqua EF alla superficie dell'acqua AD,
cioè che tutta la mole dell'acqua ENSF a tutta la mole ABCD, essendo
egualmente alte. È manifesto, dunque, come nel cacciamento e alzamento del solido M
l'acqua ENSF supera in velocità di moto l'acqua ABCD di tanto, di quanto
ella vien superata da quella in quantità: onde i momenti loro in tale operazione son
ragguagliati.
 |
 |
E per amplissima
confermazione... |
|
|