 |
Galileo Galilei
Intorno alle cose che stanno in su l'acqua o che in quella si muovonoQuarta pagina |
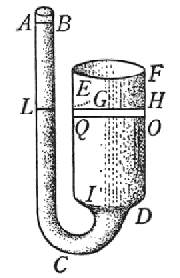 E per amplissima confermazione e più chiara esplicazione di questo medesimo,
considerisi la presente figura (e, s'io non m'inganno, potrà servire per cavar
d'errore alcuni meccanici prattici, che sopra un falso fondamento tentano talora imprese
impossibili), nella quale al vaso larghissimo EIDF, vien continuata l'angustissima
canna ICAB, ed intendasi in essi infusa l'acqua sino al livello LGH; la
quale in questo stato si quieterà, non senza meraviglia di alcuno, che non capirà così
subito come esser possa, che il grave carico della gran mole dell'acqua GD,
premendo abbasso, non sollevi e scacci la piccola quantità dell'altra contenuta dentro
alla canna CL, dalla quale gli vien contesa ed impedita la scesa. Ma tal meraviglia
cesserà, se noi cominceremo a fingere l'acqua GD essersi abbassata solamente sino
a QO, e considereremo poi ciò che averà fatto l'acqua CL. la quale, per
dar luogo all'altra che si è scemata dal livello GH sino al livello QO,
doverà per necessità essersi nell'istesso tempo alzata dal livello L sino in AB,
ed esser la salita LB tanto maggiore della scesa GQ, quant'è l'ampiezza del
vaso GD maggiore della larghezza della canna LC, che in somma è quanto
l'acqua GD è più della LC. Ma essendo che il momento della velocità del
moto in un mobile compensa quello della gravità di un altro, qual meraviglia sarà se la
velocissima salita della poca acqua CL resisterà alla tardissima scesa della molta
GD? E per amplissima confermazione e più chiara esplicazione di questo medesimo,
considerisi la presente figura (e, s'io non m'inganno, potrà servire per cavar
d'errore alcuni meccanici prattici, che sopra un falso fondamento tentano talora imprese
impossibili), nella quale al vaso larghissimo EIDF, vien continuata l'angustissima
canna ICAB, ed intendasi in essi infusa l'acqua sino al livello LGH; la
quale in questo stato si quieterà, non senza meraviglia di alcuno, che non capirà così
subito come esser possa, che il grave carico della gran mole dell'acqua GD,
premendo abbasso, non sollevi e scacci la piccola quantità dell'altra contenuta dentro
alla canna CL, dalla quale gli vien contesa ed impedita la scesa. Ma tal meraviglia
cesserà, se noi cominceremo a fingere l'acqua GD essersi abbassata solamente sino
a QO, e considereremo poi ciò che averà fatto l'acqua CL. la quale, per
dar luogo all'altra che si è scemata dal livello GH sino al livello QO,
doverà per necessità essersi nell'istesso tempo alzata dal livello L sino in AB,
ed esser la salita LB tanto maggiore della scesa GQ, quant'è l'ampiezza del
vaso GD maggiore della larghezza della canna LC, che in somma è quanto
l'acqua GD è più della LC. Ma essendo che il momento della velocità del
moto in un mobile compensa quello della gravità di un altro, qual meraviglia sarà se la
velocissima salita della poca acqua CL resisterà alla tardissima scesa della molta
GD?
Accade, adunque, in questa operazione lo stesso a capello che nella stadera, nella
quale un peso di due libre ne contrappeserà un altro di 200, tuttavolta che nel tempo
medesimo quello si dovesse muovere per ispazio 100 volte maggiore che questo; il che
accade quando l'un braccio della libra sia più cento volte lungo dell'altro. Cessi per
tanto la falsa opinione in quelli che stimavano che un navilio meglio e più agevolmente
fosse sostenuto in grandissima copia d'acqua che in minor quantità (fu ciò creduto da
Aristotile ne' Problemi, alla Sezion 23, Probl. 2), essendo, all'incontro, vero che è
possibile che una nave così ben galleggi in dieci botti di acqua come nell'oceano.
Ma, seguitando la nostra materia, dico che da quanto si è sin qui dimostrato possiamo
intendere, come uno de' soprannominati solidi, quando fusse più grave in ispecie
dell'acqua, non potrebbe mai da qualsivoglia quantità di quella esser sostenuto. Imperò
che, avendo noi veduto, come il momento, col quale un tal solido grave in ispecie come
l'acqua contrasta col momento di qualunque mole d'acqua, è potente a ritenerlo sino alla
total sommersione, senza che egli si elevi; resta manifesto, che molto meno potrà
dall'acqua esser sollevato, quando e' sia più di quella grave in ispecie: onde,
infondendosi acqua sino alla total sua sommersione, resterà ancora in fondo, e con tanta
gravità e renitenza all'esser sollevato, quanto è l'eccesso del suo peso assoluto sopra
il peso assoluto d'una mole a sé eguale fatta d'acqua o di materia in ispecie egualmente
grave come l'acqua. E benché s'aggiugnesse poi grandissima quantità d'acqua sopra il
livello di quella che pareggia l'altezza del solido, non però s'accresce la pressione o
aggravamento delle parti circonfuse al detto solido, per la quale maggior pressione egli
avesse ad esser cacciato; perché il contrasto non gli vien fatto se non da quelle parti
dell'acqua, le quali al moto d'esso solido esse ancora si muovono, e queste son quelle
solamente che son comprese tra le due superficie equidistanti all'orizzonte e fra di loro
parallele, le quali comprendon l'altezza del solido immerso nell'acqua.
Parmi d'aver sin qui a bastanza dichiarata e aperta la strada alla contemplazione della
vera, intrinseca e propria cagione de' diversi movimenti e della quiete de' diversi corpi
solidi ne' diversi mezi e in particolare nell'acqua, mostrando come in effetto il tutto
depende dagli scambievoli eccessi della gravità de' mobili e de' mezi, e, quello che
sommamente importava, rimovendo l'instanza ch'a molti avrebbe potuto per avventura
apportar gran dubbio e difficultà intorn'alla verità della mia conclusione, cioè come,
stante che l'eccesso della gravità dell'acqua sopra la gravità del solido, che in essa
si pone, sia cagion del suo galleggiare e sollevarsi dal fondo alla superficie, possa una
quantità d'acqua, che pesi meno di dieci libre, sollevare un solido che pesi più di
cento: dove abbiamo dimostrato, come basta che tali differenze si trovino tra le gravità
in ispecie de' mezi e de' mobili, e sien poi le gravità particolari e assolute quali
esser si vogliano; in guisa tale che un solido, purch'ei sia in ispezie men grave
dell'acqua, benché poi di peso assoluto fosse mille libre, potrà da dieci libre d'acqua,
e meno, essere innalzato; e, all'opposito, altro solido, purché in ispecie sia più grave
dell'acqua, benché di peso assoluto non fosse più d'una libbra, non potrà da tutto 'l
mare esser sollevato dal fondo o sostenuto. Questo mi basta, per quanto appartiene al
presente negozio, avere co' sopra dichiarati esempli scoperto e dimostrato, senza estender
tal materia più oltre e, come si potrebbe, in lungo trattato; anzi, se non fosse stata la
necessità di risolvere il sopra posto dubbio, mi sarei fermato in quello solamente che da
Archimede vien dimostrato nel primo libro Delle cose che stanno sopra l'acqua,
dov'in universale si concludono e stabiliscon le medesime conclusioni, cioè che i solidi
men gravi dell'acqua soprannuotano, i più gravi vanno al fondo, gli egualmente gravi
stanno indifferentemente in ogni luogo, purché stieno totalmente sotto acqua.
Ma perché tal dottrina d'Archimede, vista, trascritta ed esaminata dal Sig. Francesco
Buonamico nel quinto libro Del moto, al cap. 29, e poi dal medesimo confutata,
potrebbe dall'autorità di filosofo così celebre e famoso esser resa dubbia e sospetta di
falsità; ho giudicato necessario 'l difenderla, se sarò potente a farlo, e purgare
Archimede da quelle colpe delle quali par ch'e' venga imputato.
Lascia il Buonamico la dottrina d'Archimede, prima, come non concorde con l'opinion
d'Aristotile; soggiugnendo, parergli cosa ammiranda che l'acqua debba superar la terra in
gravità, vedendosi, in contrario, crescer la gravità nell'acqua mediante la
participazion della terra. Soggiugne appresso, non restar soddisfatto delle ragioni
d'Archimede, per non poter con quella dottrina assegnar la cagione, donde avvenga che un
legno e un vaso, che per altro stia a galla nell'acqua, vada poi al fondo se s'empierà
d'acqua; che, per essere il peso dell'acqua, che in esso si contiene, eguale
all'altr'acqua, dovrebbe fermarsi al sommo nella superficie; tuttavia si vede andare in
fondo. Di più aggiugne che Aristotile chiaramente ha confutato gli antichi, che dicevano
i corpi leggieri esser mossi all'in su, scacciati dalla 'mpulsione dell'ambiente più
grave; il che se fusse, parrebbe che di necessità ne seguisse, che tutti i corpi naturali
fussero di sua natura gravi e niuno leggiere, perché 'l medesimo accadrebbe ancora
dell'aria e del fuoco, posti nel fondo dell'acqua. E benché Aristotile conceda la
pulsione negli elementi, per la quale la terra si riduce in figura sferica, non però, per
suo parere, è tale che ella possa rimuovere i corpi gravi dal luogo suo naturale; anzi
che più tosto gli manda verso il centro, al quale (come egli alquanto oscuramente
séguita di dire) principalmente si muove l'acqua, se già ella non incontra chi gli
resista e per la sua gravità non si lasci scacciare dal luogo suo, nel qual caso, se non
direttamente, al meno come si può, conseguisce il centro: ma al tutto per accidente i
leggieri per tale impulsione vengono ad alto, ma ciò hanno per lor natura, come anche lo
stare a galla. Conclude finalmente di convenir con Archimede nelle conclusioni, ma non
nelle cause, le quali egli vuol riferire alla facile o difficile divisione del mezo, e al
dominio degli elementi: sì che quando il mobile supera la podestà del mezo, come, per
esempio, il piombo la continuità dell'acqua, si moverà per quella; altramente, no.
Questo è quello che io ho potuto raccorre, esser prodotto contro Archimede dal Sig.
Buonamico: il quale non s'è curato d'atterrare i principii e le supposizioni d'Archimede,
che pure è forza che sieno falsi, se falsa è la dottrina da quelli dependente; ma s'è
contentato di produrre alcuni inconvenienti e alcune repugnanze all'opinione e alla
dottrina d'Aristotile. Alle quali obbiezioni rispondendo dico, prima, che l'essere
semplicemente la dottrina d'Archimede discorde da quella d'Aristotile, non dovrebbe
muovere alcuno ad averla per sospetta, non constando cagion veruna per la quale
l'autorità di questo debba essere anteposta all'autorità di quello. Ma perché, dove
s'hanno i decreti della natura, indifferentemente esposti a gli occhi dello intelletto di
ciascheduno, l'autorità di questo e di quello perde ogni autorità nel persuadere,
restando la podestà assoluta alla ragione; però passo a quello che vien nel secondo
luogo prodotto, come assurdo conseguente alla dottrina d'Archimede, cioè che l'acqua
dovesse esser più grave della terra. Ma io veramente non trovo che Archimede abbia detta
tal cosa, né che ella si possa dedurre dalle sue conclusioni; e quando ciò mi fusse
manifestato, credo assolutamente che io lascerei la sua dottrina, come falsissima. Forse
è appoggiata questa deduzione del Buonamico sopra quello che egli soggiugne del vaso, il
quale galleggia sin che sarà vòto d'acqua, ma poi, ripieno, va al fondo; e intendendo
d'un vaso di terra, inferisce contro Archimede così: Tu di' che i solidi che galleggiano,
sono men gravi dell'acqua; questo vaso di terra galleggia; adunque tal vaso è men grave
dell'acqua, e però la terra è men grave dell'acqua. Se tale è la illazione, io
facilmente rispondo, concedendo che tal vaso sia men grave dell'acqua, e negando l'altra
conseguenza, cioè che la terra sia men grave dell'acqua. Il vaso che soprannuota, occupa
nell'acqua non solamente un luogo eguale alla mole della terra della quale egli è
formato, ma eguale alla terra e all'aria insieme nella sua concavità contenuta; e se una
tal mole, composta di terra e d'aria, sarà men grave d'altrettanta acqua, soprannoterà,
e sarà conforme alla dottrina d'Archimede: ma se poi, rimovendo l'aria, si riempierà il
vaso d'acqua, sì che il solido posto nell'acqua non sia altro che terra, né occupi altro
luogo che quello che dalla sola terra viene ingombrato, allora egli andrà al fondo, per
esser la terra più grave dell'acqua; e ciò concorda benissimo con la mente d'Archimede.
Ecco il medesimo effetto dichiarato con altra esperienza simile. Nel volere spignere al
fondo una boccia di vetro mentre è ripiena d'aria, si sente grandissima renitenza,
perché non è il solo vetro quello che si spigne sotto acqua, ma, insieme col vetro, una
gran mole d'aria, e tale che chi prendesse tanta acqua quanta è la mole del vetro e
dell'aria in esso contenuta, avrebbe un peso molto maggiore che quello della boccia e
della sua aria; e però non si sommergerà senza gran violenza: ma se si metterà
nell'acqua il vetro solamente, che sarà quando la boccia s'empierà d'acqua, allora il
vetro discenderà al fondo, come superiore in gravità all'acqua.
Tornando, dunque, al primo proposito, dico che la terra è più grave dell'acqua, e che
però un solido di terra va al fondo; ma può ben farsi un composto di terra e d'aria, il
quale sia men grave d'altrettanta mole di acqua, e questo resterà a galla: e sarà l'una
e l'altra esperienza molto ben concorde alla dottrina d'Archimede. Ma perché ciò mi pare
che non abbia difficultà, io non voglio affermativamente dire che il Sig. Buonamico
volesse da un simil discorso opporre ad Archimede l'assurdo, dello 'nferirsi dalla sua
dottrina che la terra fusse men grave dell'acqua; benché io veramente non sappia
immaginarmi, quale altro accidente lo possa avere indotto a ciò.
 |
 |
Forse tal problema... |
|
|