Sviluppi ulteriori
Equivalenza massa-energia
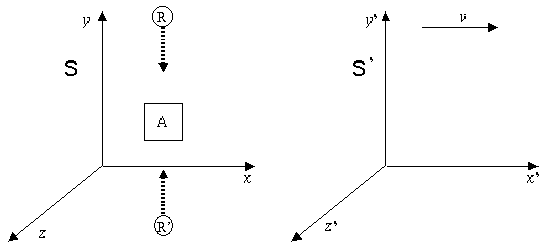
Si consideri il corpo libero A, in quiete rispetto ad S. Due impulsi di radiazione R e R', ciascuna di energia E/2, si muovono rispettivamente nella direzione positiva e negativa dell'asse y e vengono infine assorbite da A.
L'energia di A aumenta di un valore E ed A rimane in quiete in S per ragioni di simmetria. Come sarà visto lo stesso fenomeno in S'? I due impulsi di radiazione viaggiano, rispetto ad S', in direzioni che individuano con l'asse y' un angolo dato dalla legge dell'aberrazione della luce
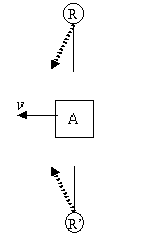
e che in prima approssimazione
vale: 
.
Dalle considerazioni svolte a proposito di S, si ottiene che la velocità v di A resta immutata dopo l'assorbimento di R e R'.
Un risultato della teoria dell'elettromagnetismo di Maxwell è che una radiazione di energia E possiede una quantità di moto pari a E/c. Nel nostro caso quindi ciascun impulso di radiazione possiede una quantità di moto pari a E/(2c). Rigorosamente parlando, questo è il suo valore rispetto a S; tuttavia, supponendo v piccola rispetto a c, la quantità di moto rispetto ad S' è la stessa. La sua componente secondo l'asse x è:
ovvero, con sufficiente precisione:
.
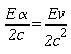Perciò R e R' insieme posseggono una quantità di moto Ev/c2 nella direzione dell'asse x. La quantità di moto totale del sistema prima dell'assorbimento è quindi:
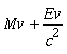
Dopo l'assorbimento sia M' la massa di A. A questo punto si deve prevedere la possibilità che la massa sia aumentata a causa dell'assorbimento di energia E. La quantità di moto del sistema dopo l'assorbimento è allora: M'v . La legge di conservazione della quantità di moto applicata rispetto alla direzione dell'asse x conduce all'equazione:
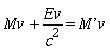, o anche: 
.
Questa equazione esprime la legge di equivalenza fra la massa e l'energia. L'aumento di energia E è legato all'aumento di massa E/c2 . Dato che l'energia, in base alla sua definizione usuale, è determinata a meno di una costante additiva, possiamo scegliere questa in modo che sia:
.
(A.Einstein, Pensieri degli Anni Difficili, ed. Boringhieri)
