Conseguenze delle trasformazioni
Invarianza dell'intervallo spazio-temporale
Come si è visto le trasformazioni di Lorentz implicano la variazione degli intervalli spaziali e temporali nel passare da un sistema di riferimento all'altro. Esiste però, ed è sempre conseguenza dell'invarianza di c, una grandezza invariante, combinazione dei suddetti intervalli che viene chiamato intervallo o distanza spazio-temporale.
Dati due eventi descritti dalle coordinate (x1,y 1,z1,t1) e (x2,y2,z2,t 2) nel sistema S, il quadrato della loro distanza spazio-temporale è definito come:
![]()
con l'ovvio significato delle variazioni delle coordinate. Se ora si vuole calcolare il quadrato dell'intervallo nel sistema S' basta tener presente che si ha:
![]()
![]()
![]()
![]()
E' un semplice esercizio di algebra mostare allora che il quadrato dell'intervallo è invariante, cioè che si ottiene:
![]()
Tale grandezza è utile per calcolare il tempo proprio di un punto, il tempo cioè misurato da un orologio che si muove solidalmente al punto: in tale riferimento infatti lo spostamento spaziale è nullo e quindi si ottiene:
![]()
Ciò vale se il punto si muove di moto uniforme; se invece si ha un moto vario, questo si può pensare come una successione di moto uniformi che durano intervalli infinitesimi ed il tempo proprio sarà dato da:
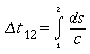
Il moto di un punto nello spazio-tempo si suole descrivere mediante la cosiddetta linea universo , una linea che rappresenta in uno spazio quadridimensionale le coordinate che caratterizzano il moto del punto. Per semplicità di rappresentazione, conviene pensare ad un moto che avviene in una dimensione spaziale (asse orizzontale) al passare del tempo (asse verticale); un esempio di linea universo è allora:

La linea tratteggiata rappresenta la propagazione di un raggio di luce: è evidente che la pendenza della linea universo non può mai essere inferiore a quella di una linea luce, perchè ciò significherebbe una velocità maggiore di c.