Precedente Indice Successivo



Pmq2


Scopo: calcolo dei coefficienti del polinomio dei minimi quadrati di 2° grado
Specifiche: subroutine pmq2 (x, y, n, c, r, ifail)
integer n, ifail
real x(n), y(n), c(3), r(n)
Descrizione: Backgroud del problema

La determinazione del polinomio di minimi quadrati di 2° grado si particolarizza nella risoluzione del seguente sistema:

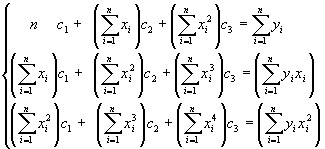
la cui soluzione fornisce i coefficienti (c1,c2, c3) del polinomio c1+c2x+c3 x2 che realizza l'approssimazione ottimale.

Descrizione dell'algoritmo

La risoluzione del sistema normale B*c=d, essendo la matrice B simmetrica e definita positiva, può avvenire mediante la fattorizzazione di Cholesky B=L*Lt (richiamando la subroutine chol) e la risoluzione dei due sistemi:

L * w = d
Lt * c = w
(richiamando le subroutine fsbpk e bsbpk). Determinati i coefficienti, si calcolano infine i residui.

Raccomandazioni sull'uso

Il numero dei punti deve essere maggiore di tre. Se è pari il problema si riduce ad un'interpolazione, e l'uso di tale subroutine è sconsigliato perché fornisce i coefficienti in modo meno efficiente ed accurata rispetto alla subroutine conwt. Le ascisse non devono essere tutte uguali.

Bibliografia: [1], [2]
Parametri di I/O: input

x - vettore di reali, ascisse dei punti
y - vettore di reali, ordinate dei punti
n - intero, numero di punti inseriti
c - vettore di reali, coefficienti del polinomio

output

r - vettore di reali, residui
ifail - intero, indicatore d'errore
Indicatori d'errore: Errori gestiti dalla subroutine:
ifail =  0 nessun errore.
ifail = 11 il numero dei punti è non positivo.
ifail = 13 il numero di punti pari è a 1 o 2 o le ascisse sono tutte uguali.
ifail = 14 subroutine inadeguata al problema.
Routines ausiliarie: Chol, procedura, fattorizzazione di Cholesky
Fsbpk, procedura, forward substitution per matrici formato packed
Bsbpk, procedura, backward substitution per matrici formato packed
Tempo d'esecuzione: la complessità asintotica è O(n3/6).
Memoria richiesta: sono allocati 3 array di dimensione n.
Accuratezza fornita: metodo esatto a meno del condizionamento della matrice dei coefficienti del sistema normale e degli errori di round-off.
Esempio di programma chiamante: 
      Program pmq2d
      
c     Programma dimostrativo della subroutine pmq2.
      
      external pmq2
      
      integer dim
      parameter (dim=100)
      
      real x(dim),y(dim),r(dim),c(3)
      integer ifail
      character*12 fin,fout
            
      print*
      print*,'*** PROGRAMMA DIMOSTRATIVO DELLA SUBROUTINE PMQ2 ***'
      print*
      write(*,*)'Numero di nodi (max',dim,')= '
      read(*,*)n
      
      print*,'Nome del file di input= '
      read(*,'(A)')fin
      open(11,FILE=fin,STATUS='OLD')
      do 1 i=1,n
         read(11,*)x(i)
    1 continue
      do 2 i=1,n
         read(11,*)y(i)
    2 continue 
      close(11)
            
      call pmq2(x,y,n,c,r,ifail)
       
      if (ifail .eq. 11) stop 'Errore! numero di punti non valido'
      if (ifail .eq. 13) stop 'Errore! infinite soluzioni'
      if (ifail .eq. 14) print*,'Attenzione! algoritmo inadeguato'
            
      print*,'Nome del file di output= '
      read(*,'(A)')fout
      open(12,FILE=fout)
      write(12,'(E14.7)')(c(i),i=1,3)
      write(12,*)
      write(12,'(E14.7)') (r(i),i=1,n)
      close(12)
      
      write(*,10)'Coefficiente del termine di grado 0: ',c(1)
      write(*,10)'Coefficiente del termine di grado 1: ',c(2)
      write(*,10)'Coefficiente del termine di grado 2: ',c(3)
            
      print*,'Residuo= '
      write(*,'(E14.7)')(r(i),i=1,n)
               
   10 format (1X,A,E14.7)
   
      End



Precedente Indice Successivo