Precedente Indice Successivo



Fft2


Scopo: calcolo della Trasformata Discreta di Fourier (DFT) "radix-2" o della sua inversa (IDFT)
Specifiche: subroutine fft2( flag, f, n, ifail)
logical flag
integer n, ifail
complex f(n)
Descrizione: Backgroud del problema

Posto wn=e2p i/n ed assegnati n numeri complessi f0, f1, f2,...,fn-1 bisogna calcolare gli n numeri complessi F0, F1, F2,..., Fn-1 con:

il vettore


è detto Trasformata Discreta di Fourier (DFT) del vettore
mentre il vettore
con:
è detto Trasformata Discreta Inversa di Fourier (IDFT) del vettore

Descrizione dell'algoritmo

L'algoritmo è una implementazione della Fast Fourier Transform (FFT) radix-2, che consente di ricondurre il calcolo di una DFT di ordine n (potenza di 2) al calcolo di più DFT di ordine 2 mediante l'algoritmo FFT. Rappresentati in binario gli indici j e k:   j = 2 m-1p0+2m-2p1+...+2pm-2 +pm-1
k = 2m-1q0+2m-2q1+...+2qm-2 +qm-1 con pi, qi = {0,1}, m=log2(n) e con i = 0,...,m-1, risulta che:

che si ottiene esprimendo la (6.1) in funzione della rappresentazione binaria degli indici j e k. In generale al passo m-esimo dell'algoritmo si ha:
con:
e ciascun vettore Cm è costruito ricorsivamente calcolando n/2 DFT di ordine 2. All'ultimo passo il vettore Cm e il vettore
avranno le stesse componenti, ma in ordine inverso, queste componenti saranno poi ordinate con una operazione di "bit-reversal" che opera sulla rappresentazione binaria dell'indice dei vettori.

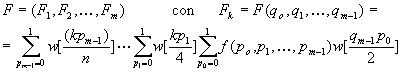
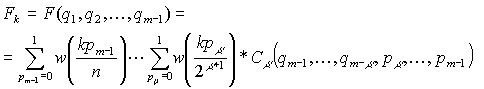
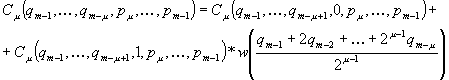
Raccomandazioni sull'uso

L'algoritmo consente di calcolare sia la trasformata sia la sua inversa, mediante un flag che deve essere settato ad 1 per il calcolo della FFT, a 0 per calcolare l'inversa IDFT. Oltre al programma chiamante va collegata la funzione bitrev, che effettua il bit-reversal degli ultimi k bit della rappresentazione binaria di un numero intero.

Poiché l'algoritmo è in grado di gestire esclusivamente DFT a base 2, è necessario accertarsi che il numero di punti che si inseriscono sia una potenza di due e che tali numeri siano rappresentati in notazione complessa "(a+jb)", anche qualora essi siano dei reali (uguagliando a zero la parte immaginaria). Dato che l'algoritmo, per ridurre la complessità di spazio lavora in place, il vettore f che in ingresso conteneva i numeri complessi su cui lavorare, in uscita conterrà il vettore trasformato.

Bibliografia: [1], [2], [5], [6]
Parametri di I/O: input

f - vettore di complessi, vettore da trasformare
n - intero, ordine trasformata.
flag - booleano, scelta tra fft e ifdt

output

f - vettore di complessi, trasformata
Indicatori d'errore: Errori gestiti dalla subroutine:
ifail = 0 nessun errore. ifail = 1 un ordine della trasformata inserito è non positivo ifail = 2 l'ordine della trasformata inserito non è una potenza di 2
Routines ausiliarie: bitrev, funzione intera, esegue il bit-reversal, degli ultimi k bit della rappresentazione binaria di un numero intero.
Tempo d'esecuzione: la complessità di tempo è O(Nlog2N)
Memoria richiesta: un solo array allocato, contenente le componenti del vettore da trasformare o antitrasformare.
Accuratezza fornita: metodo esatto a meno di errori di round-off.
Esempio di programma chiamante: 
      Program fft2d
c     Programma dimostrativo della subroutine fft2 
 
      external fft2
      
      integer nmax
      parameter(nmax=32)
      
      integer n,ifail
      real x(nmax),y(nmax)
      complex f(nmax)
      character*12 fin,fout1,fout2

      print*,'*** PROGRAMMA DIMOSTRATIVO DELLA SUBROUTINE FFT2 ***'
      print*
      write(*,20)'Ordine della trasformata (max ',nmax,')= '
      read(*,*)n
      print*
      print*,'Nome del file di input= '
      read(*,'(A)')fin
      open(11,FILE=fin,STATUS='OLD')
      do 1 i=1,n
         read(11,*)x(i)
    1 continue
      read(11,*)
      do 2 i=1,n
         read(11,*)y(i)
    2 continue 
      close(11)                  
c     Costruzione del vettore di numeri complessi      
      do 10 i=1,n
         f(i)=cmplx(x(i),y(i))
   10 continue

c     Trasformata       
      call fft2(1,f,n,ifail)

      if (ifail .eq. 20) stop 'Errore! ordine non valido'
      if (ifail .eq. 21) stop 'Errore! l''ordine non è potenza di due'
      
      print*
      print*,'Nome del file di output (DFT)= '
      read(*,'(A)')fout1
      open(12,FILE=fout1)
      write(12,'(2E14.7)')(f(i),i=1,n)
      close(12)

      print*,'Vettore trasformato= '
      write(*,30)(real(f(i)),aimag(f(i)),i=1,n)
                  
c     Antitrasformata
      call fft2(0,f,n,ifail)
      
      print*
      print*,'Nome del file di output (IDFT)= '
      read(*,'(A)')fout2
      open(13,FILE=fout2)
      write(13,'(2E14.7)')(f(i),i=1,n)
      close(13)

      print*,'Vettore antitrasformato='
      write(*,30)(real(f(i)),aimag(f(i)),i=1,n)
                  
   20 format(1X,A,I2,A)
   30 format(1X,'(',E13.7,',',E14.7,')')
      
      End



Precedente Indice Successivo