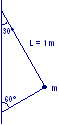Fisica

Costanti Fisiche

Unità Misura

Esercizi Fisica

Applet Java

Quesiti

      Forze, lavoro, energia                                            

Esercizio n. 1

Una forza applicata ad un corpo puntiforme di massa    m = 0,175 kg    lo fa passare da una velocità     v₁ = 10 cm/s    ad una velocità v₂ = 98 cm/s.

Calcolare il lavoro compiuto dalla forza.

Se il moto è rettilineo e la forza applicata ha la stessa direzione della traiettoria del corpo ed un modulo di 1 N, calcolare lo spazio ed il tempo in cui si ha la variazione di velocità suddetta.

R.: 0,083 J ; 8,3 cm ; 0,15 s

Esercizio n. 2

Una forza costante F = 7,48 N è applicata ad un punto materiale.

Questo si sposta di s = 48 cm in una direzione formante un angolo di 35° con quello della forza.

Trovare il lavoro compiuto dalla forza.

Se si vuole che la forza, provocando lo stesso spostamento s, compia il lavoro L = 2 J , quanto deve valere l’angolo?

Se il punto materiale ha massa 444 g e inizialmente è fermo, quale velocità ha acquistato dopo lo spostamento s?

R.: 2,94 J ; 56,15° ; 3,6 m/s ;

Esercizio n. 3

Un tronco dal peso di 1000 N è tirato a velocità costante di 1,2 m/s con una forza di 400 N per mezzo di una fune lunga 1,5 m.

La distanza tra l’estremo della fune ed il suolo è 80 cm.

Trovare il coefficiente di attrito dinamico tra il tronco ed il suolo.

Calcolare il lavoro eseguito dalla forza durante un intervallo di tempo di 15 minuti.

R.: 0,43 ; 370 KJ

Esercizio n. 4

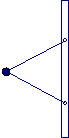
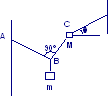
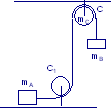
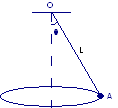
Una sfera di 1 kg è fissata ad un’asta rigida verticale mediante due fili di massa trascurabile di lunghezza 1 m.

I fili sono fissati all’asta in due punti distanti 1 m.

Il sistema ruota intorno all’asta con entrambi i fili tesi e formanti un triangolo equilatero con l’asta.

La tensione del filo superiore è 25 N.

Calcolare la tensione del filo inferiore, la forza risultante sulla sfera e la velocità della sfera.

R.: 5,4 N ; 26,3 N ; 4,78 m/s ;

Esercizio n. 5

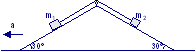
Due corpi di massa m₁ = 1,5 kg e m₂ = 3 kg , fissati agli estremi di un’asta di massa trascurabile si muovono su di un piano inclinato verso il basso  ed m₁ segue la pista di m₂.

L’angolo di inclinazione è 30°. Il coefficiente di attrito dinamico tra m₁ ed il piano inclinato è 0,3 e tra m₂ ed il piano è 0,15.

Calcolare l’accelerazione comune dei due corpi, la tensione dell’asta,  l’energia  dissipata  per  attrito  quando il sistema è scivolato di  20 cm.

R.: 3,2 m/s² ; 1,3 N ; 1,5 J ;

Esercizio n. 6

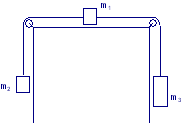
Due corpi di massa m₁ = 5,00 kg ed m₂ = 10,0 kg, collegati da una corda inestensibile di massa trascurabile, sono tirati verticalmente verso l’alto da un montacarichi elettrico che sviluppa una forza F di 300 N.

Calcolare l’accelerazione del sistema e la tensione della corda tra i due corpi.

R.: 10,2 m/s² ; 200 N ;

Esercizio n. 7

Due corpi di massa m₁ = 5,00 kg e m₂ = 10,0 kg, collegati da una fune inestensibile di massa trascurabile, sono tirati verticalmente verso il basso da una forza F di 30,0 N.

Calcolare l’accelerazione del sistema e la tensione della fune tra i due corpi.

Per quale valore di F la tensione è nulla?

R.: 11,8 m/s² ; 10,0 N ; 0 ;

Esercizio n. 8

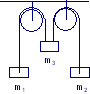
Tre blocchi sono collegati da una fune e poggiano su un tavolo orizzontale senza attrito.

Essi sono tirati orizzontalmente verso destra con una forza T₃ = 60 N.

Se m₁ = 10 kg , m₂ = 20 kg e m₃ = 30 kg , trovare l’accelerazione dei blocchi e le tensioni T₁ e T₂.

Calcolare le stesse quantità se il sistema dei blocchi non è più poggiato su di un tavolo ed è tirato verticalmente verso l’alto.

R.: 1 m/s² ; 10 N ; 30 N ; 8,81 m/s² ; 10 N ; 30 N ;

Esercizio n. 9

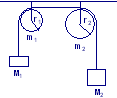
Due blocchi di massa m₁ = 3,50 kg e m₂ = 8,00 kg sono collegati tramite una fune priva di massa che passa attraverso una puleggia priva di attrito. I piani inclinati sono senza attrito. Trovare:

a)  Il modulo dell’accelerazione di ciascun blocco.

b)  La tensione della fune.

R.: 2,20 m/s² ; 27,4 N ;

Esercizio n. 10

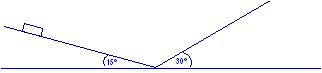
Un corpo parte da fermo e percorre 1,5 m per giungere ai piedi di un piano inclinato senza attrito e con un angolo di inclinazione di 15°. Calcolare la velocità del corpo ai piedi del piano inclinato.

Successivamente il corpo risale su di un secondo piano inclinato di pendenza 30° e coefficiente di attrito cinematico 0,2.

Calcolare la massima altezza raggiunta.

R.: 2,76 m/s ; 0,29 m ;

Esercizio n. 11

Consideriamo un ascensore che si muove verticalmente con una accelerazione di 0,5 m/s².

Un passeggero di 70 kg è nell’ascensore.

Determinare il suo peso apparente (cioè la forza esercitata sul passeggero dal pavimento):

a)  Se l’accelerazione è diretta verso l’alto.

b)  Se l’accelerazione è diretta verso il basso.

R.: 721 N ; 651 N ;

Esercizio n. 12

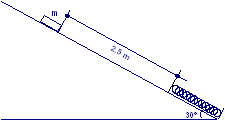
Un corpo di massa 3 kg è posto su un piano inclinato (φ = 30°) con coefficiente di attrito cinetico 0,2, a distanza 2,5 m da una molla, che giace sul piano inclinato, di costante elastica 200 N/m.

Calcolare la massima compressione della molla se il corpo parte da fermo.

Calcolare la massima quota a cui il corpo risale.

R.: 0,54 m ; 0,74 m ;

Esercizio n. 13

Un blocco di 6 kg è fermo su un piano orizzontale. Il coefficiente di attrito statico tra tavolo e blocco è 0,5.

Quale sarà l’intensità della forza orizzontale che comincia a far muovere il blocco?

Qual è la massima intensità che deve avere una forza che agisca verso il basso in direzione di 60° sull’orizzontale senza mettere in moto il blocco?

Qual è la massima intensità che deve avere una forza che agisca a 60° verso l’alto per dare lo stesso risultato?

R.: 30 N ; 448 N ; 32 N ;

Esercizio n. 14

Il cavo di un ascensore di massa 1500 kg si spezza quando l’ascensore è fermo ad una distanza d = 5 m da una molla di costante elastica k = 11,7·10⁴ N/m.

Un dispositivo di sicurezza agisce sulle guide in modo da sviluppare una forza di attrito costante di 9000 N, che si oppone al moto dell’ascensore.

Calcolare:

a)  La velocità dell’ascensore quando colpisce la molla se il dispositivo di sicurezza non entra in funzione

b)  La stessa velocità se il dispositivo entra in funzione

c)  La massima compressione della molla

d)  Di quanto risale l’ascensore la prima volta

R.: 9,9 m/s ; 6,2 m/s ; 0,75 m ; 1,4 m ;

Esercizio n. 15

Una forza orizzontale di 60 N spinge un blocco di massa 2,5 kg contro una parete verticale.

Il coefficiente di attrito statico tra la parete ed il blocco è 0,6 ed il coefficiente di attrito dinamico è 0,4.

Supponiamo che il blocco sia inizialmente fermo.

Il blocco comincerà a muoversi?

Calcolare la forza esercitata sul blocco dalla parete.

R.: no ; 65 N ; 22,6° ;

Esercizio n. 16

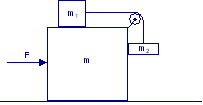
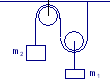
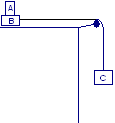
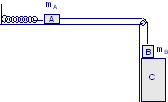
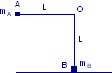
Un blocco di massa m = 10 kg poggia su di un piano senza attrito.

Due corpi di massa m₁ = 2 kg ed m₂ = 1 kg sono collegati al blocco come in figura (la fune è ideale e gli attriti sono assenti).

Calcolare il valore della forza F affinché il blocco venga spostato lungo il piano, senza che i due corpi scivolino rispetto ad esso.

R.: 63,7 N ;

Esercizio n. 17

Due blocchi di massa m₁ = 3,50 kg e m₂ = 8,00 kg sono collegati tramite una fune priva di massa che passa attraverso una puleggia priva di attrito. I coefficienti di attrito dinamico tra i blocchi e ciascun piano inclinato siano uguali.

Nella ipotesi che il sistema abbia un’accelerazione di modulo 1,50 m/s², trovare:

a)  Il valore del coefficiente di attrito dinamico.

b)  La tensione della fune.

R.: 0,0875 ; 27,4 N ;

Esercizio n. 18

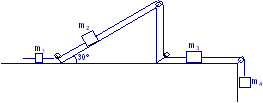
Nella situazione di figura in cui il piano inclinato forma con l’orizzontale un angolo di 30° ed i valori delle masse risultano essere

m₁ = 2 kg , m₂ = 4 kg , m₃ = 3 kg , si trovi la massa m₄ tale che m₄ abbia un’accelerazione:

a)  Verso il basso pari a g/2.

b)  Verso l’alto pari a g/4.

R.:13 kg ; 0,2 kg ;

Esercizio n. 19

Due masse m₁ = 2 kg e m₂ = 3 kg sono poggiate su di un piano orizzontale legate con una fune inestensibile e sono tirate con una forza F (applicata ad m₁) a velocità costante v = 1,5 m/s.

Il coefficiente di attrito dinamico tra la massa m₁ ed il piano vale μ_ad1 = 0,2 e tra la massa m₂ ed il piano vale μ_ad2 = 0,4. Calcolare:

a)  Il valore di F.

b)  La forza esercitata su m₂ mediante la fune.

c)  La potenza di chi tira.

d)  L’accelerazione del sistema se chi tira raddoppia la forza.

R.: 15,7 N ; 11,8 N ; 23,5 W ; 3,1 m/s² ;

Esercizio n. 20

Un blocco A di massa 4 kg è posto sopra un blocco B di 5 kg.

Per far sì che il corpo A scivoli su quello B, deve essere applicata una forza di 12 N al blocco A.

Supponendo che il piano su cui è posto B sia senza attrito, trovare la massima forza orizzontale che deve essere applicata a B perché i blocchi si muovano insieme. Calcolare l’accelerazione dei due blocchi.

R.: 27 N ; 3 m/s² ;

Esercizio n. 21

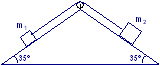
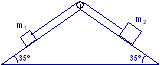
Tre blocchi m₁ = 10 kg , m₂ = 5 kg ed m₃ = 3 kg sono connessi da fili che passano su pulegge prive di attrito.

L’accelerazione comune dei tre blocchi è 2 m/s² e la superficie è scabra.

Trovare il coefficiente di attrito cinetico tra i blocchi e la superficie assumendo che sia lo stesso per i blocchi m₂ ed m₃ e la tensione nei fili. (θ = 25°)

R.: 0,66 ; 78 N ; 35,7 N ;

Esercizio n. 22

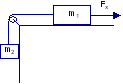
Due masse m ed M sono collegate da fili; l’angolo tra i fili che sostengono m è 90°.

Calcolare l’angolo θ all’equilibrio.

R.: 1+ 2M/m :

Esercizio n. 23

Nel sistema mostrato in figura una forza orizzontale di modulo F_x agisce su un oggetto di massa m₁. La superficie orizzontale è priva di attrito.

a)  Per quali valori di F_x l’oggetto di massa m₂ accelera verso l’alto?

b)  Per quali valori di F_x l’oggetto di massa m₂ accelera verso il basso?

c)  Per quali valori di F_x la tensione della fune è zero?

d)  Disegnare poi il grafico dell’accelerazione dell’oggetto m₁ in funzione di F_x.

R.: F_x > m₂∙g ; F_x < m₂∙g ; F_x < –m₁∙g ;

Esercizio n. 24

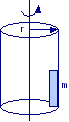
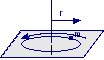
Un cilindro verticale, privo di fondo, ruota intorno al suo asse.

Qual è il massimo periodo di rotazione del cilindro T affinché una massa m rimanga bloccata contro la parete, supposto che il coefficiente di attrito statico tra la massa e la parete sia μ_s e che il raggio del cilindro sia r.

Esercizio n. 25

Una massa m, inizialmente ferma, viene spinta per una distanza d , lungo un pavimento orizzontale scabro con forza costante orizzontale F. Se il coefficiente di attrito tra cassa e pavimento è μ_a , determinare:

a)  Il lavoro compiuto dalla forza applicata F.

b)  L’energia dissipata per attrito.

c)  Il lavoro compiuto dalla forza F nella direzione della normale.

d)  Il lavoro compiuto dalla forza di gravità.

e)  La velocità finale della cassa.

f)  Eseguire i calcoli con i seguenti valori: m = 40 kg, d = 5 m, F = 130N, μa = 0,300.

R.: 650 J ; 588 J ; 0 J ; 0 J ; 1,76 m/s ;

Esercizio n. 26

Una massa m viene tirata in salita lungo un piano inclinato scabro, formante un angolo θ rispetto all’orizzontale, con una velocità iniziale v_i . La forza applicata F è parallela al piano inclinato, il coefficiente di attrito dinamico vale μ_ad e la massa viene tirata per una distanza d. Determinare:

a)  Quanto lavoro viene compiuto dalla forza di gravità.

b)  Quanta energia si dissipa per attrito.

c)  Quanto lavoro viene svolto dalla forza F.

d)  Di quanto varia l’energia cinetica della cassa.

e)  Qual è la velocità della massa dopo essere stata tirata per la distanza d.

f)   Calcolare le domande precedenti utilizzando i seguenti valori: m = 10 kg, θ = 20°, v_i = 1,50 m/s, F = 100 N, μ_ad = 0,400,

     d = 5,00 m.

R.: –168 J : –184 J ; 500 J ; 148 J ; 5,65 m/s ;

Esercizio n. 27

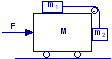
Quale forza orizzontale deve essere applicata al carrello di figura affinché i blocchi rimangano fermi relativamente al carrello?

Si assuma che tutte le superfici, ruote e pulegge siano prive di attrito.

Esercizio n. 28

Due masse sono collegate con un filo inestensibile come in figura. Il filo passa su una carrucola liscia.

Si trovi l’accelerazione di ciascuna massa e la tensione nel filo per m₁ = 200 g ed m₂ = 100 g.

R.: 3,3 m/s² ; 1,3 N ;

Esercizio n. 29

Calcolare l’accelerazione dei corpi m₁ ed m₂ e la tensione delle funi. Tutte le carrucole sono senza peso e senza attrito.

Quale dei sistemi illustrati può accelerare m₁ più che in caduta libera?

Risolvere il problema dapprima algebricamente, lo si applichi poi al caso in cui m₁ = 4 kg e m₂ = 6 kg.

R.: 5,34 m/s² ; 2,67 m/s² ; 21,36 N ; 4,20 m/s² ; 8,40 m/s² ; 16,80 N ;

Esercizio n. 30

Le masse di A e di B in figura sono rispettivamente di 10 kg e di 5 kg. Il coefficiente di attrito tra A ed il tavolo è 0,20.

Trovare la minima massa di C necessaria per impedire il movimento di A.

Si calcoli l’accelerazione del sistema quando C viene sollevato.

R.: 15 kg ; g/5 ;

Esercizio n. 31

Calcolare l’accelerazione dei corpi in figura e la tensione del filo.

Risolvere dapprima il problema algebricamente ed applicarlo al caso in cui m₁ = 50 g, m₂ = 80 g ed F = 10⁵ dine = 1 N.

R.: 166 cm/s² ; 9,17·10⁴ dine ; 543 cm/s² ; 1,22·10⁵ dine ;

Esercizio n. 32

I corpi di figura sono collegati da un filo inestensibile come in figura.

Supponendo che le carrucole siano lisce, calcolare l’accelerazione dei corpi e la tensione del filo.

Risolvere il problema dapprima algebricamente ed applicarlo poi al caso in cui m₁ = 8 kg ed m₂ = 2 kg.

R.:  2,45 m/s² ; 4,90 m/s² ; 29,42 N ;  58,84 N ; 

Esercizio n. 33

Dato il sistema di masse (m₁ = m₂ = 1 kg , m₃ = 2 kg), funi e carrucole mostrato in figura, determinare l’accelerazione con cui si muove la massa m₃ e la tensione delle funi, trascurando l’attrito tra la massa m₁ e il piano.

R.: a = g/4 = 2.45m/s² ; T₂ = 12.25 N ; T₃ = 14.70 N ;

Esercizio n. 34

Determinare l’accelerazione della massa m₃ e la tensione delle due funi nel sistema di masse, funi e carrucole mostrato in figura, dove

m₁ = m₂ = m₃ = 1 kg.

R.: a = g/3 = 3.27 m/s² ; T₁ = T₂ = 6.53 N ;

Esercizio n. 35

Nel sistema in figura le carrucole, di massa e raggio rispettivamente  m₁ = 3 kg, r₁ = 10 cm , m₂ = 6 kg , r₂ = 15 cm, sono ad asse fisso e la corda, inestensibile e senza massa, non slitta su di esse.

Calcolare i vettori accelerazione dei due corpi di massa M₁ = 1 kg ed M₂ = 2 kg, i vettori accelerazione angolare delle due carrucole e le tensioni nei vari tratti di corda.

R.: 1,31 m/s² ; 13,2 rad/s² ; 8,71 rad/s² ; 11,1 N ; 17,0 N ; 13,1 N ;

Esercizio n. 36

Del sistema in figura si calcoli il valore massimo che può avere la massa B perchè il sistema risulti in equilibrio. Per m_B pari al doppio del valore di cui al precedente punto si calcolino l’accelerazione del sistema e le tensioni nei diversi tratti delle funi.

Si considerino le funi inestensibili, flessibili e prive di massa e la carrucola C₁ priva di massa.

Si assumano per le altre masse i seguenti valori m_A = 1 kg , m_C = 0,5 kg.

Si assuma il coefficiente di attrito statico tra il piano orizzontale ed il corpo A pari a 0,35 e quello di attrito dinamico pari a 0,32.

Si assuma g = 10 m/s².

R.: 0,35 kg ; 1,95 m/s² ; 5,64 N ; 5,15 N ;

Esercizio n. 37

Due blocchetti A e B di massa 2 kg e 4 kg sono sovrapposti e poggiano sopra un piano con coefficiente di attrito cinetico 0,1; una corda, passante per una carrucola fissa collega il corpo B ad un corpo C sospeso; il coefficiente di attrito statico tra i due blocchetti è 0,5.

Se la massa del corpo C è 5 kg, i blocchi A e B si muovono insieme; calcolare la loro accelerazione e la forza di attrito tra i due blocchi.

Calcolare il valore massimo della massa del corpo C affinché A non scivoli indietro.

R.: 3,92 m/s² ; 7,84 N ; 7,2 kg ;

Esercizio n. 38

I coefficienti di attrito cinetico tra i due blocchi e tra il blocco inferiore ed il piano orizzontale è 0,25.

Sapendo che la forza applicata F è 30 N, calcolare l’accelerazione dei due corpi e la tensione della fune.

Dati m₁ = 2 kg e m₂ = 3 kg.

R.: 1,59 m/s² ; 21,9 N ;

Esercizio n. 39

Una barca è trainata da due cavalli, posti ciascuno su una sponda del fiume.

I cavalli percorrono due sentieri paralleli al filo della corrente (rettilineo) ma posti a distanze diverse dalle sponde.

Il cavallo percorrente il sentiero più vicino al fiume produce un tiro nella fune paria a F₁ = 80 N  e precede la barca in modo che la fune formi un angolo α = 30° con il filo della corrente.

La R resistenza offerta dalla corrente stessa al moto della barca è di R = 160 N.

La larghezza del fiume è L = 20 m , le distanze a e b dei due sentieri paralleli alla relativa sponda valgono a = 2 m e b = 8 m.

Si vuole che la barca, essendo priva di timone, percorra l’asse della corrente.

Quale sforzo F₂ dovrà esercitare lungo la propria fune il secondo cavallo e di quanto esso dovrà procedere indietro o avanti rispetto al primo.

R.: 99 N ; 20 m ;

Esercizio n. 40

Si osserva che un corpo di massa m₁ = 5 kg posto su una parete verticale di un carrello di massa M = 70 kg che è tirato da una forza costante F, scende con velocità costante rispetto al carrello. Sapendo che il coefficiente di attrito tra la parete ed il corpo è μ_a = 0,7 , calcolare:

a)  La forza di attrito.

b)  La risultante delle forze agenti sul corpo.

c)  L’accelerazione del carrello.

d)  La forza F (trascurando l’attrito tra le ruote del carrello ed il suolo).

R.: 49 N ; 70 N ; 14 m/s² ; 1050 N ;

Esercizio n. 41

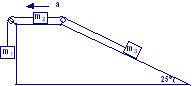
Sulla coppia di piani inclinati (angolo di inclinazione 30°), che si spostano orizzontalmente verso sinistra con accelerazione a = 1,5 m/s² , scivolano due corpi di massa m₁ = 6 kg ed m₂ = 2 kg , collegati tra loro mediante una corda ed attraverso una carrucola fissa.

Calcolare l’accelerazione dei corpi relativamente al piano inclinato e le reazioni dei piani inclinati.

R.: 1,15 m/s2 ; 55,5 N ; 15,5 N ;

R.: 1,15 m/s² ; 55,5 N ; 15,5 N ;

Esercizio n. 42

Un corpo A di massa m_A = 3 kg è collegato da una parte ad una parete con una molla di costante elastica f = 60 N/m e dall’altra ad un corpo B di massa m_B = 1,5 Kg con una fune inestensibile passante per una carrucola fissa.

Inizialmente il sistema dei due corpi è in quiete con la molla nella condizione di riposo ed il corpo B è sostenuto da un corpo C.

Si toglie il corpo C lasciando i corpi A e B liberi. Calcolare:

a)  L’allungamento massimo della molla.

b)  La tensione della fune e l’accelerazione dei due corpi in tale posizione (corrispondente al massimo allungamento).

R.: 0,49 m ; 19,6 m ; 3,3 m/s² ;

Esercizio n. 43

Un uomo di massa m = 75 kg in corsa con velocità v = 1,5 m/s, salta su un carrello inizialmente fermo. Se la massa del carrello è 

M = 120 kg calcolare la velocità del sistema uomo-carrello dopo il salto, supponendo che l’uomo sia fermo rispetto al carrello.

R.: 0,58 m/s ;

Esercizio n. 44

Un ragazzo di massa m = 45 kg sta su una tavola che ha una massa M = 150 kg .

La tavola, inizialmente ferma, è libera di scivolare su un lago ghiacciato, che è un piano con la superficie di appoggio senza attrito. Il ragazzo comincia a camminare lungo la tavola ad una velocità costante v_{ragazzo-tavola} = 1,5 m/s relativamente alla tavola.

a)  Qual è la velocità del ragazzo relativamente alla superficie del ghiaccio?

b)  Qual è la velocità della tavola relativa alla superficie del ghiaccio?

R.: 1,15 m/s ; – 0,35 m/s ;

Esercizio n. 45

Due carrelli di massa m₁ = 100 kg ed m₂ = 200 kg viaggiano in direzioni opposte con velocità v₁ = 1 m/s e v₂ = 2 m/s.

Sopra il carrello m₁ vi è un uomo di massa M = 60 kg, il quale salta fuori dal carrello in direzione opposta al moto del carrello con velocità v_o = 0,5 m/s rispetto ad esso, quando i carrelli distano d = 1,5 m.

Determinare dopo quanto tempo dal salto dell’uomo i due carrelli si scontrano.

Sapendo che l’urto è perfettamente anelastico determinare la velocità finale.

R.: 0,45 s ; 0,9 m/s ;

Esercizio n. 46

Un blocco di massa m = 0,500 kg viene premuto contro una molla orizzontale, di massa trascurabile, provocandone una compressione Δx. La costante elastica della molla è k = 450 N/m. Il blocco, lasciato libero, si muove lungo un piano orizzontale, privo di attrito fino al punto B, al fondo di una guida circolare verticale scabra di raggio R = 1,00 m e continua a muoversi in su lungo la guida.

La velocità del blocco nel punto B è v_B = 12,0 m/s. Il blocco è sottoposto ad una forza media di attrito lungo il percorso circolare della guida pari a F_a = 7,00 N. Determinare:

a)  La compressione iniziale della molla.

b)  La velocità del blocco alla sommità della guida circolare, posizione T.

c)  Il blocco riuscirà a raggiungere la sommità della pista o cadrà prima?

R.: 0,4 m ; 4,1 m/s ; si ;

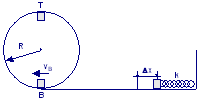
Esercizio n. 47

Un cane di massa m = 5 kg è fermo all’estremo di una zattera di massa M = 20 kg e dista d = 6 m dalla riva.

Esso cammina per l = 3 m (l , lunghezza della zattera) verso la riva e si ferma. Quanto dista il cane dalla riva ?

R.: 3,6 m ;

Esercizio n. 48

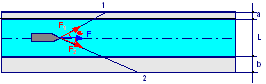
Una sferetta di massa m = 5,00 g scivola senza attrito lungo la guida mostrata in figura.

La sferetta viene lasciata andare da un’altezza h = 3,50·R.

a)  Qual è il valore della velocità della sferetta nella posizione A e quanto vale la forza che la guida deve esercitare su di essa?

b)  Qual è il valore della velocità della sferetta nella posizione B e quanto vale la forza che la guida deve esercitare su di essa?

c) Qual dovrebbe essere l’altezza minima dalla quale si dovrebbe far partire una sferetta di qualsiasi massa per percorrere interamente il circuito rappresentato in figura?

R.:

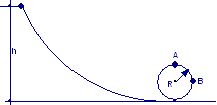
Esercizio n. 49

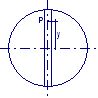
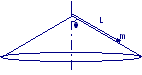
Una pallina A è legata all’estremità di un filo di lunghezza L = 24 cm, avente l’altra estremità fissa nel punto O.

La pallina viene fatta ruotare orizzontalmente lungo un cerchio.

Si calcoli la velocità della pallina lungo la sua traiettoria circolare, nel caso in cui il filo individui un angolo θ = 30° rispetto alla verticale.

R.: 0,82 m/s ;

Esercizio n. 50

I tre corpi A di massa M_A = 1 kg, B di massa M_B = 0,5 kg e C di massa M_C = 0,5 kg sono disposti su di un piano orizzontale privo di attrito come indicato in figura.

Il coefficiente di attrito statico tra A e B sia μ₁= 0,5 e quello cinetico sia μ_c1 = 0,45, tra B e C μ₂ = 0,5 e μ_c2 =0,45.

Una forza orizzontale di modulo F è applicata al corpo B. Calcolare il valore massimo di F prima che C o A inizi a strisciare rispetto a B, dire chi striscia prima. Per F = 15 N si calcolino le accelerazioni dei tre corpi.

Assumere g = 10 m/s².

R.: 10 N ; insieme ; 4,5 m/s² ; 16,5 m/s² ; 4,5 m/s² ;

Esercizio n. 51

Un piccolo blocco di massa m = 1 kg striscia su una superficie orizzontale senza attrito mentre viaggia all’interno di un cerchio di raggio  r = 0,5 m. Il coefficiente di attrito tra il blocco e la parete è μ_a = 0,2, pertanto la velocità v del blocco diminuisce.

a)  Trovare, in funzione di v, la forza di attrito sul blocco e l’accelerazione tangenziale del blocco.

b)  Calcolare il tempo necessario perché la velocità si riduca da un valore iniziale v_o = 2,5 m/s ad un valore v_o/4.

c)  Calcolare il numero di giri in tale intervallo.

R.: 0,40· v² N ; 0,40· v² m/s² ; 3 s ; 1,1 giri ;

Esercizio n. 52

Un sasso viene lasciato cadere con velocità iniziale nulla in un pozzo profondo fino al centro della terra.

Trovare la velocità del sasso quando arriva al centro della terra ed il tempo impiegato, trascurando ogni attrito e la rotazione della terra. (raggio della terra R = 6600 km)

R.: 8040 m/s ; 1209 s;

Esercizio n. 53

In un treno fermo, un punto materiale è alla base di un piano inclinato di θ = 15° rispetto all’orizzontale e lungo L = 1,2 m. All’improvviso il treno parte con accelerazione a = 5 m/s² ed il punto materiale risale tutto il piano inclinato e cade giù.

Calcolare, rispetto al treno, l’accelerazione del punto materiale lungo il piano inclinato, la sua velocità alla fine del piano inclinato e determinare la posizione in cui il punto materiale tocca il pavimento del vagone dopo la caduta.

R.: 2,29 m/s² ; 2,35 m/s ; 0,986 m ;

Esercizio n. 54

Un corpo di massa m = 12 kg, legato attraverso una fune di lunghezza L = 1,5 m, si trova su una superficie conica, la cui sezione passante per l’asse del cono forma con la verticale un angolo θ = 60°, ruota attorno all’asse del cono con la frequenza di 10 giri/min. Calcolare la velocità lineare del corpo, la reazione della superficie sul corpo, la tensione del filo e la frequenza di rotazione in giri/min necessaria per annullare la reazione della superficie.

R.: 1,36 m/s ; 93,3 N ; 73,6 N ; 34,5 giri/min ;

Esercizio n. 55

Un corpo A di massa m_A = 4 kg è collegato, tramite un filo inestensibile lungo 2·L, ad un corpo B di massa m_B= 8 kg.

Il punto di mezzo passa per una carrucola fissa.

Caso a): B è fissato su un piano orizzontale ed il filo OB è verticale, il corpo A con il filo OA teso e orizzontale viene lasciato libero con velocità iniziale nulla. Calcolare la velocità del corpo A, la tensione del filo e la reazione del vincolo sul corpo B in funzione dell’angolo formato dal filo con la verticale.

Caso b): Il corpo B non è fissato sul piano orizzontale, ma poggiato. Determinare la tensione del filo e l’angolo formato dal filo OA quando B si stacca dal piano su cui è poggiato.

Esercizio n. 56

Un corpo di massa m = 3 kg si muove senza attrito su un piano inclinato di angolo θ = 30° rispetto all’orizzontale. Sulla sommità del piano è posta una molla di costante elastica k = 200 N/m.

Se il corpo parte quando la sua distanza dall’estremo libero della molla è L = 50 cm, calcolare la velocità iniziale del corpo affinché la compressione massima della molla sia Δs = 25 cm. Supponendo, invece, il piano inclinato con coefficiente di attrito cinetico μ_ac = 0,15, calcolare la velocità iniziale che dà la stessa compressione.

R.: 3,4 m/s ; 3,7 m/s ;

Esercizio n. 57

Una sfera di massa m = 100 g è fissata ad un’asta rigida verticale mediante due fili di massa trascurabile come in figura.

Il sistema ruota attorno all’asta, con entrambi i fili tesi, alla frequenza di 2 giri al secondo.

Calcolare la tensione dei due fili. Calcolare la frequenza minima perché entrambi i fili risultino tesi.

Supponendo che la tensione di rottura dei fili sia T_rottura = 10 N, determinare la frequenza massima sopportabile.

R.: 4,80 N ; 6,35 N ; 0,54 Hz ; 2,5 Hz ;

Esercizio n. 58

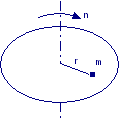
Un blocchetto di massa m è posto su una piattaforma circolare che ruota intorno ad un asse verticale compiendo n = 60 giri/min. A che distanza dall’asse di rotazione si porta il blocchetto se tra esso e la piattaforma si ha un coefficiente di attrito μ = 0,3?

R.: 7,5 cm ;

Esercizio n. 59

Un blocco di massa m = 2,00 kg è fermo sul bordo sinistro di un blocco di massa M = 8,00 kg.

Il coefficiente di attrito dinamico fra i due blocchi è μ_ad = 0,300, e la superficie sulla quale è fermo il blocco di 8,00 kg è senza attrito. Una forza orizzontale costante F = 100 N è applicata al blocco da 2,00 kg mettendolo in moto. Se la distanza L percorsa dal bordo del blocco piccolo sul blocco grande è d = 3 m calcolare:

a)  Quanto impiegherà il blocco piccolo per giungere fino al bordo destro del blocco da 8,00 kg.

b)  Quale distanza percorre il blocco da 8,00 kg in questo processo.

R.: 2,13 s ; 1,67 m ;

Esercizio n. 60

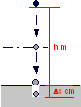
Una sferetta di massa m = 40 g viene lasciata cadere da un’altezza h = 7 m con una velocità iniziale di v₀ = 2 m/s.

Calcolare:

a)   La velocità della sferetta a metà percorso di caduta.

b)   La velocità della sferetta al suolo.

c)   Il valore della forza di attrito ed il rispettivo lavoro quando la sferetta penetra per Δx = 25 cm nella sabbia costituente il pavimento.

R.: 8,52 m/s ; 11,89 m/s ; 11,70N ; 2,95 J ;

Esercizio n. 61

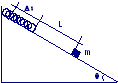
Un blocchetto è lanciato verso l'alto lungo un piano con inclinazione 15 gradi, con una velocità iniziale di v_i = 5 m/s.
Tra il blocco ed il piano vi è un coefficiente di attrito statico pari a μ_as = 0.4 ed un coefficiente di attrito dinamico pari a

μ_ad = 0.3 .
Calcolare:
a) In quanto tempo il blocchetto si ferma
b) Quanto spazio percorre il blocchetto prima di fermarsi
c) Stabilire infine se il blocchetto, una volta fermo ricomincia o meno a scendere e, in caso positivo, con quale valore di accelerazione

R.: 0,92 s ; 2,3 m ; fermo ;