Fisica

Le leggi del moto                                     

Esercizio n. 1

Due treni partono da una stazione A ad intervallo di tempo 10 min.

Il primo raggiunge la stazione B dopo un tempo di 2,5 h, viaggiando con velocità costante 100 km/h.

Quale deve essere la velocità v₂ del secondo treno affinché raggiunga B nel medesimo istante del primo treno.

R.: 30 m/s ;

Esercizio n. 2

Un punto si muove nel piano xy e la sua posizione è data dal vettore: r(t) = i · c · t  +  j · b · e ^(–kt).

Determinare la velocità e l’accelerazione.

Determinare l’equazione della traiettoria.

R.: v_x = c , v_y = – k·b·e^(–kt) , a_x = 0 , a_y = k² · b · e ^(–kt) ; y = b · e ^(–k·x/c) ;

Esercizio n. 3

Due corridori percorrono una pista circolare di raggio R = 1500 m con velocità costanti.

Quando essi si muovono nello stesso senso, il più veloce oltrepassa l’altro ogni 300 s mentre, quando si muovono in senso contrario, si incontrano ogni 80 s.

Determinare la velocità dei due corridori. 

R.: 74,6 m/s ; 43,2 m/s ;

Esercizio n. 4

Un oggetto viene lanciato verso l’alto, in direzione verticale, con una velocità iniziale v₀ incognita; il punto di partenza O si trova ad h metri dal suolo.

Dopo aver percorso uno spazio s₁, il corpo, giunto nel punto A, ricade giungendo al suolo dopo un tempo t = 16 s dalla partenza e con una velocità finale v_B = 98 m/s.

Determinare il valore di v₀ e di h.

R.: – 58,8 m ; 313,6 m ;

Esercizio n. 5

Un veicolo A si muove nella direzione a con velocità costante v_A = 20 m/s. Da un punto B, distante 50 metri dalla direzione a viene lanciato un oggetto alla velocità costante di 10 m/s in direzione b perpendicolare ad a, in modo da colpire il veicolo.

Determinare la posizione di A all’istante del lancio e i moduli delle velocità relative di ciascun mobile rispetto all’altro.

R.: 100 m ; 22,4 m/s ; 22,4 m/s ;

Esercizio n. 6

Un veicolo A si muove nella direzione a con velocità costante v_A = 20 m/s. Dal veicolo A, in movimento, viene lanciato un oggetto, alla velocità costante di 10 m/s in direzione  perpendicolare ad A in modo da colpire un punto B distante 50 metri dalla direzione a.

Determinare il percorso AB compiuto dall’oggetto, la velocità assoluta ed il tempo impiegato.

R.: 111,8 m ; 22,4 m/s ; 5 s ;

Esercizio n. 7

Dal tetto di una casa alta H = 30 m si lascia cadere una sferetta; nello stesso istante un’altra sferetta viene lanciata verticalmente in alto dal terreno sottostante con velocità iniziale v_o = 30 m/s.

Determinare a che altezza dal terreno esse si incontrano.

R.: 25,1 m ;

Esercizio n. 8

Un sasso è lanciato verso l’alto e ricade nel punto di partenza dopo 10 s. Calcolare:

La velocità iniziale.

La velocità di arrivo.

La massima quota raggiunta.

R.: 50 m/s ; 50 m/s verso il basso ; 125 m ; (assumere g = 10 m/s²) ;

Esercizio n. 9

Un pallone è lanciato verticalmente verso l’alto dal suolo con una velocità di 29,4 m/s.

Quanto tempo impiega per raggiungere il punto più alto?

Qual è la massima altezza raggiunta?

In quale istante sarà a 39,2 m sopra il suolo?

In quale istante tocca il suolo?

R.: 3 s ; 44,1 m ; 2 s e 4 s ; 6 s ;

Esercizio n. 10

Calcolare la velocità di caduta verticale di una goccia di pioggia sapendo che la sua traiettoria apparente, visualizzata dalla traccia lasciata sul finestrino di un treno che viaggia con velocità costante di 100 km/h forma un angolo di 60° con la verticale.

R.: 57,7 km/h ;

Esercizio n. 11

Un fiume scorre con velocità v_o. Una motobarca parte e nello stesso istante un tronco galleggiante transita per la posizione di partenza. La motobarca percorre 30 km nel senso della corrente impiegando 1 h e torna immediatamente indietro al punto di partenza. Durante il ritorno incrocia di nuovo il tronco dopo aver percorso 13 km.

Calcolare il modulo della velocità della motobarca, relativamente all’acqua ed il modulo della velocità del fiume rispetto all’argine ed il tempo che la motobarca impiega a compiere il tragitto di ritorno.

R.: 21,5 km ; 8,5 km/h ,1 h ; 

Esercizio n. 12

Una palla da baseball è lanciata verso un giocatore con velocità iniziale di 20 m/s e sotto un angolo di 45° con l’orizzontale.

Nell’istante in cui la palla viene lanciata, il giocatore si trova a 50 m dal lanciatore.

Con quale velocità ed in quale direzione il giocatore deve correre per afferrare la palla alla stessa altezza a cui è stata lanciata?

R.: 3,2 m/s ;

Esercizio n. 13

Un proiettile è sparato nell’aria dalla sommità di una rupe alta 180 m sopra la valle.

La sua velocità iniziale ha il modulo di 60 m/s e forma un angolo di 60° con l’orizzontale.

Calcolare il punto in cui il proiettile raggiunge il suolo. (Trascurare la resistenza dell’aria).

R.: 393 m ;

Esercizio n. 14

Un razzo è lanciato verticalmente e sale con accelerazione verticale costante di 20 m/s² per 1 minuto.

Dopo questo tempo esso continua a salire come un corpo libero.

Calcolare la massima altezza raggiunta ed il tempo totale di lancio.

R.: 110 km ; 332 s ;

Esercizio n. 15

Un’automobile può fermarsi in 10 s quando viaggia a velocità v.

Mentre viaggia a tale velocità vede un cane a distanza d sulla sua traiettoria e frena istantaneamente.

La macchina raggiunge il cane 8 s dopo ed il cane salta fuori dalla carreggiata.

Sapendo che la macchina percorre ancora 4 m oltre la posizione del cane prima di fermarsi, calcolare d.

R.: 96 m ;

Esercizio n. 16

Un bombardiere, in picchiata ad un angolo di 60° con la verticale, lascia cadere una bomba da un’altezza di 700 metri.

La bomba colpisce il suolo 5 s dopo il lancio.

Calcolare la velocità del bombardiere e lo spostamento orizzontale della bomba durante il volo.

R.: 231 m/s ; 1000 m ;

Esercizio n. 17

Un cannone, posto a 300 m di altezza, riesce a colpire un bersaglio di coordinate (150 m, 200 m) quando il suo angolo di tiro è 45°.

Calcolare il modulo della velocità del proiettile:

Alla bocca del cannone.

Quando colpisce il bersaglio.

R.: 29,7 m/s ; 53,3 m/s ;

Esercizio n. 18

Un ragazzo, in piedi a 4 m di distanza da una parete verticale, lancia una palla.

La palla è lanciata a 2 m dal suolo con velocità di 10·√2 m/s ed angolo di 45°.

Quando la palla colpisce la parete la componente x della velocità si inverte e la componente y resta invariata.

Calcolare il punto in cui la palla colpisce il suolo.

R.: 18 m ;

Esercizio n. 19

Un punto, partendo dalla quiete, si muove lungo un cerchio di raggio 10 cm con accelerazione tangenziale costante.

Trovare detta accelerazione se la sua velocità dopo 2 rivoluzioni dall’inizio del movimento è 80 cm/s.

Calcolare tale istante.

R.: 25,5 cm/s² ; 3,1 s ;

Esercizio n. 20

Un’automobile, partendo da ferma, compie in 2.00 minuti, un giro completo su una pista circolare di raggio 360 m.

Nell’ipotesi che la sua accelerazione tangenziale sia di modulo costante, calcolarne il modulo.

Calcolare inoltre i moduli della velocità e dell’accelerazione centripeta al termine del giro.

R.: 0,314 m/s² ; 37,7 m/s ; 3,95 m/s² ;

Esercizio n. 21

Calcolare la velocità e l’accelerazione di un punto della superficie terrestre a 30° latitudine nord, sapendo che il raggio terrestre è R_t = 6380 km.

R.: 402 m/s ; 2,92·10^-2 m/s² ;

Esercizio n. 22

Di quale fattore dovrebbe crescere la velocità di rotazione della terra perché per trattenere un corpo sulla terra all’equatore sia necessaria un’accelerazione pari a g.

R.: 17 ;

Esercizio n. 23

Un satellite terrestre si muove su un orbita circolare di 600 km sopra la superficie terrestre. Il periodo di rivoluzione è 98 minuti.

Calcolare l’accelerazione di gravità dell’orbita.

R.: 8 m/s² ;

Esercizio n. 24

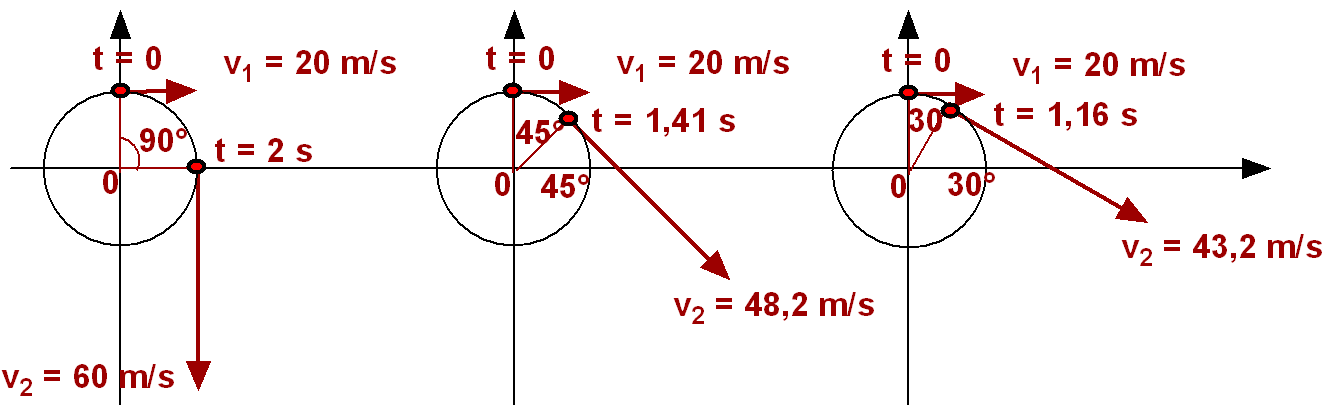
In figura delle particelle descrivono traiettorie circolari con velocità variabile in modulo. Sono indicati i vettori velocità.

Si trovi il modulo del vettore accelerazione media tra le due posizioni indicate in ciascun caso.

R.: 31,6 m/s² ; 26,2 m/s² ; 23,9 m/s² ;

Esercizio n. 25

Uno sciatore lascia la rampa di salto con una velocità di 10 m/s formante un angolo di 15° con l’orizzontale.

La discesa forma un angolo di 50° con l’orizzontale e la resistenza dell’aria è trascurabile.

Trovare la distanza alla quale atterra lo sciatore sulla discesa e le componenti della velocità all’atterraggio.

R.: 43,2 m ; 9,7 m/s e 25,6 m/s verso il basso ;

Esercizio n. 26

Un punto materiale si muove su una circonferenza di raggio 1 m con accelerazione tangenziale costante.

Trovare l'accelerazione sapendo che il vettore accelerazione forma un angolo di 60° con la direzione della velocità 2 s dopo l’inizio del moto. Il corpo parte da fermo.

R.: 0,43 m/s² ;

Esercizio n. 27

Un pendolo descrive un moto armonico con periodo T = 1 s su un arco di cerchio di raggio R = 10 m.

Al tempo t = 0 il pendolo si trova con velocità nulla nella posizione s(A) = s_A = 1 m , corrispondente all' angolo θ_A .

Calcolare quanto valgono le seguenti quantità:

La pulsazione ω del moto.

L'ampiezza angolare θ_A del moto (in radianti).

La velocità angolare massima   [dθ(t)/dt]_max del moto.

L' accelerazione angolare massima a_(max) del moto.

L' accelerazione centripeta, massima a_c(max) del moto.

R.: 2·π rad/s ; 0,1 rad ; 0,628 rad/s ; 3,9 rad/s² ; 3,9 rad/s² ;

Esercizio n. 28

Consideriamo un pendolo di lunghezza 10 m e massa 1,2 kg.

Esso, all’istante t = 0 , transita alla velocità di (√2)/2 m/s per un punto C che forma un angolo θ_c = (√2)/20 rad con la verticale. Determinare:

L’equazione oraria del pendolo;

Il tempo che impiega per giungere da C ad A, punto di massima elongazione;

La velocità e l’accelerazione quando la massa transita per la posizione di equilibrio.

R.: cos (t –π/4) m ; π/4 s ; 1 m/s ; 0.1 m/s² ; (valore di g = 10 m/s²)

Esercizio n. 29

Un uomo sta sul tetto di un edificio e lancia un grave verticalmente verso l’alto con una velocità di 12 m/s; il grave tocca il suolo dopo 4 s.

Calcolare:

La massima quota raggiunta.

L’altezza dell’edificio.

La velocità finale (altezze calcolate rispetto al suolo).

R.: 39,2 m ; 32 m ; 28 m/s verso il basso ; (assumere g = 10 m/s²)

Esercizio n. 30

Una sonda è lasciata cadere in un lago da una piattaforma posta 5 m sull’acqua.

Essa colpisce l’acqua con una certa velocità e raggiunge il fondo con la stessa velocità 5 s dopo che è stata lanciata. Calcolare:

Quanto è profondo il lago.

Si supponga di aspirare tutta l’acqua del lago, con quale velocità iniziale deve essere lanciata la sonda dalla piattaforma per toccare il fondo in 5 s?

R.: 40 m ; 16 m/s verso l’alto ; (assumere g = 10 m/s²)

Esercizio n. 31

Una particella si muove di moto armonico lineare attorno al punto x = 0.

All’istante t = 0 lo spostamento è x = 0,3 cm e la velocità è nulla.

Se la frequenza del moto è 0,25 Hz, determinare:

a)  Il periodo.

b)  Lo spostamento e la velocità in funzione del tempo.

c)  La velocità e l’accelerazione massime e gli istanti in cui sono massime.

R.: a) 4 s ; b) 0,3·cos(π·t/2) cm , – 0,15·cos(π·t/2) cm/s ; c) 0,47 cm/s , 0,74 cm/s² , (3·π/2+2·n·π) s ;  (π+2·n·π) s ;

Esercizio n. 32

Scrivere l’ equazione di un moto oscillatorio armonico se l’accelerazione massima del punto è 49,3 cm/s² , il periodo di oscillazione è T = 2 s e lo spostamento del punto dalla posizione di equilibrio all’istante iniziale è x_o = 23 mm.

R.: x(t) = 5·sen (π·t+0,48) cm ; x(t) = 5·sen (π·t+2,66) cm ;

Esercizio n. 33

L’orbita della luna attorno alla terra è approssimativamente circolare con un raggio medio di 3,84·10⁸ m.

Il periodo di rivoluzione è 27,3 giorni.

Trovare la velocità orbitale media e la sua accelerazione centripeta.

Trovare le stesse grandezze per il moto di rivoluzione della terra attorno al sole (raggio medio 1,5·10⁸ km, periodo 365 giorni).

R.: 1000 m/s ; 0,0026 m/s² ; 3·10⁴ m/s ; 0,0060 m/s² ;

Esercizio n. 34

Con quale velocità deve essere lanciata verso l’alto un oggetto per poter salire fino a 50 m. Per quanto tempo resterà in aria?

R.: 31,3 m/s ; 6,4 s ;

Esercizio n. 35

Un disco ruota con velocità angolare uniforme, facendo 33 giri/min.

A distanza r = 30 cm dal centro del disco si trova uno scarafaggio, fermo sul disco.

a)  Trovare l’accelerazione a cui è soggetto lo scarafaggio.

b)  Calcolare inoltre l’accelerazione se lo scarafaggio sta camminando con velocità uniforme (rispetto al disco) v = 10 cm/s in direzione radiale verso l’esterno.

R.: – 3,58 r ; – 3,58 r + 0,69 t m/s ;

Esercizio n. 36

Una ruota di raggio r rotola senza strisciare su un piano orizzontale con moto uniforme, il suo centro quindi ha una velocità costante v.

Esprimere le equazioni di un punto della periferia della ruota.

Esprimere le equazioni di un punto all’interno della ruota.

R.: [r ∙ (θ – sen θ) , r ∙ (1 – cos θ)] ; [(r ∙ θ – h ∙ sen θ) , (r – h ∙ cos θ)] ;

Esercizio n. 37

Un treno affrontando una curva rallenta da 90 km/h a 50 km/h nei 15 s che impiega a completare la curva.

Il raggio della curva è 150 m.

Calcolare l’accelerazione nel momento in cui la velocità del treno è 50 km/h, assumendo che in questo momento continui a decelerare.

R.: 1,48 m/s² , 29,9° ;

Esercizio n. 38

Un’automobile è parcheggiata su di una costa inclinata che sovrasta l’oceano, ad una inclinazione di 37° rispetto all’orizzontale.

Il conducente negligente lascia la macchina senza marcia innestata ed il freno a mano è difettoso.

La macchina parte dalla quiete giù per la discesa con un’accelerazione costante di 4,00 m/s² e percorre 50,0 m per raggiungere il bordo dell’altura. Questa è a 30 m al di sopra dell’oceano.

a)  Trovare:La velocità dell’automobile quando raggiunge il bordo dell’altura ed il tempo che impiega ad arrivare lì.

b)  La velocità dell’automobile quando arriva a livello dell’oceano.

c)  Il tempo totale in cui l’automobile è in movimento.

d)  La posizione dell’automobile rispetto alla base dell’altura quando l’automobile arriva a livello dell’oceano.

R.: 20 m/s ; 27,1 m/s ; 6,54 s ; 24,6 m ;

Esercizio n. 39

Uno sciatore vuole lanciarsi da un trampolino il cui ultimo tratto è un arco di circonferenza di apertura 60° e raggio R = 15 m. Trascurando la resistenza dell’aria e gli attriti, calcolare la velocità dello sciatore nel momento in cui lascia il trampolino (punto B) e l’altezza H dalla quale dovrebbe scivolare per raggiungere, partendo da fermo, un’altezza massima h = 12 m dopo aver lasciato il trampolino.

R.: 28 m/s : 42 m ;

Esercizio n. 40

Un punto materiale si muove lungo una circonferenza con legge oraria s(t) = B·t + C·t² , con B = –2 m/s e C = 1 m/s².

L’accelerazione del punto è, in modulo, 4,47 m/s² dopo 3 s.

Trovare il raggio della circonferenza.

R.: 4 m ;

Esercizio n. 41

Due treni che viaggiano uno a 72 km/h e l’altro a 144 km/h, sono diretti uno contro l’altro su un binario rettilineo in piano.

Quando si trovano a 950 m di distanza, ciascun macchinista vede l’altro treno e si affretta a frenare.

Verificate se avviene lo scontro nel caso in cui entrambi i treni rallentino con accelerazione, in modulo, di 1 m/s².

Se avviene, calcolate la velocità allo scontro, altrimenti la distanza tra i treni arrestati.

R.: si ; 0 m/s ; 10 m/s ;

Esercizio n. 42

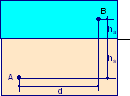
Su di una spiaggia un bagnino posto in A deve salvare un bagnante in pericolo posto in B. Le posizioni dei punti A e B sono riportate in figura e valgono: d = 40 m, h_s = 20 m ed h_a = 10 m. Determinare, tra tutti i percorsi possibili quello che richieda il minor tempo di intervento, supponendo che il bagnino corra con velocità costante v_s = 2 m/s sulla sabbia e con velocità v_a = 1 m/s in acqua.

R.: 31,34 s ;

Esercizio n. 43

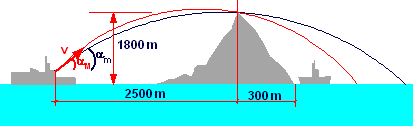
Una nave nemica è sulla riva est di un’isola montagnosa. La nave nemica può manovrare entro 2500 m dalla cima della montagna alta 1800 m e può sparare proiettili con una velocità iniziale di 250 m/s. Se la riva occidentale è a 300 m orizzontalmente dal picco, quali sono le distanze dalla spiaggia ad ovest alle quali una nave può essere al sicuro dai lanci della nave nemica?
 

R.: <270 m ; >3,48 km ;

Esercizio n. 44

Un corpo di massa 10,0 Kg, sottoposto alla forza di gravità, effettua una traiettoria descritta dalla funzione

y = −3·x² + 15,0·x + 36,0 , dove le coordinate del corpo sono espresse in metri.

Calcolare il modulo della velocità iniziale (quando x = 0).

R.: 19,2 m/s ;